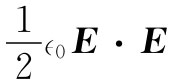）。当然，这里的u和S也许会依赖于势或其他的东西，但让我们看看能够算出什么结果来。可以尝试把E·j这个量重新写成为两项之和：其中一项是一个量的时间微商，而另一项则是第二个量的散度。这时，那第一个量该含u而第二个量则含S（带有适当符号），这两个量都必须只用场来表示的。这就是说，我们希望把上述方程写成假定存在仅仅取决于E和B的场能量密度u和能通量密度S，这是一种理念（例如，至少在静电学中就已知道，能量密度可以写成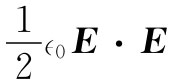
）。当然，这里的u和S也许会依赖于势或其他的东西，但让我们看看能够算出什么结果来。可以尝试把E·j这个量重新写成为两项之和：其中一项是一个量的时间微商，而另一项则是第二个量的散度。这时，那第一个量该含u而第二个量则含S（带有适当符号），这两个量都必须只用场来表示的。这就是说，我们希望把上述方程写成
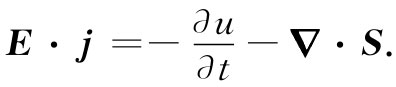（27.6）
左边应该首先仅仅用场来表示。我们如何能做到这一点呢？当然，要通过应用麦克斯韦方程组。根据关于B的旋度的那个麦克斯韦方程，用E对之点乘，便得
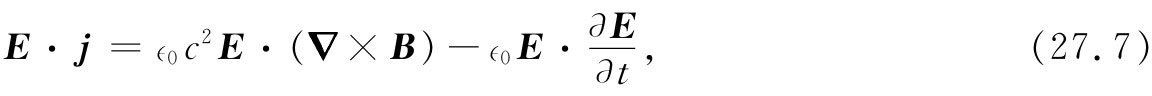
这样就已部分地完成了任务。最末一项是时间微商——即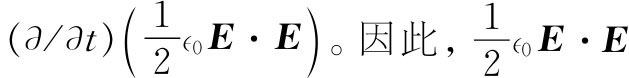
至少就是u的一部分了。这与我们曾经在静电学中求得的是相同的东西。现在，一切必须做的就是要使另一项纳入某种东西的散度之中。
注意式（27.7）右边的第一项与
（▽×B）·E （27.8）
相同。而正如你从矢量代数方面所知道的，（a×b）·c与a·（b×c）一样，因而上面这一项也就等同于
▽·（B×E）， （27.9）
这就有了“某种东西”的散度，这恰恰就是我们所需要的。结果这件事却是错的！以前曾向你们警告过，▽虽然“像”矢量，但与矢量不“完全”相同。之所以不是矢量，是因为有一个来自微积分学方面的附加惯例 ：当一微分算符置于一乘积的前面时，它要对右边每个东西都进行运算。在式（27.7）中，▽只对B运算，而对E不运算。但在式（27.9）的那种形式中，按照正常惯例，▽应当对B和E两者都进行运算。所以并不是 同一回事。实际上，若我们算出▽·（B×E）的各部分，就能看出它等于E·（▽×B）再加上 某些其他的项。这很像当我们取代数中一个积的微商时所发生的那种情况。例如，
并不打算将▽·（B×E）的所有各部分都算出，仅愿意向你们指明一个对付这种问题十分有用的技巧，那就是允许你将矢量代数的法则全部运用到含有算符▽的表示式上去而又不会引起任何麻烦的一种技巧。这技巧就是要丢开——至少暂时是如此——关于微商算符对什么进行运算的微积分符号表示法则。你会看到，通常，各项的次序用于两个 单独的目的。一个目的是在运算方面，为使f（d/dx）g不同于g（d/dx）f；另一个目的则是在矢量方面，为使a×b不同于b×a。如果我们乐意，可以决定暂时放弃这个运算法则，不去说明微商要对右边每件东西都进行运算，而是来制订一种与所写下来的各项次序无关的新 的规则。于是我们就能巧妙地处理前后各项而用不着操心。
这里就是新的规则：用下脚标来表示微分算符对什么进行运算，这样前后次序 就没有什么意义了。假设令算符D代表∂/∂x，那么Df 就意味着仅对变量f取微商，于是
但如果我们有Df fg，则它指的是
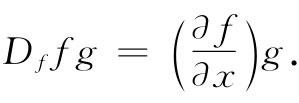
不过要注意，此刻按照我们的新规则，fDf g也意味着相同事情。我们可将相同的事情任意写成以下各种形式：
Df fg=gDf f=fDf g=fgDf .
你看，Df 甚至可以处在每件事情之后 （像这样一种方便的符号表示法竟从未在数学或物理学书中得到传授，真令人感到意外）。
你可能会怀疑：若我要 写出fg的微商，那该怎么办呢？我所要 的是对两 项的微商。那很容易，你只要这样说就行了，你写下Df （fg）+Dg （fg），而这恰好就是g（∂f/∂x）+f（∂g/∂x），也即在旧符号表示法中你用∂（fg）/∂x表示的意思。
你将会看到，现在算出关于▽·（B×E）的新表示式就变得很容易了。我们从改成新的符号表示法开始，也即写出
▽·（B×E）=▽B ·（B×E）+▽E ·（B×E）. （27.10）
当我们这样做时，就无需再保持次序上的正确了。我们始终懂得，▽E 只对E进行运算，而▽B 只对B运算。在这种场合下，就能够把▽当作通常的矢量那样来运用（当然，当运算结束时，就要回到每人常用的那种“标准”符号表示法上去）。因此，现在就可以做出像交换点积和叉积以及对各项进行其他类型的重新安排等各种事情。例如，式（27.10）中的中间项可以重新写成E·▽B ×B（你会记得，a·b×c=b·c×a），而那最末一项则与B·E×▽E 相同。这看来像是异想天开，但却没有什么问题。现在，如果我们试图回到通常的惯例上来，那必须安排得使▽仅对其“本身”的变量进行运算。第一项已经那样做了，因此可以仅仅去掉下标。第二项就需要某种调整才能使▽移至E之前，这我们可通过交换叉积的次序并改变符号而做到：
B·（E×▽E ）=-B·（▽E ×E）.
现在，式子已经按照惯常次序写出，因而就可回到通常的符号表示法上来。式（27.10）相当于
▽·（B×E）=E·（▽×B）-B·（▽×E） （27.11）
（在这一特殊情况下，较快的方法应该是一直利用各分量，但花点时间向你们指出这种数学技巧还是值得的。你或许将不会在其他地方见到它，但对于把矢量代数从关于含有微商的项的次序规则中解放出来是极为好用的）。
现在我们就回到能量守恒的讨论上来，并引用我们的新结果，即式（27.11），去变换式（27.7）中的▽×B项。这样，能量方程变成
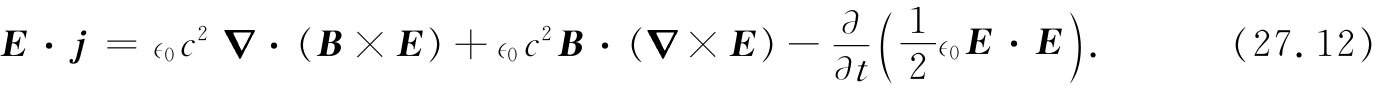
现在你看到，我们几乎完成任务了。这里有两项，一项用作u对于t的漂亮微商，另一项代表S的美妙散度。可惜，那中间项仍旧保留下来，它既不是散度，又不是对于t的微商，所以我们已经接近胜利，但还不完全。在经历了一番思考之后，回去查看麦克斯韦的微分方程组，幸运地发现▽×E等于-∂B/∂t，这就意味着我们可以把这独特项转变成单纯的时间微商：
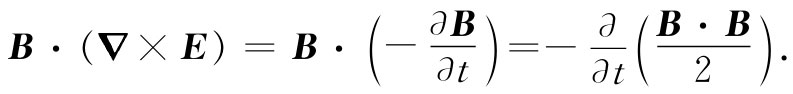
现在完全具有了我们所需要的一切。我们的能量方程可写成
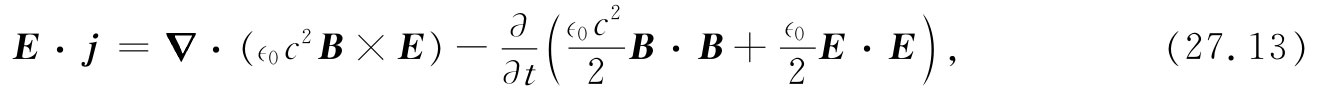
那就完全像式（27.6），只要下这样两个定义：
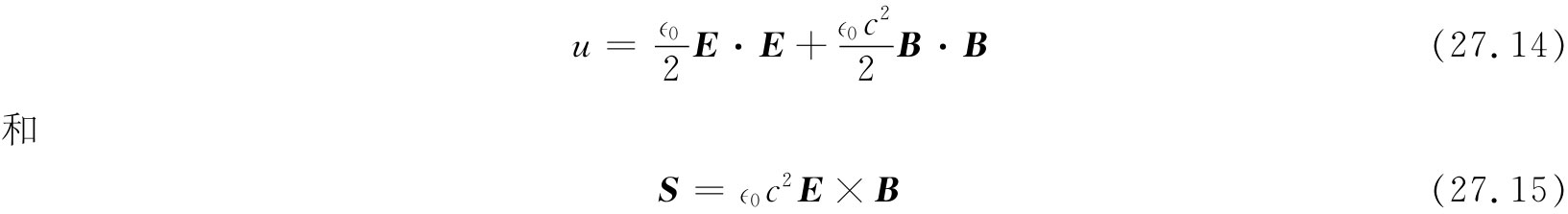
（交换叉积的次序使符号显得正确）。
我们的计划是成功的。已经有一个关于能量密度的表示式，它是“电”和“磁”两种能量密度之和，它们的形式很像以前我们在静场情况下求得的形式，那时我们计算出了用场表示的能量公式 。并且，我们也已找到了关于电磁场的能流矢量的公式。这一新的矢量，S=∈0 c2 E×B，按照它的发现者的名字，称为“坡印亭矢量”，它告诉我们有关场能在空间各处流动的速率，每秒流经一小面积da的能量为S·nda，其中n为垂直于da的单位矢量（现在你有了u和S的公式，若乐意的话，便可忘掉那些推导过程）。