图27-2 关于光波中的E,B和S矢量

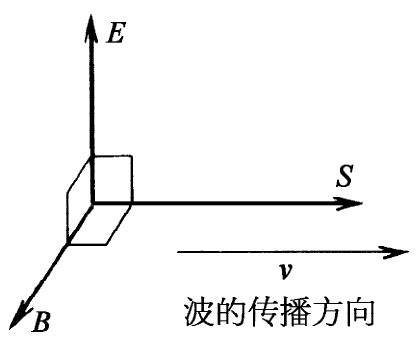
图27-2 关于光波中的E,B和S矢量
关于能流矢量S的公式,是某种相当新鲜的事情。我们现在就要来看看,在某些特殊情况下它是如何工作的,并看看它是否与以前已知的任何事情互相验证。我们将举的第一个例子是光。在一个光波中,E矢量和B矢量互相正交而且也垂直于波的传播方向(见图27-2)。在电磁波中,B的大小等于1/c乘上E的大小,而且由于它们互相垂直,所以还可写成
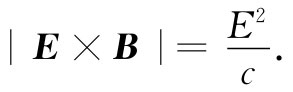
因此,对于光来说,每秒通过单位面积的能流为
S=∈0 cE2 (27.16)
在E=E0 cosω(t-x/c)的那种光波中,每单位面积能流的平均速率,即〈S〉平均 ——也称为光的强度——为电场平方的平均值乘以∈0 c:
强度=〈S〉平均 =∈0 c〈E2 〉平均 . (27.17)
信不信由你,我们曾在第1卷§31-5中学习光学时就已经导出过这一结果。应该可以相信这结果是正确的,因为它也被另外某些事情所核实。当我们有一光束时,在空间中就存在由式(27.14)所给出的能量密度。对于光波利用cB=E,得出
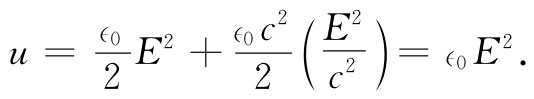
但E在空间中是变化着的,因而平均能量密度为
〈u〉平均 =∈0 〈E2 〉平均 . (27.18)
现在,波以速率c传播,所以应该想到每秒穿过一平方米的能量等于c乘以每立方米中的能量。因此我们会说
〈S〉平均 =∈0 c〈E2 〉平均 .
上式是对的,因为它与式(27.17)相同。
现在举出另一例子。这是相当奇妙的一个例子。我们来考察正在缓慢充电的电容器中的能流(并不要求那么高的频率,以致电容器初看起来像一个共振空腔,但也不要是直流电)。假定是用一个普通类型的圆形平行板电容器,如图27-3所示,在其内部有一个几乎均匀而随时间变化的电场。在任何时刻,这内部的总电磁能等于u乘以体积。若两板的半径均为a而其间隔为h,则在两板间的总能量为
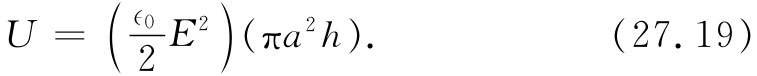
当E改变时,这个能量也在改变。当电容器充电时,位于两板间的体积正在以速率

接受能量。因此,一定会有从某处进入该体积中的能流。当然,你知道,它必定从那些用作充电的导线进来——但完全不是这样!它不可能经由该方向流入两板内的空间,因为E是与板垂直的,所以E×B就一定与两板平行 。
当然,你会记得,当电容器正在充电时,就有一个环绕轴的圆形磁场。我们在第23章中对此曾有所讨论。利用麦克斯韦方程组中最后一个方程,已求得在电容器边缘上磁场由下式给出:

它的方向如图27-3所示。因此,就有一个正比于E×B的能流从边缘四周进入,如图中所示。能量实际上并不是从导线下来的,而是从围绕着该电容器的空间那里来的。
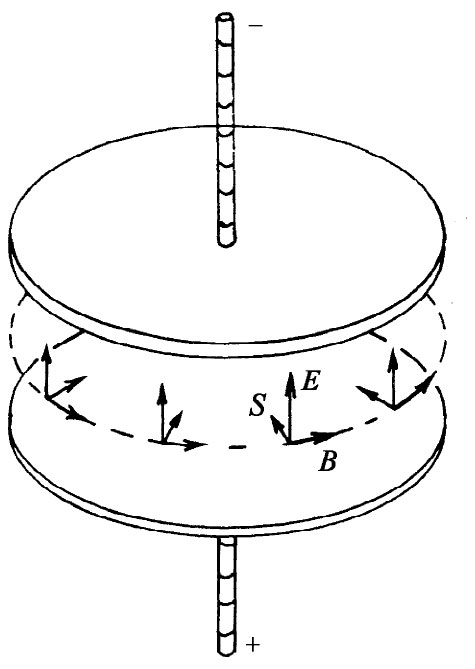
图27-3 接近一个正在充电的电容器,坡印亭矢量S会朝轴心指向内
让我们来核对一下通过两板边缘间的整个面的总能流是否与其内部能量的变化率相符——看来这样较好。为了核实,虽然我们仔细研究了证明式(27.15)的工作的全过程,但还是让我们来弄弄清楚。该面面积为2πah,而S=∈0 c2 E×B的量值为
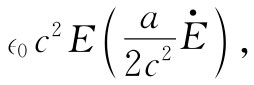
因此总能流为
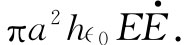
这的确与式(27.20)相符。但它告诉我们一件奇怪的事情:当对电容器充电时,能量并不是沿导线下来的,而是穿过边缘的间隙进来的。那分明就是这一理论所说的!
怎么能够是这样的呢?这虽不是 一个容易解决的问题,但这里有一个考虑该问题的方法。假设在该电容器的上面和下面很远处都有一些电荷,当电荷离得很远时,就会有一个微弱的但却是极其散开的场包围着该电容器(见图27-4)。于是,当这些电荷靠拢时,离电容器较近处的场就变得较强。因此,远处的场能量是会朝该电容器移动过来并最后停驻于两板之间。
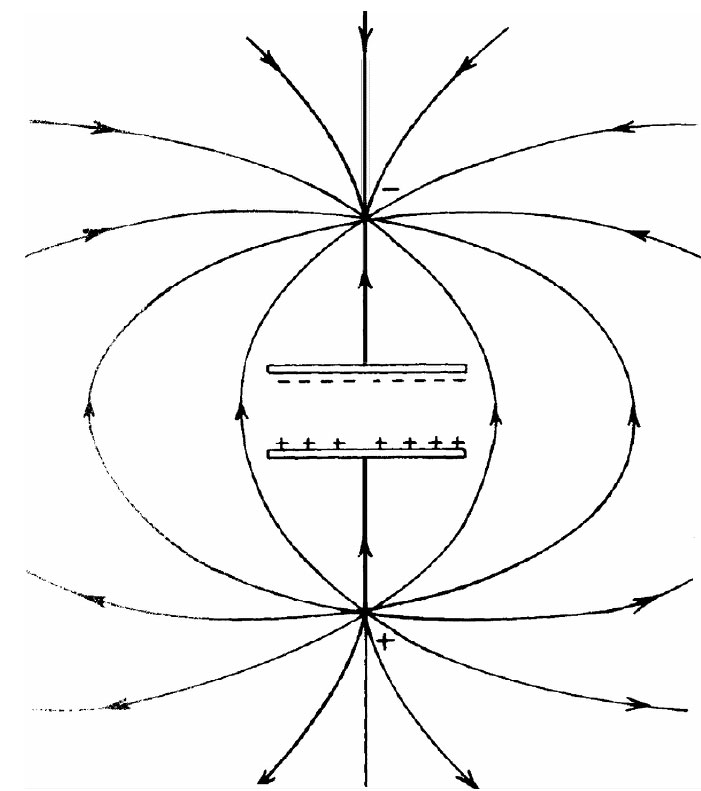
图27-4 当将两电荷从远处移来对一电容器充电时,在电容器外面的场
作为另一个例子,试问在一根有电阻的导线中当它载有电流时会有什么情况发生。既然这根导线中有电阻,则沿导线方向便有驱动电流的电场。由于沿导线有电势降,因而刚好在导线外面存在与其表面平行的电场(见图27-5)。此外,还有一个由电流所产生的环绕着导线的磁场。E和B成直角,因此就有一个沿半径而指向内的坡印亭矢量,如图中所示,即有一个从周围各处流进导线的能流。当然,这等于导线中以热的形式损耗掉的能量。因此,我们的“狂妄”理论讲:由于能量从外面的场流进了导线,电子才获得它们用以产生热的那些能量。直觉似乎告诉我们,电子是由于沿着导线被推动才获得能量的,因而这能量应该是沿导线流下(或流上)。但这一理论却说:电子实际上是被来自远处的某些电荷的电场所推动的,而它们从这些场获得了产生热的能量。能量总会莫明其妙地从遥远处的电荷流进空间的广阔区域,然后又流进导线中去。
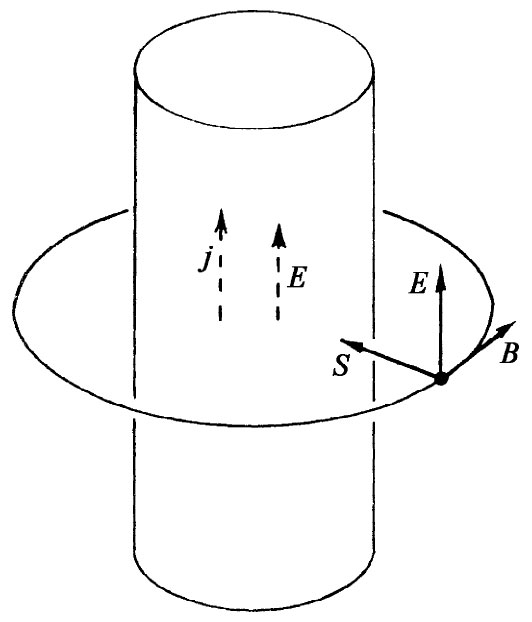
图27-5 在一根载流导线附近的坡印亭矢量S
最后,为了使你确实相信这一理论明显是一个难题,我们将再举一个例子——其中有一电荷和一块磁铁彼此都静止 地互相靠近着的例子——即两者都固定不动。假设取一个其中的点电荷被置于棒状磁铁中点附近,如图27-6所示。每一件东西都是静止的,从而能量并不会随时间变化。而且,E和B也都是完全静止的。可是坡印亭矢量却说存在一个能流,因为E×B并不等于零。如果你考察这能流,就会发现它不过是在一圈圈地循环旋转。任何一处都没有能量方面的任何变化——凡是流进某一体积里的东西都会从那里再流出来。这很像不可压缩的水在环流。因此,在这种所谓静态的情况下还存在能量的环流。这是多么荒谬!
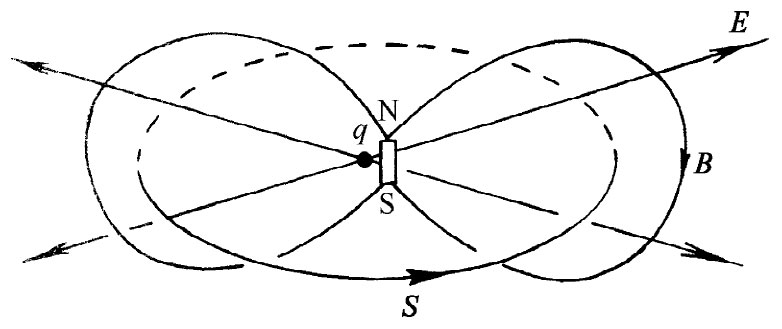
图27-6 电荷和磁铁会产生一个绕闭合回路循环的坡印亭矢量
然而,当你记起我们所谓的“静”磁实际上是一种环行的永久电流时,这也许就不会使你那么可怕地感到莫明其妙。在一块永磁体中,其内部电子都在永恒地旋转。这样也许能量在外面环流这一点就不那么奇怪了。
你无疑开始得到这么一个印象,即坡印亭理论至少部分地违背了你对于在电磁场中能量被设置于何处的那种直觉。你也许会相信,必须对你的一切直觉都进行修改,因此在这里有许多东西得学习。但实际上似乎并不需要。如果有时忘记了导线里能量是从外面流进来而不是沿导线传来的,但你无需感觉到,你就会陷入巨大的困难。在应用能量守恒的概念时,过细地注意能量所取的路径,看来好像价值不大。能量围绕着一块磁铁和一个电荷在兜圈子,这在大多数场合似乎是很不重要的。它并非一个极为重要的细节,但很清楚,我们通常的直觉却是很错误的。