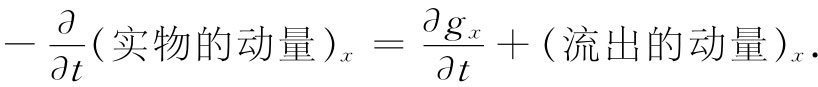
接下来,我们希望谈论关于电磁场中的动量 。正如场具有能量一样,它的每个单位体积也将具有一定的动量。让我们称之为动量密度g。当然,动量具有各种可能的方向,因而g必定是个矢量。让我们每次谈一个分量,首先,考虑x分量。由于动量的每一分量都守恒,所以可能写下一个看来有点像这样的定律:
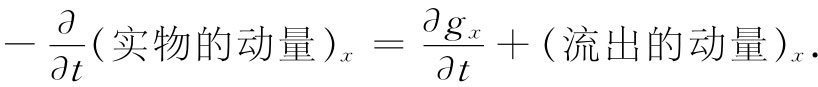
左边是容易理解的,实物动量的变化率正好就是作用于其上的力。对于一个粒子来说,这力就是F=q(E+v×B),对于一个电荷分布来说,则作用于单位体积上的力为(ρE+j×B)。然而,“流出的动量”这项却有点奇怪。它不可能是一个矢量的散度,因为它并非一个标量,其实是某一矢量的x分量。无论如何,它看来大概有点像
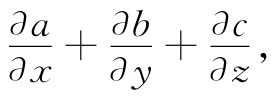
因为x动量还可能在三个方向中的任意一个方向上流动。总之,不管a,b和c是什么,这个组合被认为等于x动量的流出量。
现在这场游戏应该是仅仅用E和B来写出ρE+j×B,利用麦克斯韦方程组而把ρ和j消掉,然后才对那些项调整并做一些代换以使它看来像如下的形式:
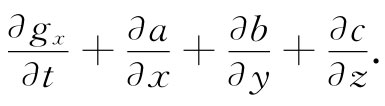
之后,通过对那些项做出标记,就会得到关于gx ,a,b和c的表示式。它的工作量很大,我们并不打算那样做,而只准备找出关于动量密度g的表示式——而且是通过另一种方法来求的。
在力学中有一个重要定理,这就是:在任何场合下,每当真正存在能量(场能或任何其他类型的能量)流动时,则单位时间流经单位面积的能量,乘以1/c2 ,就等于空间内单位体积的动量。在电动力学的特殊情况下,这一定理给出了g等于1/c2 乘以坡印亭矢量的结果:
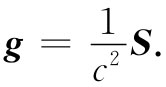 (27.21)
(27.21)
因此,坡印亭矢量不但会给出能流,而且只要除以c2 ,也就给出了动量密度。这同样的结果可从我们提出过的另一种分析方法获得,但更有意义的还是去注意这个更加普遍的结果。现在将提供若干有趣例子及论证以便使你们相信这个普遍定理是正确的。
第一个例子:假设在一个箱子里存在大量粒子——比方说每立方米中含有N个粒子——而它们以某个速度v运动着。现在就来考虑一个垂直于v的想象平面。每秒通过这个面单位面积的能流,等于每秒流过的粒子数Nv乘以每一粒子所带的能量。因每个粒子的能量为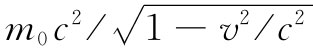 ,所以每秒的能流就是
,所以每秒的能流就是
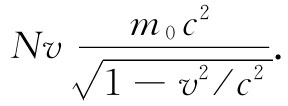
但每个粒子具有的动量为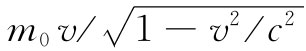 ,因而动量密度
为
,因而动量密度
为
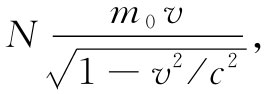
这恰好就是1/c2 乘以能流——和该定理所说的相同。因此,对于一群粒子来说这定理是正确的。
这定理对于光来说也正确。我们过去在第1卷学习光学时就曾看到,当从一束光吸收能量时,会有一定动量递交给该吸收体。事实上,在第1卷第34章中我们曾经证明,动量等于1/c乘以所吸收的能量[第1卷的式(34.24)]。若令U0 代表每秒到达单位面积的能量,则每秒到达单位面积上的动量就是U0 /c。但动量以速率c传播,因而在该吸收体前面的动量密度 就必然是U0 /c2 。因此,再次表明该定理是对的。
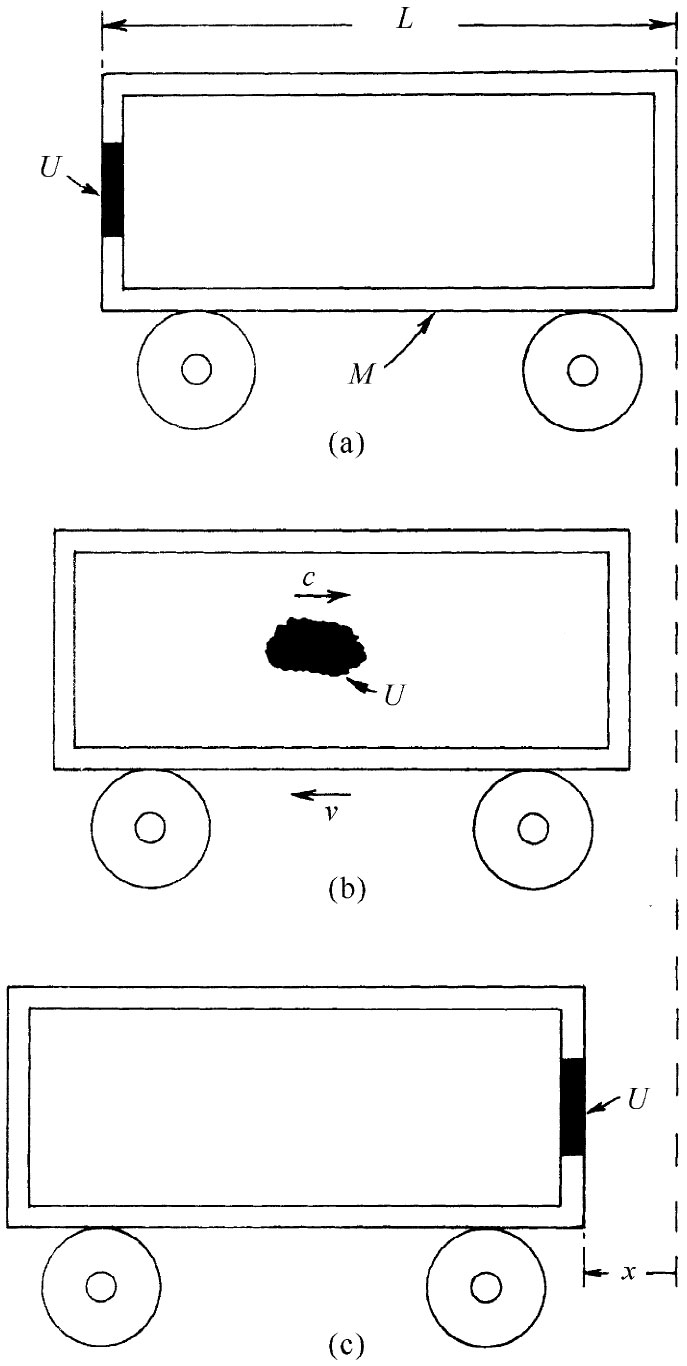
图27-7 以速率c运动着的能量U会带有动量U/c
最后,我们将提供一个论据,这论据来源于爱因斯坦对同样事情的又一次证明。假设有一火车车厢在轨道上自由滑动(假定没有摩擦阻力),这车厢具有某巨大质量M。车厢里的一端配有能发射出一些粒子或光(或任何其他东西,到底是哪一种东西都没有什么区别)的某种装备,然后这射出来的东西就给车厢对面一端所截住了。原来有某些能量放在车厢的一端——比如说是图27-7(a)中所标明的能量U——而后来它却转移到了对面的一端,如图27-7(c)所示。这能量U已经移动了一个等于该车厢长度的距离L。既然能量U具有质量U/c2 ,因而要是车厢保持不动的话,该车厢的重心就必然会移动。爱因斯坦不喜欢一物体的重心可以只凭在其内部瞎胡闹一番就能使其移动的那种想法,因而他假定通过在物体内部做任何事情来移动其重心是不可能的。但如果事实确是那样,则当我们把能量U从一端移至另一端时,整个车厢就应反冲一段距离x,如图(c)中所示的。实际上,你可以看到,车厢的总质量乘以x就必定等于所移动能量的质量U/c2 乘以L(假定U/c2 比M要小得多):
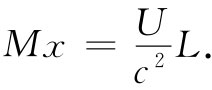 (27.22)
(27.22)
现在让我们来考察一下能量由一次闪光所携带的那种特殊情况(该设备也同样适用于粒子,但我们将跟随爱因斯坦,他对于光的问题感兴趣)。究竟是什么东西会引起车厢移动的呢?爱因斯坦这样议论说:当光被发射出来时一定存在反冲,即带有动量p的某个未知的反冲。正是这一个反冲才使车厢向后滚动的。车厢的反冲速度v等于这一动量除以车厢质量:
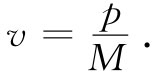
车厢以这一速度运动,直至光的能量到达对面一端为止。于是,当它碰到时,它交还了它的动量而使车厢停住了。如果x很小,则车厢运动的时间约等于L/c,所以就有
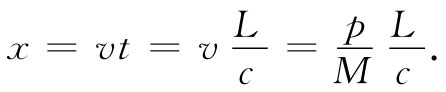
把这个x值代入式(27.22)中,便得
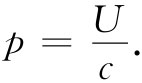
我们又一次得到了光的能量与动量的关系。用c相除则获得动量密度g=p/c,因而又得到
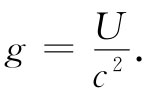 (27.23)
(27.23)
你可能会觉得奇怪:为什么重心定理会那么重要?也许它 是错的。或许是吧,但那时我们也可能丧失角动量守恒律。假定我们的车厢沿着轨道以某一速率v前进,而同时我们把某些光能从车顶 射向车底 ——比方说,从图27-8中的A点射至B点。现在来考察这系统相对P点的角动量。能量U在离开A点之前,它具有质量U/c2 和速度v,从而具有角动量mvrA 。当它到达B点时,仍具有相同的质量,而倘若整个车厢的线 动量不会发生变化,则它必定仍具有速度v。这时它相对P点的角动量就是mvrB 。这角动量将会改变,除非 当光被射出时正确的反冲动量曾给于车厢——也就是说,除非光携带动量U/c。结果变成,角动量守恒与重心定理在相对论中是紧密相联的。因此,要是我们的重心定理不正确,则角动量守恒就被破坏了。无论如何,已经弄清楚它是一个正确的普遍定律,而在电动力学的情况下我们还能利用它来获得场的动量。
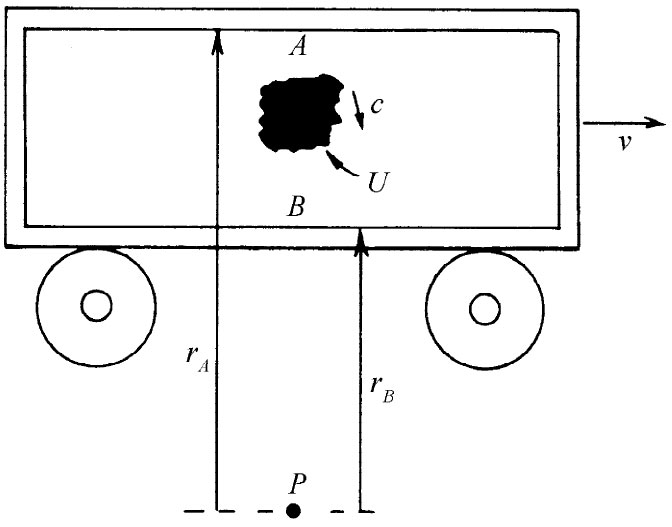
图27-8 如果环绕P点的角动量是守恒的,则能量U应带有动量U/c
我们将进一步提及在电磁场中关于动量的两个例子。曾在§26-2中指出,当两个带电粒子在互成直角的轨道上运动时作用与反作用定律失败了。作用于两粒子上的力并不平衡,因而作用并不等于反作用,这样实物的净动量就必然正在改变,它是不守恒的。但在这样一种情况下场的动量也正在改变。如果你算出由坡印亭矢量所给出的动量,则它不是一个常数。然而,粒子动量的改变刚好被这个场的动量所抵偿,所以粒子加上场的总动量守恒。
最后,另一个例子则是如图27-6所示的具有磁铁与电荷的那种情况。我们曾由于发现有能量处处绕圆周流动而感到不快,但此刻,由于我们知道能流与动量是互成比例的,所以我们也知道在空间有环行着的动量。可是一个环行 动量就意味着存在角动量,因此在场中有角 动量。你是否记得,在§17-4中我们描述过的关于放在圆盘上的一个螺线管和若干个电荷的那个佯谬?似乎当电流中断时,整个盘会开始旋转。令人迷惑的是:角动量到底是从哪里来的?答案:如果你有一磁场和某些电荷,则在场中就会有某一角动量。当场建立时,它必定已经安置在那里了。而当场去掉时,这一角动量被还了回来。因此在该佯谬中的盘子就应该 开始转动。这一神秘的能量环流,最初似乎觉得是那么荒谬可笑,但却是绝对必需的。确实有一个动量流,为了在整个世界中保持角动量守恒,它是必需的。