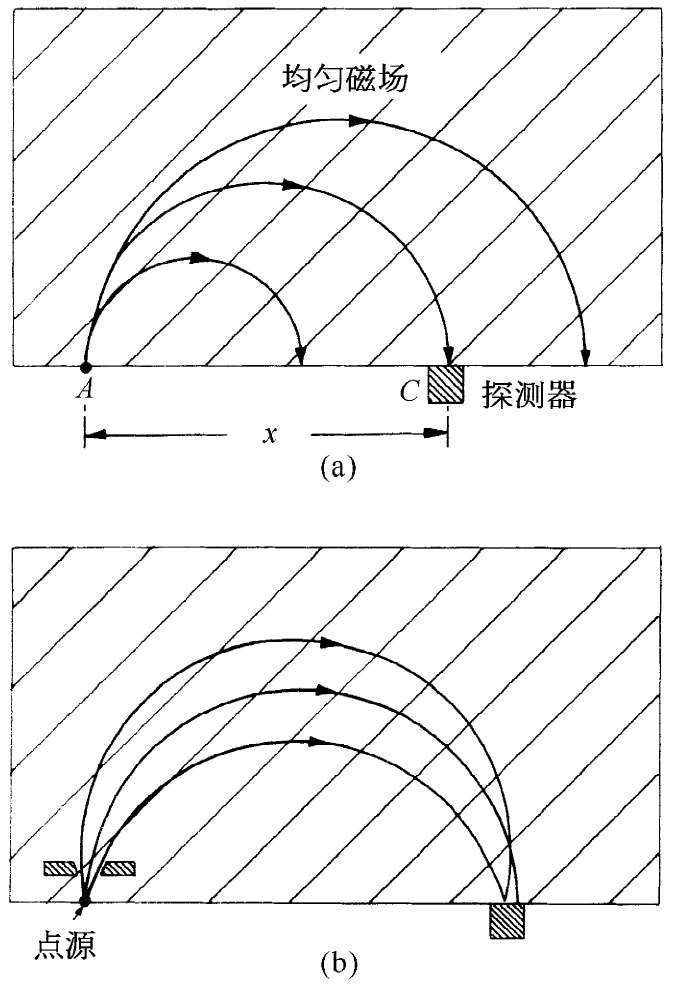
一个匀强磁场往往被用来制造一台高能带电粒子的“动量分析器”或“动量谱仪”。假定带电粒子在图29-2(a)中的A点被射入一匀强磁场,这磁场与该图面垂直。每个粒子将在半径正比于该粒子动量的一个圆周上运动。如果所有粒子都与场边缘正交地进入场中,那么它们将在一个离A点距离为x的地方离开场,这x值正比于它们的动量p。位于诸如某点C的计数器将只能探测到动量p=qBx/2附近间隔Δp内的那些粒子。

图29-2 匀强磁场,180°聚焦的动量谱仪:(a)动量不同;(b)角度不同(磁场方向与图面垂直)
当然,并不要求粒子在它们被探测到之前都要走过180°,但这种名为“180°谱仪”却具有一种独特性质,并不一定要求所有粒子全都与场的边缘成直角进入场中。图29-2(b)显示三个粒子的轨道,它们都拥有相同的 动量,但以不同角度进入场中。你看到它们各取不同轨道,可是全都在很靠近于C点处离开了场。我们说存在一个“焦点”。这种聚焦特性有其优越之处,即在A点有较大角度的粒子也可以被接收到——虽然往往得强加上某些限制,如图中所示。对一个较大角度范围的接收经常意味着较多的粒子在给定时间内被计算了进去,这就减少了对给定的测量所需的时间。
通过变更磁场,或沿x轴移动计数器,或由运用许多个计数器覆盖x的一个范围,入射束的动量“谱”就可以被测得了[所谓“动量谱”f(p),我们指的是动量在p与(p+dp)之间的粒子数为f(p)dp]。比方,这样的方法曾用来测定各种原子核在β衰变中的能量分布。
有许多其他形式的动量谱仪,但我们将只描述具有特别大接收立体 角的那一种。它是以如图29-1所示的那种在均匀强场中的螺旋轨道为基础的。让我们设想一个柱面坐标系ρ,θ,z,使得z轴沿着场的方向。如果粒子相对于z轴以某一角度α从原点射出,则它将沿方程为
ρ=asinkz,θ=bz
的螺旋线运动,其中a,b和k都是你可以容易用p,α和磁场B来表示的参数。如果对于给定的动量,但对于几个不同起始角,把与轴的距离ρ作为z的函数画成曲线,则我们将得到像图29-3所示的那些实曲线(记住这不过是对一条螺旋形轨道的投影)。当入射方向与轴成较大角度时,ρ的峰值变大,但其纵向速度则变小,从而使不同角度的轨道趋向于在图的A点附近形成一个“焦点”。如果我们放置一个窄孔于A处,那么在一个起始角范围内的粒子仍然能够全部到达并穿过窄孔到达z轴,在那里粒子可由一个长条形探测器D进行算数。
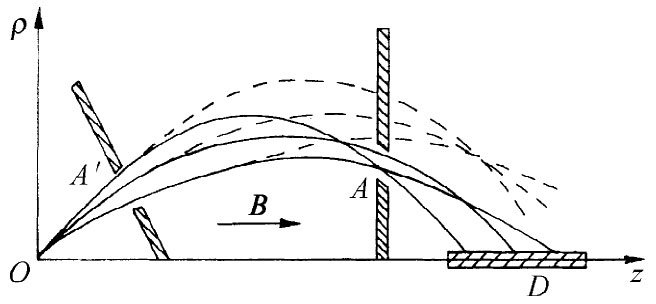
图29-3 一个轴向场式谱仪
以较大的动量但以相同的角度从原点处的源射出的粒子,将遵循图中所示虚线轨道运动而不能穿过A处的窄孔。因此,这台仪器将选出一个小间隔的动量。与上述第一种谱仪相比它的优点是:孔A以及孔A′都可以做成环形孔,以便使在一个相当大的立体角范围内离开了源的粒子都能够被接收到。来自源的大部分粒子都给应用上了——对于弱源或对于十分精密的测量这都是一个重要优点。
然而,人们为这个优点付出了代价,因为这样做需要一个大体积的匀强磁场,而这往往仅对低能粒子才是切实可行的。你会记得,制造匀强磁场的一种办法是在球面上绕一个线圈,使得其面电流密度正比于角度的正弦。你也能够证明,这同样的事情对于一个旋转椭球来说也属正确。因此这种谱仪往往通过在一个木(或铝)架上绕一个椭球形线圈来制造,所要求的一切就是在每个轴线距离间隔Δx内的电流都相同,如图29-4所示。
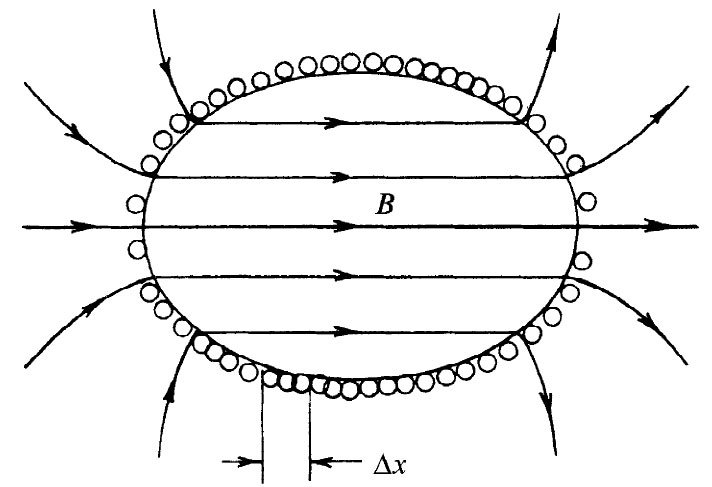
图29-4 每个轴线间隔Δx中有相等电流的椭球形线圈在其内部产生匀强磁场