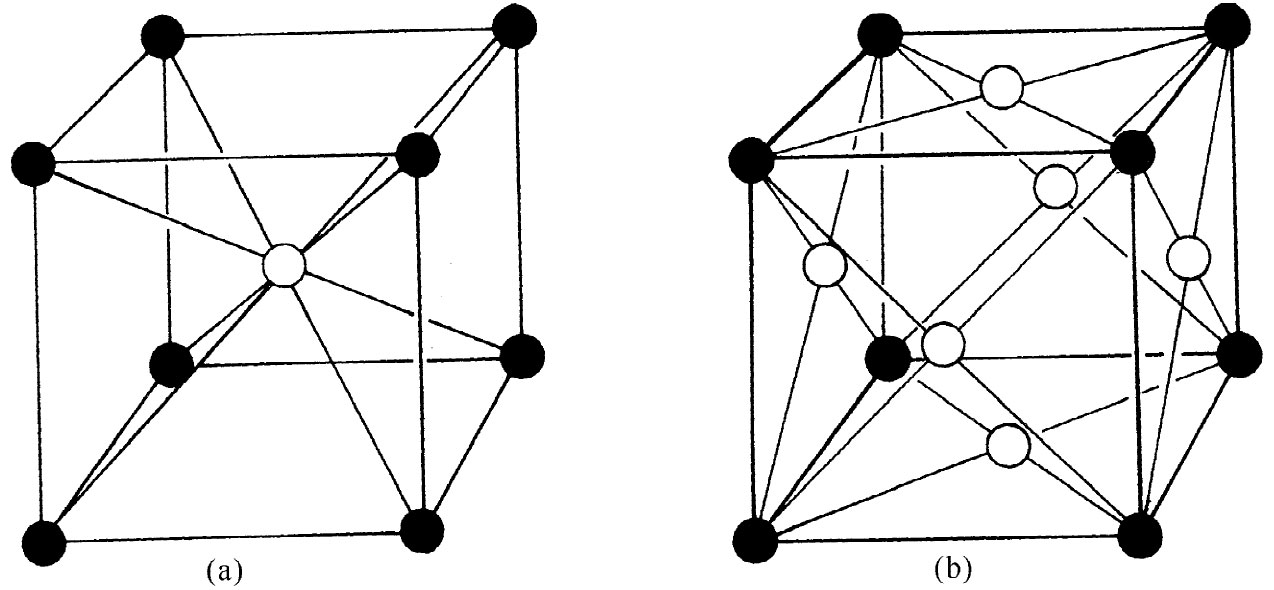
图30-4 立方晶体的晶胞:(a)体心立方;(b)面心立方
晶体中原子的排列——晶格——可以取许多种几何形态。我们愿意先来描述那些最简单的晶格,它们是大多数金属以及由惰性气体所形成的固体的特征。它们是能够以两种形式存在的立方晶格:如图30-4(a)所示的体心立方,与如图30-4(b)所示的面心立方。当然,图上所示的只是晶格中的一个立方,你得想象这种图样在三维中被无限地重复着。并且,为了使画面比较清楚,只表示了原子的中心。但在一实际晶体中,原子更像是互相接触着的球体。图中的实心球和空心球,一般说来,可以代表异类原子,也可代表同类原子。例如,铁在低温时具有体心立方晶格,但在高温时则形成面心立方晶格。在这两种结晶形态中其物理性质很不相同。

图30-4 立方晶体的晶胞:(a)体心立方;(b)面心立方
这样的形态是怎样得来的呢?试设想你有一个要把球形原子堆积成尽可能紧密的问题。一种办法可能是开始通过造成一个“六角密堆积排列”中的一层,如图30-5(a)所示。然后你就会建立与第一层相似的第二层,但在水平方向上作位移,如图30-5(b)所示。此后,你还可放上第三层。但要注意!安放第三 层有两种 显然不同的方式。若你通过放一个原子于图30-5(b)的A处而开始第三层,则这个第三层中的每一原子就正好位于底层的一个原子之上。另一方面,如果你通过放一个原子于位置B而开始第三层,则这个第三层的原子将恰恰被置在由底层的三个原子所形成的三角形的中心点上方。任何其他的初始位置都相当于A或B,从而就只有这两种安放第三层的方式。
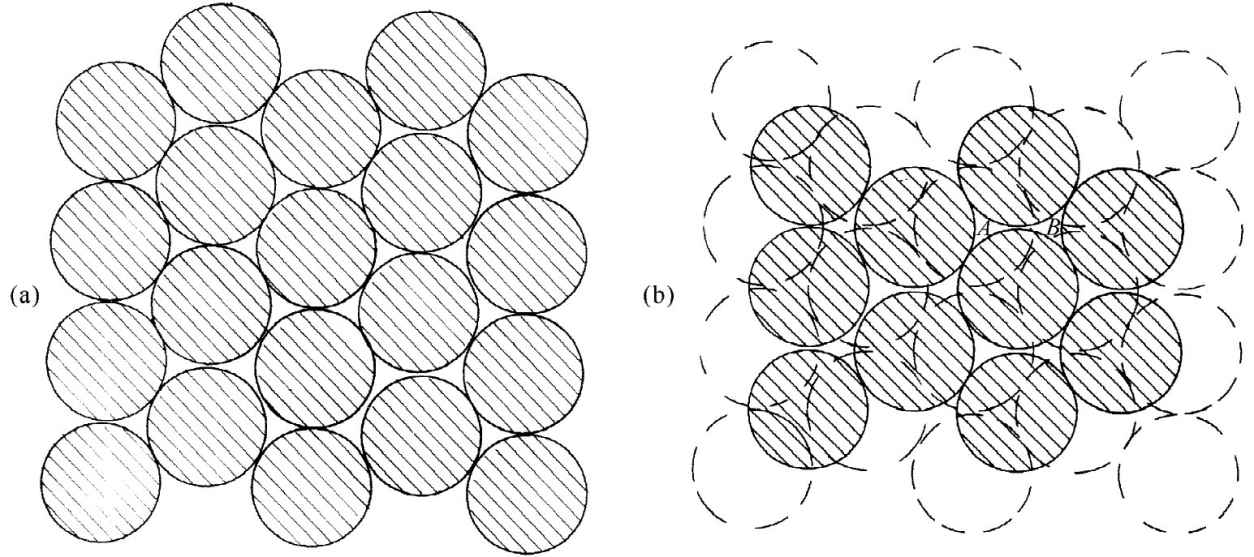
图30-5 建立一个六角密排点阵
如果第三层有一个原子位于B点,则这种晶格就是面心立方——不过是从一个角度去看。似乎很有趣,本来你是从一个六角形开始的,但到头来却得到一个立方体。可是要注意,若从角隅去看,一个立方体就会有六角形的轮廓。比方,图30-6就可以代表一个平面上的六角形或一个透视中的立方体!
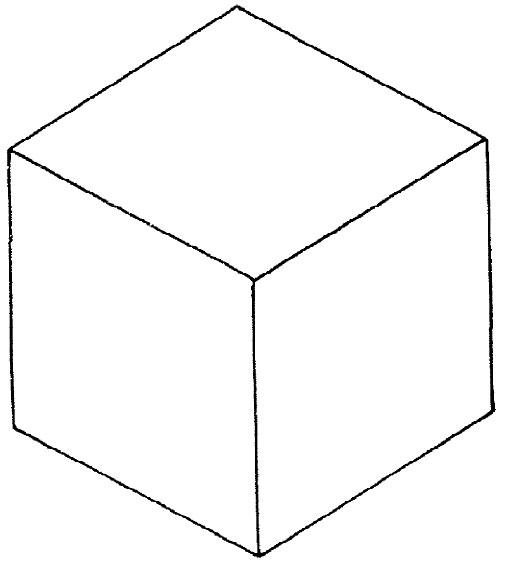
图30-6 从一个角上去看,这是个六角形还是个立方体?
如果第三层是通过把一个原子放在A点上而叠加于图30-5(b)上,则不会有立方结构,这个晶格此时只有六角对称。很清楚,我们刚才所述的这两种可能性都是属于密堆积。
某些金属——诸如铜和银——选择第一种可能性,即面心立方。其他——例如铍和镁——则选取另一种可能性,它们形成六角晶体。很明显,将出现哪一种晶格,不能仅仅取决于小球的堆积,也必须部分地由其他因素确定。特别是,这有赖于原子间作用力的少量剩余的角依存关系(或对于金属而言,则有赖于该电子海的能量)。你无疑会在化学课中学到所有这些东西。