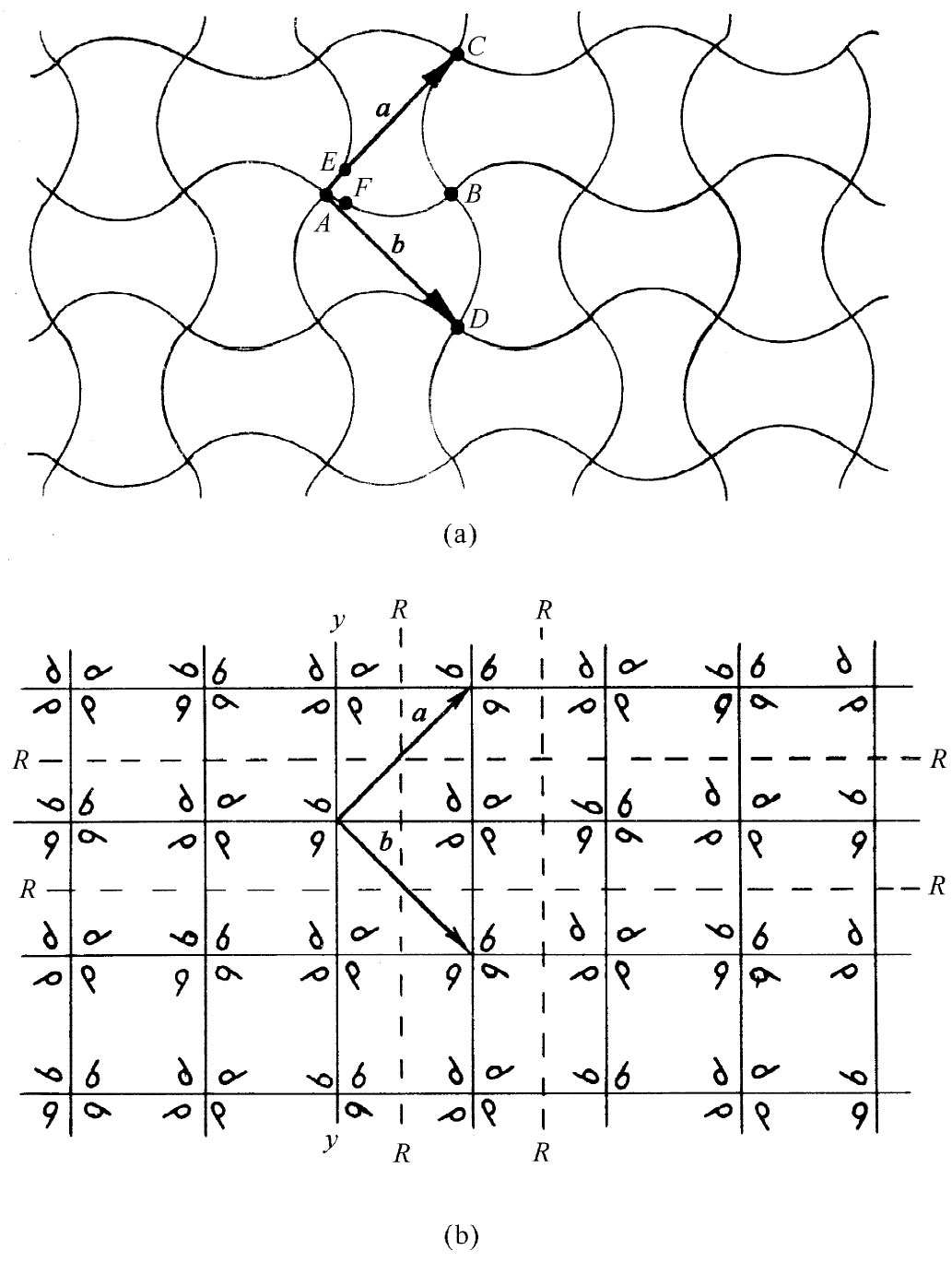
图30-7 一个高对称性的图样
我们现在愿意从内禀对称性的观点来讨论晶体的某些性质。晶体的一个主要特点是:若你从某一原子出发而移过一个晶格单位到达一个对应原子,则你将再处在同样一种环境中,这是基本命题。但假如你是一个原子,也许还有另一种变化能够把你再带到同样一种环境——这就是说,存在另一种可能的“对称性”。图30-7(a)显示另一种可能的“墙纸型”设计(虽则你可能从未见过)。假设我们要来比较A和B两点的环境。起初,你也许认为它们彼此相同——但又不完全相同。C和D两点与A是等效的,但B点的环境只有在经过了倒转,诸如在镜面中的反射,才会像A的环境。
在这一图样中还有其他类型的“等效”点。比如,点E和F,除了一点相对另一点转过90°之外,它们具有“相同”环境。这一图样很特别。环绕顶点诸如A旋转90°或90°的任一整数倍,会再给出一个完全相同的图样。一块具有这种结构的晶体在其外表看来该有正方的棱角,但其内部比简单立方稍微复杂。
现在已描述了某些特殊例子,让我们尝试算出晶体具有的一切可能的对称性。首先,我们考虑在一个平面上发生的情况。一个平面 晶格可以通过两个所谓基矢 来定义,这两个矢量是从晶格中的一点指向两个最邻近 的等效点的。图30-1中那两个矢量1和2就是该晶格的基矢。图30-7(a)中的a和b两矢量则是那种图样的基矢。当然,我们尽可以用-a来代替a,或用-b来代替b的。由于a和b的大小相等并互相垂直,所以90°角的转动会将a变成b,并将b变成-a,这又给出相同的晶格。

图30-7 一个高对称性的图样
我们看到存在一些具有“四次”对称性的晶格,而前面则已描述了一种密堆积排列,它是以具有六次对称性的六角形为基础的。对于图30-5(a)中排列的圆圈,环绕任何一个圆心做一个60°角的转动将会把该图样转回到原来样子。
还有哪些其他类型的转动对称性呢?比方,能否有五次或八次转动对称性呢?很容易看出那是不可能的。多于四次的唯一一种对称性就是六次对称 。首先,让我们来证明多于六次的对称是不可能的。假设我们试图想象一种晶格,其中的两个等长初基矢做成小于60°的内角,如图30-8(a)所示。我们必须假定:B和C两点各等效于A,而a和b便是从A点至其等效邻点的两个最短 矢量。但这显然是错误的,因为在B与C两点间的距离比从其中任一点至A点的距离还要短。因此就必定有一个与A点等效的、而较B点或C点近的邻点D。我们本来就应当选取b′作为我们的初基矢之一,所以两个基矢所夹之角必然是60°或更大。八次对称根本没有可能。
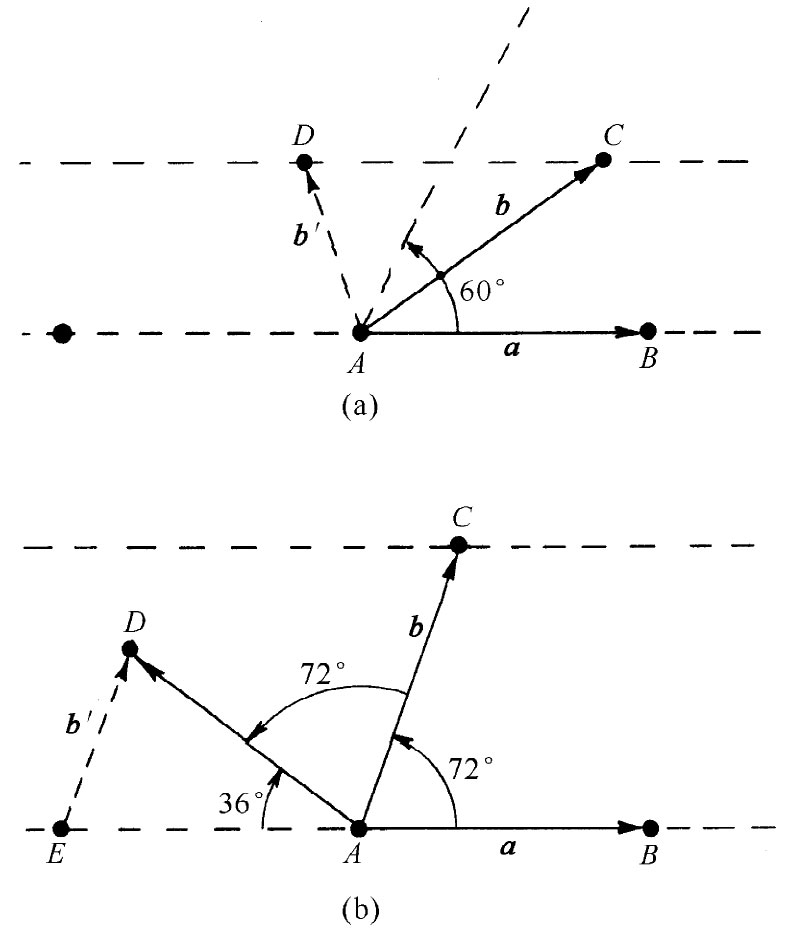
图30-8 (a)多于六次的转动对称是不可能的;(b)五次转动对称性也没有可能
关于五次对称又怎么样呢?若我们假定该初基矢a和b具有相等长度,并且做成一个等于2π/5=72°的角度,如图30-8(b)所示,那么在D处也就应有一个等效格点与C作成72°角。但此时从E至D的矢量b′比b短,因而b就不是一个初基矢了,这样五次对称就不可能存在。不至于使我们陷入这类困难中去的可能性只有θ=60°,90°或120°。0°或180°显然也都可能。对上述结果的一种提法是:通过转动一个整圈(即完全不变动)、半圈、三分之一、四分之一或六分之一圈,图样能够保持不变。而这些就是在一个平面上所有可能的转动对称性——总共有五种。如果θ=2π/n,我们就说这是一个“n次(度)”对称性。我们说,一个n等于4或6的图样比一个n等于1或2的图样具有“较高的对称性”。
回到图30-7(a),我们看到这个图样具有四次转动对称性。在图30-7(b)中曾画出一个与图(a)具有相同对称性的另一个图样。那些像逗点模样的小图形是用来在每个方块中定义该图样对称性的一个不对称的东西。注意在相邻方块中的逗点都是彼此反转的,因而单胞比每一方块要大。假如没有那些逗点,该图样仍然会有四次对称,但单胞就会小些。图30-7的图样也还有别的对称性。例如,对任何虚线R-R的反映会再产生相同的图样来。
图30-7的图样还有另一类对称性。若该图样对Y-Y线反映并 向右(或向左)移过一个方块,则我们将得到原来的图样。这Y-Y线称为“滑移”线。
这些就是在二维中所有的可能对称性。还有一种空间对称操作,它与在二维中 的180°转动等效,但在三维中却是一个很特殊的操作,这就是反演 。所谓反演我们意指从某一原点[比方,图30-9(b)中的A点]做出的位移矢量R所指的任一点被移至-R的另一点。
图30-9的图样(a)通过反演产生出一个新的图样,但图样(b)的反演又再产生出相同的图样。对于一个二维图样来说(正如你可以从图上看出来的),通过A点对图样(b)的反演与环绕同一点做180°的转动等效。然而,假设通过想象将每一小逗点都各加上一个从页面上指出来 的“箭头”以便使图30-9(b)的图样变成个三维的图样。在经历了三维中的反演之后,所有的箭头都将倒向,因而该图样就不会 再现。若我们分别用点和叉来代表箭头和箭尾,则能造成一个如图30-9(c)所示的那种三维 图样,在反演下它是不 对称的,或者造成一个像图(d)所示的图样,那就具有 反演对称性了。注意,用转动的任何组合来模拟三维中的反演是不 可能。
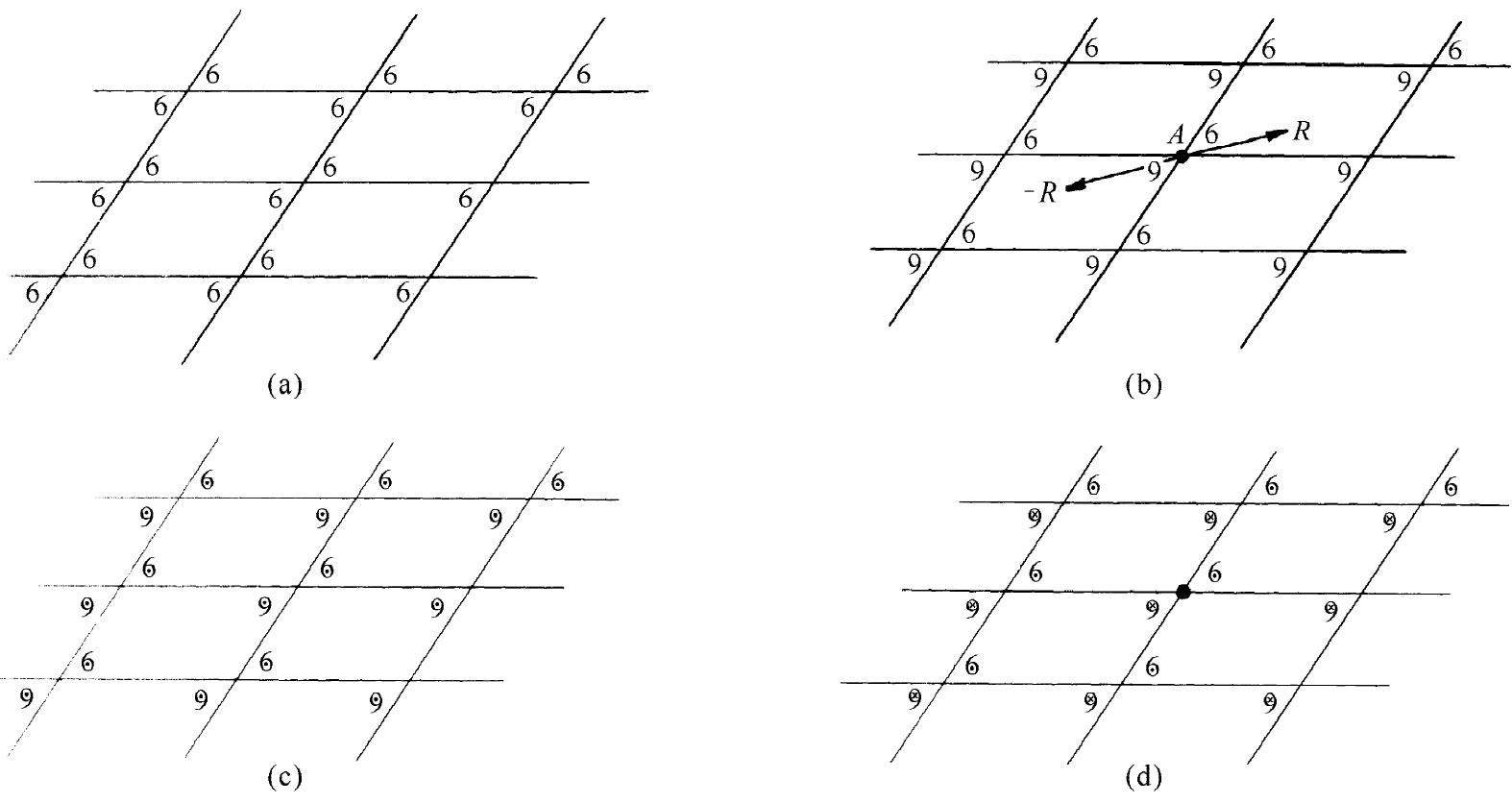
图30-9 反演对称性。若把R变成-R,图样(b)将保持不变,但图样(a)却将改变。在三维中,图样(d)具有反演对称性而图样(c)则没有
如果我们用刚才所描述的那些类型的对称操作来标志一个图样——或晶格——的“对称性”,那么结果弄清楚,对于二维可能有17种不同的图样。我们曾在图30-1中画出一个对称性可能最低的图样,而在图30-7中又画出一个对称性高的图样。把17种可能图样都画出来,作为游戏留给你们。
在这17种可能的图样中,只有寥寥几种才被用来制作墙纸和织物,那是有点奇怪的。人们始终只看到那三四种基本图样。这是因为设计者缺乏想象力,还是因为许多可能的图样都不悦目呢?