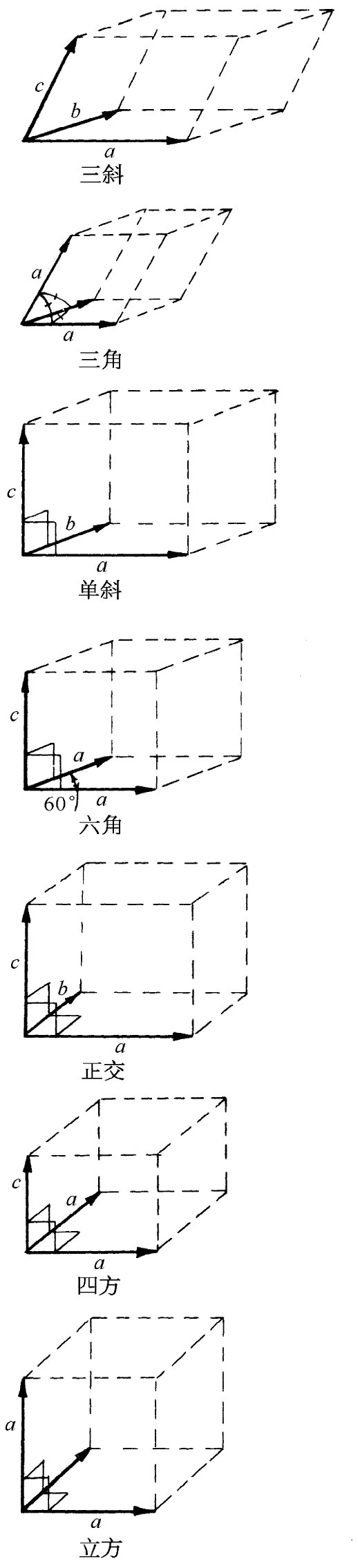
图30-10 七大类晶格
迄今我们所谈到的都只是有关二维的图样。然而,我们实际感兴趣的却是三维中的原子图样。首先,很明显的就是一块三维晶体将具备三个 基矢。于是,如果我们问起在三维中的可能的对称操作,则将发现共有230种不同的可能对称性!为了某些目的,这230种类型还可归纳成七类,它们绘在图30-10中。那对称最少的一种晶格称为三斜 类,它的单胞是平行六面体。基矢的长度各不相同,而它们间的夹角也不会有任何两个相等,所以没有任何转动或反映对称的可能。然而,仍然有两种可能的对称性——即通过对顶点的反演能使单胞改变或不改变[在三维中所谓反演我们的意思仍然是空间位移R由-R代替——换句话说,就是从(x,y,z)变成(-x,-y,-z)]。因此,三斜晶格就只有两种可能的对称性,除非在那些基矢之间存在某种特殊关系。例如,若所有的基矢长度都相等并以相同角度分隔开,则人们便有图中所示的三角 晶格。这个图形可以有一个附加的对称性,通过对体内的长对角线的转动它可以保持不变。

图30-10 七大类晶格
如果其中一个基矢,比如说c,垂直于其他两个,则我们得到一个单斜 的单胞。一个新的对称性成为可能——就是围绕着c转过180°。六角 单胞是一种其中a和b两矢量长度相等而其夹角则为60°的特殊情况,因而围绕着c所作的60°,120°或180°转动就重复相同的晶格(对于某些内禀对称性而言)。
如果所有三个基矢都互成直角,但长度不同,则将得到一个正交 单胞。这一图形在环绕那三根轴中任一根轴转过180°时都是对称的。对于其中三个基矢都互相正交而其中又有两个彼此等长的四方 单胞,则可能有较高级的对称性。最后,还有立方 单胞,那就是所有晶体之中对称性最多的了。
全部关于对称性的这种讨论其要点在于晶体的内禀对称性,有时会以巧妙的方式表现在晶体的宏观物理性质中。例如,晶体一般都有一个张量性电极化率,如果我们用极化椭球来描写该张量,则应当预期某些晶体对称性也可能会表现在该椭球中。例如,立方晶体相对于围绕三个正交方向之一的90°转动都是对称的。很明显,具有这种性质的唯一椭球就是圆球。因而立方晶体就必然是各向同性的电介质 。
另一方面,四方晶体具有四次转动对称性,所以它的椭球就必定具有两个等长的主轴,而其第三根轴必与晶轴平行。同理,由于正交晶体对三根正交轴都有二次转动对称性,所以它的这些轴就必然与极化椭球的轴相合。与此相似,单斜晶体中的一根 轴必然平行于这一椭球的三根主轴之一 ,尽管我们对其他两轴不能说些什么。由于三斜晶体不具有转动对称性,所以其椭球就可以具有完全任意的取向了。
正如你所能见到的,对算出各种可能对称性并将其与各种可能的物理张量联系起来,我们可以进行一场大的游戏。刚才仅仅考虑了极化张量,但对于其他张量——比如弹性张量——事情就会变得更加复杂。有一门称为“群论”的数学分支就是与这些课题打交道的,但通常用常识也能解决你所需要的问题。