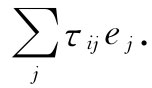
我们应当指出,从第1卷第20章后我们就已经应用过二阶张量了。在那里,我们曾用下式定义过“平面上的转矩”,诸如τxy :
τxy =xFy -yFx .
推广到三维的情况,可以写成
τij =ri Fj -rj Fi . (31.22)
τij 这个量就是一个二阶张量。为了看清楚这个张量就是这样的形式,一种办法就是通过把τij 同某个矢量相结合,比方说按照下式同单位矢量相结合,
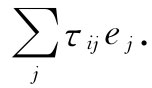
如果这个量是一矢量 ,则τij 必然会像张量那样变换,这是我们关于张量的定义。把有关τij 的式子代入,便得
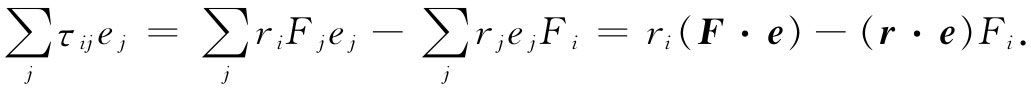
由于那些点积都是标量,所以右边两项都是矢量,因而它们之差也是矢量。因此τij 就是一个张量。
但τij 是一种特殊类型的张量,它是反对称 的,即
τij =-τji ,
所以它只有三个不等于零的项——τxy ,τyz 和τzx 。在第1卷第20章中我们已能够证明,这三项几乎是由于“偶然”才会像矢量的三个分量那样变换,以致我们可以定义 :
τ=(τx ,τy ,τz )=(τyz ,τzx ,τxy ).
我们所以说“偶然”,是因为它只发生于三维中。例如,在四维中,一个二阶的反对称张量就多达六个不等于零的项,因而肯定不能由具有四个 分量的矢量来代替它。
正如轴矢量τ=r×F实际上是一个张量那样,所以每个由两个极矢量构成的叉积也是张量——与上述相同的一切论证也都适用。可是,出自幸运,它们也可用矢量(实际上是一种膺矢)来表达,因而数学就给我们带来了方便。
从数学方面讲,若a和b是任意两个矢量,则那九个量ai bj 会形成一个张量(尽管它可能没有任何有用的物理目的)。这样,对于位置矢量r来说,ri rj 就是一个张量,而由于δij 也是一个张量,我们便明白式(31.20)的右边确是一个张量。同样,式(31.22)也是一个张量,因为其右边的两项都是张量。