
应力张量Sij 描述了物质中的内力 。如果材料是弹性的,用另一个张量Tij ——称为应变 张量——来描述其内部畸变 就较方便。对于像金属棒那样的简单物体,你知道长度的改变ΔL与作用力近似成正比,因而我们说它服从胡克定律:
ΔL=γF.
对于受了任意畸变的固态弹性体来说,应变Tij 与应力Sij 是由一组线性方程相联系的:

并且,一根弹簧(或一根棒)的势能为
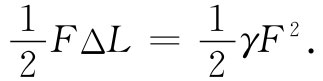
对于固体中的弹性能量密度 ,可推广为

因此晶体弹性的完整描述就必须用这些系数γijkl ,这带来了一个新的、难以控制的量,它是一个四 阶张量,由于每一个下脚标可取x,y或z中任何一个,共有34 =81个系数,但实际上却只有21个不同 数值。首先,Sij 是对称的,它只有6个不同的数值,因而在式(31.27)中就只需要36个不同 系数。可是,Sij 和Skl 可以互相交换而不改变能量,所以交换ij和kl时γijkl 必定是对称的,这样就把不同系数的数目又减少至21个。所以对于可允许的对称性最低的晶体来说,要描述它的弹性就需要21个弹性常数!当然,对于较高对称的晶体,这一数目还可以减少。例如,立方晶体只有三个弹性常数,而各向同性物质则只有两个弹性常数。
这后者的真实性可以这样理解。如同一块各向同性物质必然会对称那样,γijkl 的各分量怎么可能与坐标轴的方向无关呢?答案 是:只有 当它们可用张量δij 表达时,它们才能是与坐标无关的。有两个可能的表示式:δij δkl 和δik δjl +δil δjk ,它们都具备所需的对称性,因而δijkl 就必须是它们的线性组合。因此,对于各向同性材料来说,
γijkl =a(δij δkl )+b(δik δjl +δil δjk ),
所以这种材料就需要两个常数a和b来描述它的弹性。而立方晶体仅需要三个常数,我们将把它留给你们去证明。
作为最后一个例子,我们举出压电效应,这次是属于一个三阶张量。在应力作用下,晶体会产生一个正比于这个应力的电场,因此,一般说来,其规律是
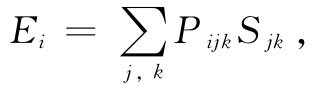
式中Ei 为电场,而Pijk 为压电系数——或压电张量。你能否证明,若晶体有一个反演中心(在x,y,z→-x,-y,-z的变换下保持不变),则所有压电系数都等于零?