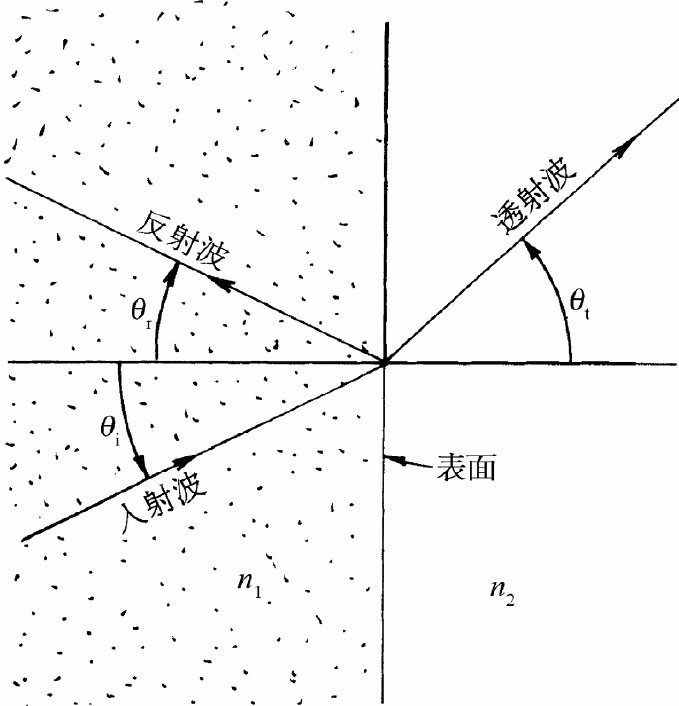
本章的主题是光(一般地说即是电磁波)在表面上的反射和折射. 我们曾在第1卷第26和33章中讨论过反射与折射定律,下面列出曾经在那里得到的一些结果:
1. 反射角等于入射角。若采用图33-1所规定的那些角,则
θr =θi . (33.1)

图33-1 在表面上光波的反射与折射(波的传播方向与各波峰垂直)
2. 对于入射和透射波束,乘积nsinθ彼此相等(斯涅耳定律):
n1 sinθi =n2 sinθt . (33.2)
3. 反射光的强度取决于入射角和偏振方向。对于E与入射面正交的情况,反射系数R⊥ 为
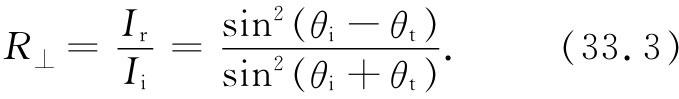
对于E与入射面平行的情况,反射系数R‖ 为
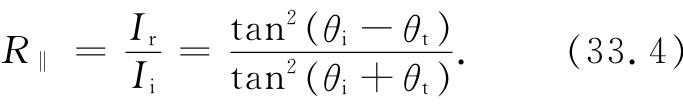
4. 对于法向入射(当然,不论哪一种偏振!),

以前,我们曾用i代表入射角,r代表折射角。由于不能对“折射”角和 “反射”角两者都用r,所以现在就采用θi =入射角,θr =反射角,而θt =透射角。
我们以前所讨论的内容实际上是任何人至今正常跟上这个课题所需要的,但我们现在要用一种不同的方法完全重做一遍。为什么?一个原因是,以前我们假定折射率是实数(在材料中没有吸收)。另一个原因是,你应该知道怎样从麦克斯韦方程组的观点去处理波在表面上发生的情况。我们将得到与以前相同的答案,但目前却是从波动问题的一个直接解,而不是从某些聪明的论证得到的。
我们要强调,表面反射的振幅并不像折射率那样是材料 的属性。它是一个“表面特性”,严格地取决于该表面是怎样构成的。在折射率为n1 和n2 的两种材料之间表面上一薄层额外的杂质往往会改变反射的情况(这里有各种类型干涉的可能性——像油膜的五颜六色。对某给定的频率适当的厚度甚至可以使反射波的振幅降低至零,那就是镀膜透镜的制作原理)。我们将要导出的公式,只在折射率的改变很急速——发生在一个与波长相比很小的距离之内——时才正确。对于光来说,其波长约为5000Å,从而所谓“光滑”面我们指的是这样一种面:在面内经过仅仅几个原子(或几个Å)的距离,状况就改变。我们的方程式对于光在高度磨光的表面上将是有效的。一般说来,如果折射率是在超过几个波长的距离上逐渐改变的,则根本就很少反射。