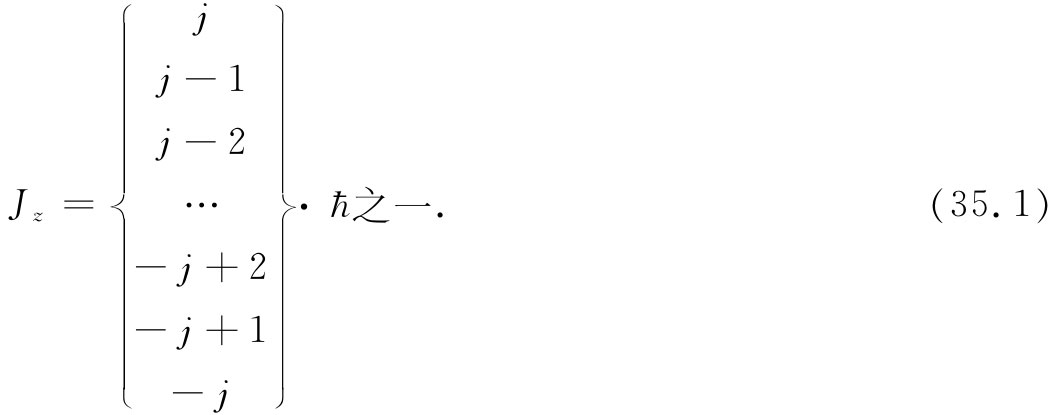
上一章我们曾描述过在量子力学中一物体的角动量怎么会不具有任意方向,而在一给定轴上它的分量却只能取某些间隔相等的分立值,那是一件令人震惊而又独特的事情。你可能认为,在你的智力达到更高水平并准备好接受这种概念之前也许不应该探索这种事情。实际上,就能够轻易地接受这样一件事情的意义上来说,你的智力将永远不会变得更高级。并没有任一种描述方法可以使其明白易懂,而同时在其本身的形式上又不会那么微妙和高级以致比起你企图要加以解释的东西更复杂。在小尺度范围内的物质行为——正如我们曾经多次提到的——与通常所熟悉的任何事情都不相同,而且确实十分奇怪。当我们继续讲解经典物理时,试图对小尺度范围内物质的行为得到一个逐渐增长的感性认识,开始的时候作为一种缺乏任何深刻理解的经验,乃是一个好主意。对这些事情的理解,在任何程度上都是很慢地达到的。当然,人们逐步变成能够更好地懂得在量子力学情况下所发生的事情——如果这就是所谓理解的涵义——那么人们将永远得不到一个认为量子力学法则是“自然的”那种舒舒服服的感觉。当然那些法则的确 是“自然的”,但对于我们本身在普通水平的经验上来说它们却不是自然的。我们对待这一角动量的法则的态度与过去对待许多曾经谈到的其他东西的态度很不相同,这一点应该有所解释。我们并不试图解释“它”,但至少必须告诉 你们发生的情况,要对材料磁性进行解释而又不提及有关磁性——包括角动量和磁矩——的那种经典解释乃是不正确的,那可能是不诚实的。
关于量子力学的一个最令人震惊而又扰乱人心的特征在于:如果你沿任一根特定轴取角动量,则你会发现它总等于一整数或半整数乘以ћ。不管你取的是哪一根轴,结果是一样的这一奇怪事实——你可取任一根其他轴并发现在它上面的分量也被固定在那同一组数值上——所涉及的微妙之处我们将留在后面一章中讨论,到那时你将会因看到这一表观佯谬如何最后获得解决而感受到欢欣鼓舞。
目前我们将仅仅接受这个事实,即对于每个原子系统就有一个数值j,称为该系统的自旋 ,它必须是一个整数或一个半整数,而沿任一特定轴的角动量分量则将始终具有下列从+jћ到-jћ之间的那些值之一:
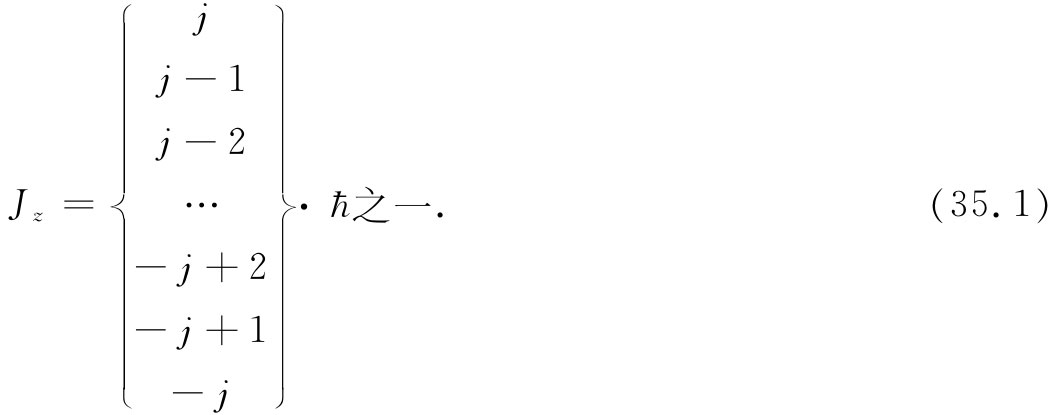
我们也曾提及每个简单原子系统都有一个与角动量的方向相同的磁矩。这不仅对于原子和核正确,而且对于基本粒子也都正确。每个基本粒子有其本身的特征值j和磁矩(对于某些粒子来说,这两者均为零)。在这一句话中,所谓磁矩我们指的是,比方说在一个沿z方向的磁场中,对于小磁场来说系统的能量可以写成-μz B。我们一定要有磁场不应太大的条件,否则它就可能会干扰该系统的内部运动,从而能量不会成为磁场发动前存在的那个磁矩的一种量度。但如果场足够弱,则由该场所改变的能量由量
ΔU=-μz B (35.2)
表示,而条件是在这个式子里的μz 要由下式来代替:
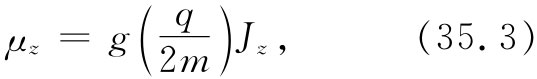
其中Jz 就是式(35.1)中那些数值之一。
假设考虑一个自旋为j=3/2的系统。在没有磁场时,该系统就有四个不同的可能状态,这些状态对应于那些不同的Jz值,但都具有完全相同的能量。可是一旦我们加上磁场,就有一个附加的相互作用能量把这些状态分隔开,形成四个稍微不同的能级。这些能级的能量是由某些与B成正比而又乘以Jz 值(3/2、1/2、-1/2和-3/2)的ћ倍给出。关于自旋分别为1/2、1和3/2的原子系统的能级分裂,如图35-1的那些简图所示(记住对于电子的任何配置,磁矩始终与角动量反向)。
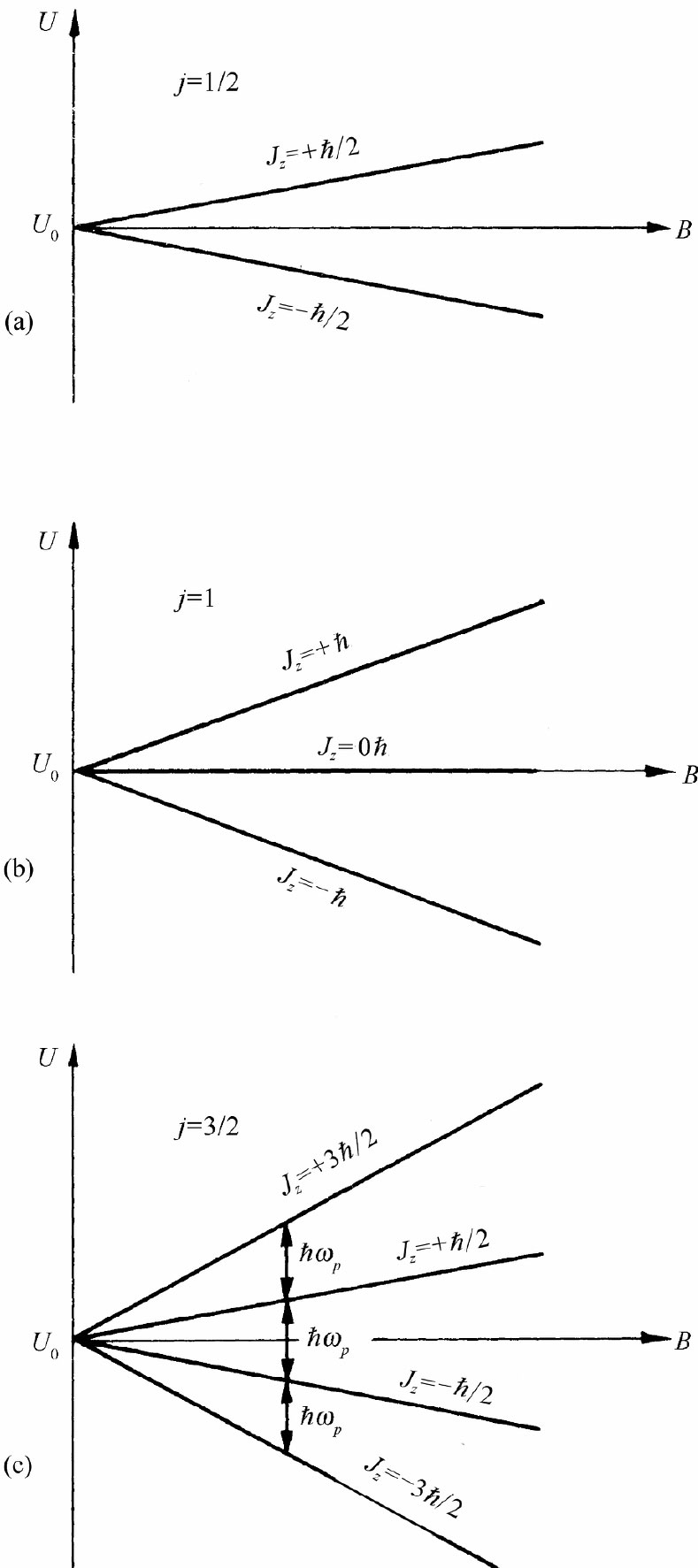
图35-1 自旋为j的一个原子系统在磁场B中具有(2j+1)个可能能量,对于小场来说,能量间隔与B成正比
你将从图上注意到,那些能级的“重心”在有磁场和没有磁场时都一样。并且注意到,对于给定磁场中的某个给定粒子来说从一个能级至下一能级的间隔总是相等的。对于某一给定磁场B我们想把能量间隔写成ћωp ——这仅仅是ωp 的定义。利用式(35.2)和(35.3),我们得
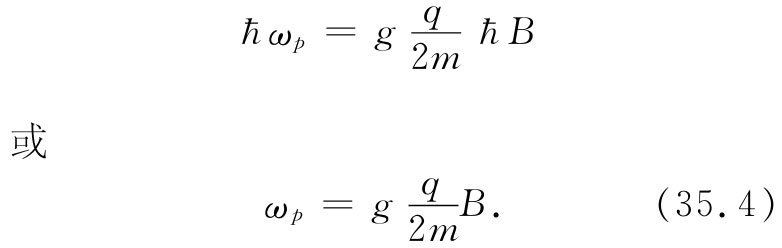
量g[q/(2m)]恰好就是磁矩对角动量的比——它是该粒子的一种性质。式(35.4)与我们在第34章中得到的角动量为J而磁矩为μ的陀螺仪在磁场中的进动角速度的公式相同。