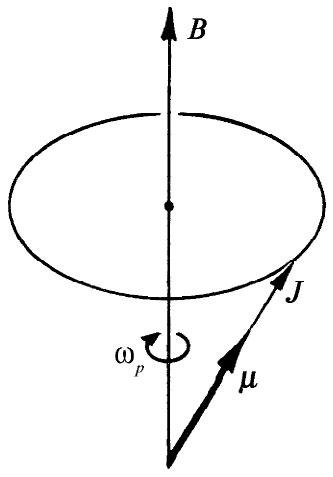
图35-3 具有磁矩μ和角动量J的原子的经典进动
现在我们要来描述一种由拉比及其同事们所发展起来的、经改进的测量磁矩用的仪器。由于在斯特恩格拉赫实验中原子的偏移很小,因而磁矩的量度并不是很精确。拉比的技术使得磁矩的测量有可能达到难以想象的精度。这一方法是以这种事实为基础的,即原子的固有能量在磁场中被分裂成有限数目的能级。一个原子在磁场中的能量只能有某些分立值,这件事实际上并不比原子一般 只具有某些分立能级的事实——我们在第1卷中曾经常提及的某些事情——更令人诧异。为什么这同样的事情对处于磁场中的原子来说就不成立呢?它仍然成立。但正是希望把这一事实与取向磁矩 的概念相联系的意图才给量子力学带来某些奇怪的含意。
当一原子具有能量差约为ΔU的两个能级时,它可以通过发射一个频率为ω的光量子,从较高的能级跃迁到较低的能级。ω满足下式
ћω=ΔU. (35.7)
处于磁场中的原子也可以发生同样的事情。只是此时,能量差竟会那么小以致该频率与光对应不起来,而是对应于微波或无线电波。原子从低能级至较高能级的跃迁,也可通过对光的吸收而发生,对于原子处于磁场中的情况则通过对微波能量的吸收而实现。这样,如果有一个原子处于磁场中,则我们可以通过加一频率适当的附加电磁场使其从一个态跃迁至另一个态。换句话说,若有一个处在强磁场中的原子,而我们用一个弱的变化电磁场来“扰动”该原子,则会存在某个概率把它撞到另一个能级上去,只要该频率接近于式(35.7)中的ω值。对于一个处在磁场中的原子,这个频率恰好就是我们以前曾称之为ωp 的、根据式(35.4)用磁场所给出的那个频率。若该原子受一错误频率扰动,则能够引起跃迁的机会将十分微小。于是在引起跃迁的概率内就有一个在ωp 处的尖锐共振 。通过在一已知磁场B中测量这个共振频率,我们就能以巨大的精度测得量g[q/(2m)]——从而也测得了g因子。
十分有趣,人们从经典的观点也会得出相同的结论。按照经典图像,当我们把一个磁矩为μ而角动量为J的小陀螺仪置于一外磁场中时,该陀螺仪将环绕平行于磁场的轴进动(见图35-3)。假设我们要问:如何改变经典陀螺仪相对于场——也即相对于z轴——的角度呢?磁场会产生一个绕水平 轴的转矩。你会认为这样的转矩正在试图 使该磁体与场排成直线,可是它却仅仅引起了进动。如果想要改变该陀螺仪相对于z轴的角度,那就必须对它施一环绕z轴 的转矩。倘若所施的是一个与进动同向的转矩,则该陀螺仪的角度将会这样改变以给出一个在z方向较小的J分量。在图35-3中,J与z轴间的夹角将会增大。若试图阻止进动,J会朝着垂直方向运动。

图35-3 具有磁矩μ和角动量J的原子的经典进动
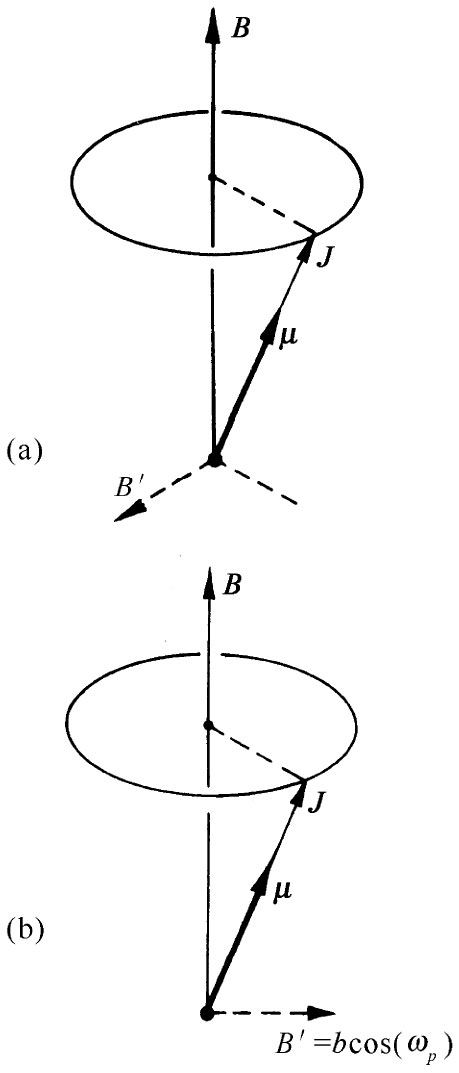
图35-4 一个原子磁体的进动角度,可以通过始终垂直于μ的、如在(a)或(b)中的一个振动着的水平磁场来加以改变
对一个在均匀场中正在进动的原子,如何才能加上我们所要的那种类型的转矩呢?答案是,从旁加一个弱磁场。乍看起来你也许认为这个磁场的方向必须随同磁矩的进动一起旋转,使得它总是垂直于磁矩,如图35-4(a)中由场B′所指出的那样。像这样的场会工作得很好,但一个交变 的水平场几乎同样优良。如果有一个小的水平场B′,它总是在(正的或负的)x方向上而且以频率ωp 振动着,那么在每个半周期内施于磁矩上的力矩就将倒转方向,以致它具有一个积累效应,该效应几乎与一转动的磁场同样有效。于是,从经典方面说,我们就会期待,若有一个频率恰恰为ωp 振动着的很弱的磁场,则磁矩沿z方向的分量就应该改变。当然,按照经典理论,μz 应该是连续变化的,但在量子力学中这磁矩的z分量就不能做连续调整,它必须从一个值突然跳跃至另一个值。我们已做出了经典力学与量子力学两种结果之间的比较,为你们提供在经典理论中也许会发生的某种事情与在量子力学中实际发生的事情如何联系起来的线索。顺便说说,你将会注意到,该期待的共振频率在这两种情况下是相同的。
又一附注:从我们所曾谈到的关于量子力学的事情来看,并没有明显的理由说明为什么不能够在2ωp 的频率也发生跃迁。碰巧在经典情况下没有任何与此类似的东西,而在量子力学中也不会发生这种跃迁——至少对于我们刚才所述的那种独特诱导跃迁的方法来说是不会发生的。采用一个水平方向的振动磁场,频率2ωp 引起同时跳跃两步的概率等于零。只有在频率ωp ,无论向上或向下的跃迁才可能发生。
现在,我们准备来描述有关测量磁矩的拉比方法。这里将仅仅考虑对自旋为1/2的那种原子的操作。仪器设备的简图如图35-5所示。有一个熔炉,它发出的中性原子流直通过直线排列的三组磁铁。磁铁1几乎与图35-2中的一样,具有强大的场梯度——比方说,其∂Bz /∂z为正。如果原子有一磁矩,而且Jz =+ћ/2,则它会被向下偏转;如果Jz =-ћ/2,则将被向上偏转(因为对于电子来说,μ的方向与J的方向相反)。若只考虑那些能穿过狭缝S1 的原子,就有如图所示的两条可能轨道。凡Jz =+ћ/2的原子必定沿曲线a穿过该狭缝,而凡Jz =-ћ/2的原子则必定沿曲线b通过。从熔炉发出来的、沿其他路径的原子将不会穿过该狭缝。
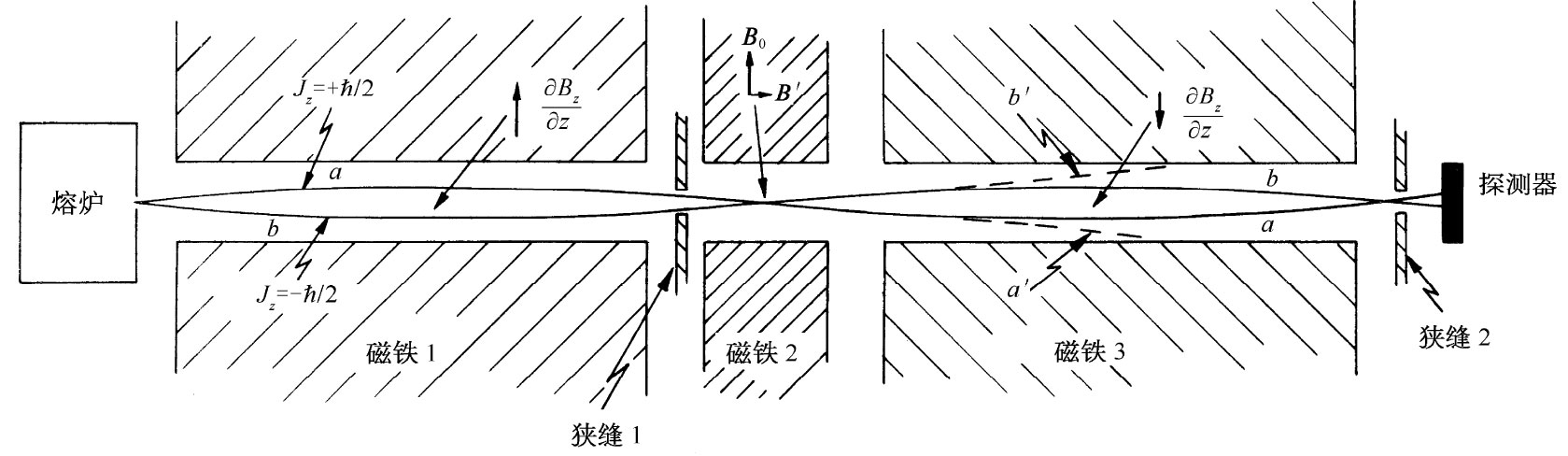
图35-5 拉比的分子束仪器
磁铁2产生一个匀强场。在这一区域中没有力施于原子上,因而它们将直接通过而进入磁铁3中。磁铁3恰好像磁铁1,但其场是反转过来 的,所以∂Bz /∂z具有相反符号。那些具有Jz =+ћ/2(我们讲“自旋向上”)的原子,先前在磁铁1中被推向下的,现在在磁铁3中却被推向 上了,它们将继续沿着路径a穿过狭缝S2 到达探测器。那些具有Jz =-ћ/2(即“自旋向下”)的原子,在磁铁1和磁铁3中也各受到反向的力而沿路径b穿过狭缝S2 达到探测器。
探测器可以用各种不同方式制成,这取决于被测量的原子。例如,对于像钠一类的碱金属原子,探测器可以是一根与一灵敏电流计相连接的细热钨丝。当钠原子到达钨丝上时,Na+ 离子被蒸发出去,留下来一个电子。因此在该导线上就有一个正比于每秒到达的原子数目的电流。
在磁铁2的间隙中有一组能产生小的水平磁场B′的线圈。这组线圈由以一可变频率ω振动的电流所驱动,所以在磁铁2的两极间就有一个强大而恒定的垂直方向的磁场B0 和一个弱小的振动着的水平磁场B′。
现在假设该振动场的频率ω被调至ωp 处——即处于场B中原子的“进动”频率。这交变场将使某些从旁经过的原子作出从一个Jz 值至另一个Jz 值的跃迁。一个原来自旋“向上”(Jz =+ћ/2)的原子可能给翻转“向下”(Jz =-ћ/2)。此时这个原子已把它的磁矩方向倒转了,因而它将在磁铁3中感受到一个向下 的力并将沿着路径a′运动,如图35-5所示。它将不再穿过狭缝S2 而到达探测器了。同理,有些原子原来自旋是向下(Jz =-ћ/2)的,当经过磁铁2时将被翻转向上(Jz =+ћ/2),于是它们将沿着路径b′而不会到达探测器。
若振动场B′的频率与ωp 明显不同,则它将不会引起任何自旋的倒转,因而各原子将按照它们不受干扰的路径到达探测器。因此你可以看到,原子在B0 场中的“进动”频率ωp 可以这样求得,即变更场B′的频率ω直到抵达探测器的原子流的减弱被观测出来。原子流的下降将发生在ω等于ωp 的“共振”时刻。探测器中的电流作为ω的函数曲线或许看来像图35-6所示的那样。知道了ωp ,就能得到原子的g值。
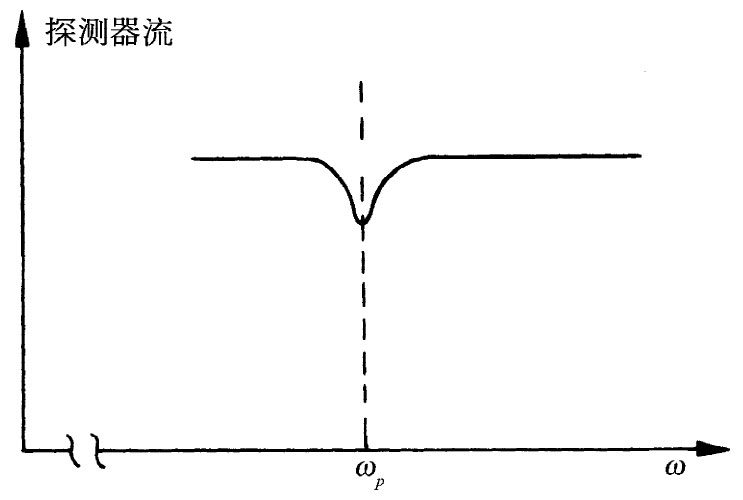
图35-6 当ω=ωp 时,在束中的原子流就会减弱
像这样的原子束、或通常被称为“分子”束的共振实验,是测量原子客体磁性的一种漂亮而又精密的方法。这共振频率ωp 可以用极高的精度测得——事实上,比起我们对(为了求g而必须知道的)磁场B0 可能进行的测量要精确得多。