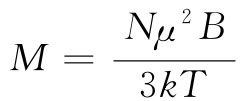（35.9）现在我们很想描述大块材料的顺磁现象。假设有一种物质其原子具有永磁矩，比如像硫酸铜那样的晶体。在这种晶体中存在这样的铜离子，其内部的电子壳层有一净角动量和一净磁矩。所以这种铜离子就是一个具有永磁矩的物体。请让我们就这件事说一句，有些原子具有磁矩而有些不具有。任何比如像钠那种含有奇数 个电子的原子，将具有磁矩。钠有一个电子位于它的未填满的壳层内，这个电子给该原子一个自旋和一个磁矩。然而，通常当化合物形成时，在外壳层中的额外电子就会与自旋方向恰巧相反的其他电子互相耦合，使得所有价电子的角动量和磁矩都经常被抵消掉，这就是为什么分子一般都不具有磁矩的原因。当然，如果是钠原子气体，则不会有这样的抵消作用 [1] 。并且，如果你有那种在化学中所谓“自由基”的东西——一种具有奇数个价电子的物体——则键不会完全被满足，因而就有一个净角动量。
在多数大块材料中，只要存在其内 电子壳层未被填满的原子就具有净磁矩，此时可能会有一个净角动量和磁矩。这样的原子在周期表中的“过渡元素”部分被找到了——诸如铬、锰、铁、镍、钴、钯和铂等就是这一类元素。此外，所有的稀土元素也都具有未填满的内壳层和永久磁矩。还有其他两三种奇怪的东西会偶而具有磁矩，诸如液态氧，但我们将把它留给化学系去解释原因。
现在，假设有一个箱子充满了具有永久磁矩的原子或分子，比如气体、液体或晶体。我们想要知道，当加上一外磁场时将会发生什么情况。当没有 磁场时，原子因热运动而被到处撞来撞去，因而它们的矩在所有方向上转来转去。一旦有了磁场时，它就使那些小磁体整齐排列起来，于是趋向场的矩比离开场的矩就多些，即该材料已被“磁化”了。
我们将把材料的磁化强度 M定义为单位体积中的净磁矩，而这指的是单位体积内原子磁矩的矢量和。如果单位体积中有N个原子，而它们的平均 磁矩为〈μ〉平均 ，则M可以写成N乘以平均原子磁矩：
M=N〈μ〉平均 . （35.8）
M的定义相当于第10章中关于电极化强度P的定义。
顺磁性的经典理论很像第11章中曾向你们表明的有关介电常量的理论。人们假定每个原子都有一个磁矩μ，它的大小固定，但其方向是任意的。在场B中，其磁能为-μ·B=-μBcosθ，其中θ为矩与场之间的夹角。根据统计力学，具有任意角度的相对概率为e-能量/（kT） ，因而靠近零度的角比靠近π的角更可能出现。同以前在§11-3中所进行的步骤完全一样，我们会发现，对于小磁场来说，M平行于B，大小为
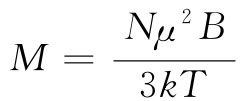（35.9）
［见式（11.20）］。这一近似公式只对μB/（kT）比1小得多时才正确。
我们已求得感生磁化强度——单位体积中的磁矩——与磁场成正比，这即是顺磁性现象。你将会看到，这效应在低温时较强而在高温时较弱。当我们在该物质上加一磁场时，对于弱场会产生一个正比于该场的磁矩。M对B的比率（对于弱场而言）称为磁化率 。
现在，我们要从量子力学观点来考察顺磁性。首先考虑原子自旋为1/2的情况。在没有磁场的情况下，原子具有某个能量；但当处于磁场中时，就有两个可能的能量，每一个Jz 值对应一个能量。对于Jz =+ћ/2，能量被磁场改变的量为
（由于电子的电荷为负 [2] ，因此对于一个原子来说能量移动ΔU1 是正的）。对于Jz =-ћ/2，能量被改变的量为
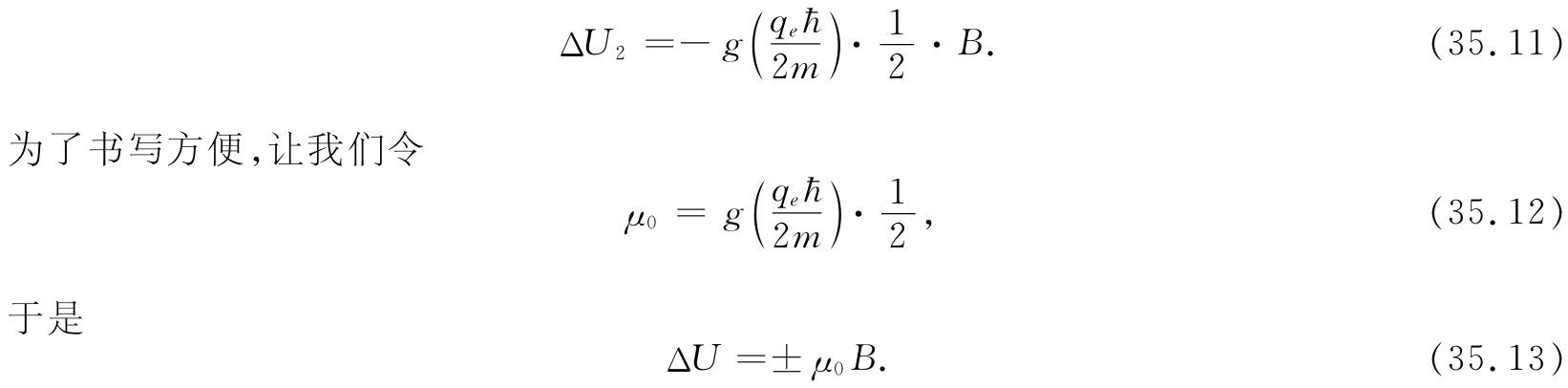
μ0 的意义很明显：-μ0 是在自旋向上的情况下磁矩的z分量，而+μ0 则是在自旋向下时磁矩的z分量。
可是统计力学告诉过我们，一个原子处在一个态或另一个态，其概率正比于
e-（态的能量）/kT .
当没有磁场时，这两个态具有相同能量，所以当在磁场中达到了平衡时，概率就正比于
e-ΔU/kT . （35.14）
单位体积中自旋向上的原子数为
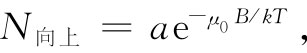（35.15）
而自旋向下的原子数为
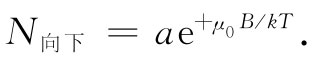（35.16）
常数a是被这样确定下来的，即
N向上 +N向下 =N， （35.17）
式中N为单位体积中的原子总数。因此就得到
我们所感兴趣的是沿z轴的平均 磁矩。由于自旋向上的那些原子将各贡献-μ0 之矩，而自旋向下的那些原子则各贡献+μ0 之矩，因而平均矩为
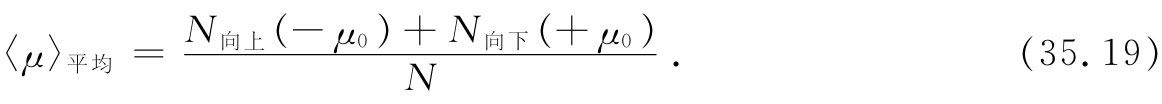
于是单位体积中的磁矩M就是N〈μ〉平均 。利用式（35.15）、（35.16）和（35.17），便可得到
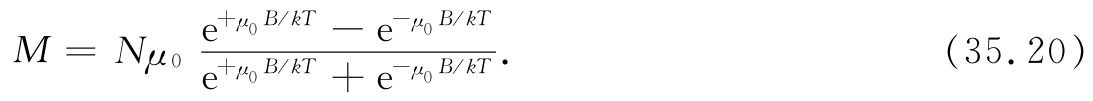
这就是关于j=1/2的原子其M的量子力学公式。顺便提及，这个式也可以用双曲正切函数写得更简洁些：
M作为B的函数其曲线如图35-7所示。当B变得非常大时，双曲正切函数趋于1，因而M趋于其极限值Nμ0 。所以在强场的情况下，磁化达到饱和 。我们可以明白为什么会这样，在足够强的场中，磁矩全部被排列在同一个方向上了。换句话说，它们全都处于自旋向下的状态，因而每一原子贡献一个磁矩μ0 。
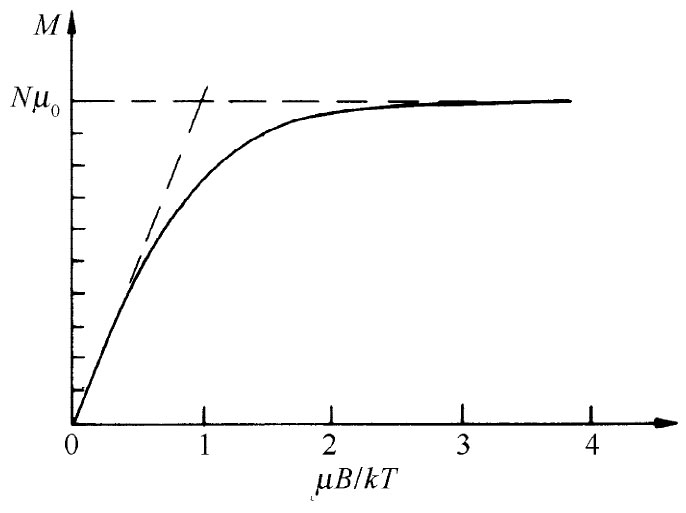
图35-7 顺磁性磁化强度随磁场强度B的变化
在大多数正常情况下——比如说，对于典型的矩、室温以及我们通常能够获得的场强（诸如10000Gs）——比值μ0 B/kT约等于0.002。人们一定要达到极低温度时才能见到饱和现象。对于常温来说，我们往往能够用x来代替tanhx，因而上式可以写成
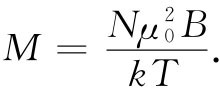（35.22）
正如我们曾在经典理论中见到的，M与B成正比。事实上，这个式子几乎和以前的完全相同，除了因子1/3似乎不见了以外。但我们仍需要把量子力学中的μ0 同式（35.9）经典结果中出现的μ联系起来。
在经典公式中，出现的是μ2 =μ·μ，即矢量磁矩的平方，也即
我们曾在上一章中指出，通过用j（j+1）ћ2 代替J·J，你就很可能会从经典的计算结果中得到正确答案。在我们这个特殊例子中，j=1/2，因而
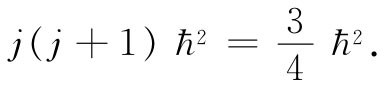
若用此来顶替式（35.23）中的J·J，则可得
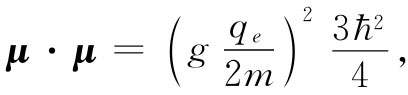
或者利用式（35.12）所定义的μ0 ，我们得
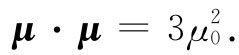
用这个结果代替经典公式（35.9）中的μ2 ，的确会重现正确的量子公式（35.22）。
关于顺磁性的量子理论很容易推广到任意自旋j的原子。弱场磁化强度为
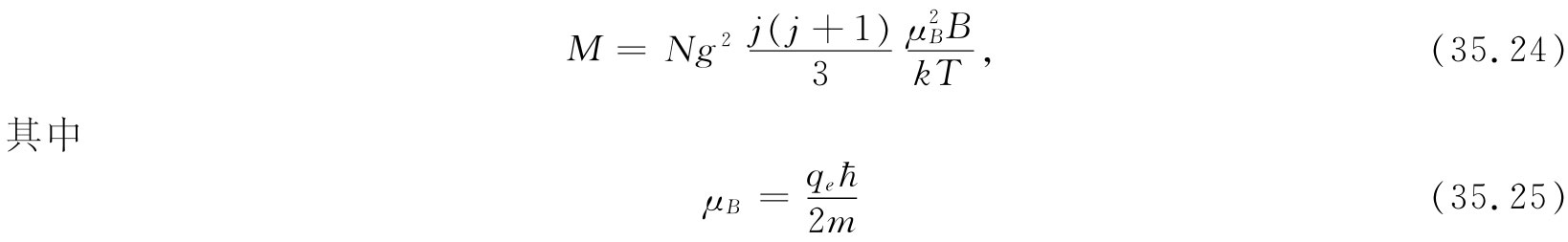
是一个具有磁矩量纲的常数组合。大多数原子都具有近似这种大小的磁矩。它被称为玻尔磁子 。电子的自旋磁矩就几乎正好是一个玻尔磁子。