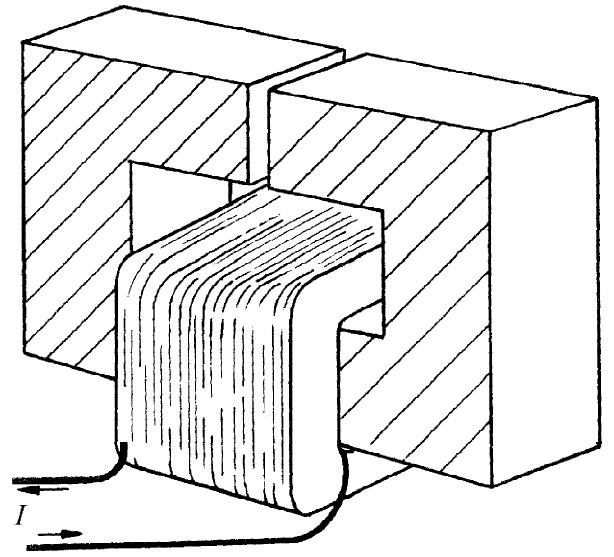
图36-10 电磁铁
现在让我们来讨论一种稍微复杂些的实际情况。假设有一块如图36-10所示的、形式相当标准的电磁铁——由一块“C形”轭铁以及绕在这块轭铁上的多匝导线圈制成。缝隙中的磁场B将会怎样呢?

图36-10 电磁铁
如果缝隙厚度比所有其他尺寸都小,则作为一级近似,可以认为B线将环绕整个回路,正如它们在铁环中所表现的那样。它们看来有点像图36-11(a),在缝隙处往往散开一些,但若缝隙很窄,则这种散开只是一个微小的效应。假设通过轭铁任一截面的B通量是一个常数,这是一个相当好的近似。如果轭铁具有均匀的横截面积——而我们又忽略在缝隙处和在转弯处的任何边界效应——那么便可以讲,环绕轭铁的B是均匀的。
并且,在缝隙中B将有同样的数值,这是从式(36.16)得出来的结论。试想象如图36-11(b)所示的闭合曲面S,它的一个面位于缝隙中而另一个面位于铁中,从这个闭合曲面跑出来的总B通量必为零。如果把缝隙中的场称为B1 ,而把铁里的场称为B2 ,则我们得
B1 A1 -B2 A2 =0.
由于A1 =A2 (在我们的近似程度下),所以可推断B1 =B2 。
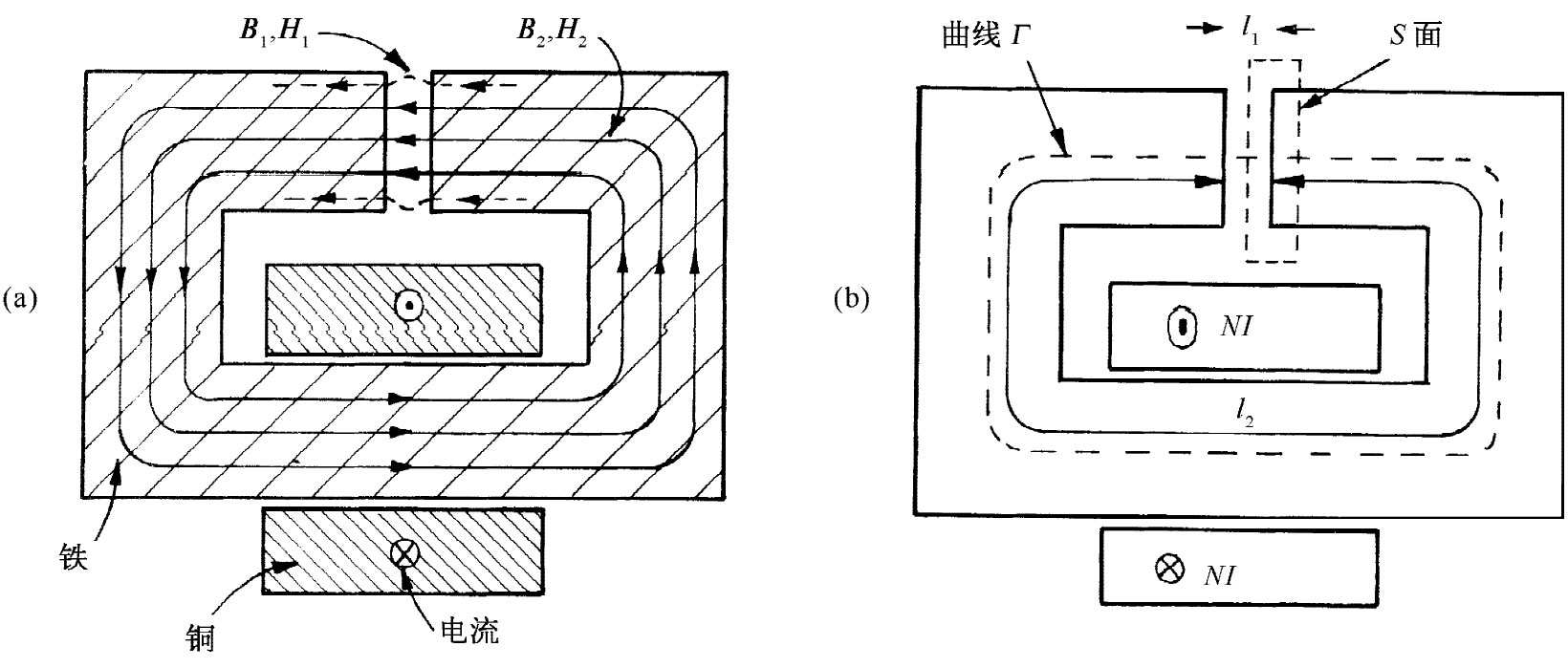
图36-11 电磁铁的截面
现在让我们来看看H。可以仍然利用式(36.19),环绕图36-11(b)中的曲线Γ进行线积分。右边的积分照旧是NI,即匝数乘电流。然而,现在铁里和空气中的H将不相同。称铁里的场为H2 ,环绕轭铁的路径长度称为l2 ,则这一部分的曲线将对该积分贡献量H2 l2 ;把缝隙里的场称为H1 ,假定缝隙厚度为l1 ,则可获得来自缝隙的贡献H1 l1 。于是我们有
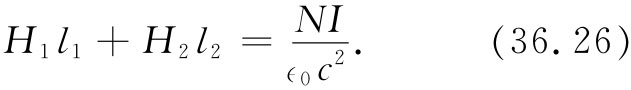
现在还知道另外一些情况:由于在空气缝隙里磁化强度可以忽略,因而B1 =H1 。由于B1 =B2 ,所以式(36.26)变成
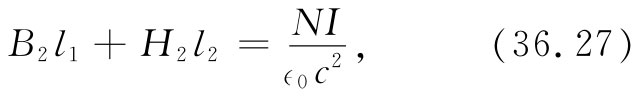
我们仍然有两个未知数。为了求得B2 和H2 ,还需要另一个关系式——即把铁中的B,H联系起来的关系式。
如果可作B2 =μH2 这个近似,则就能用代数法求解上述方程。然而,让我们考虑普遍的情况,即其中铁的磁化曲线如图36-8所示。我们希望得到的就是这个函数关系与式(36.27)结合后的联立解。这个解可以这样找到,通过把式(36.27)的曲线和磁化曲线画在同一个图上,如图36-12所示,两条曲线相交之处,就是我们要求的解。
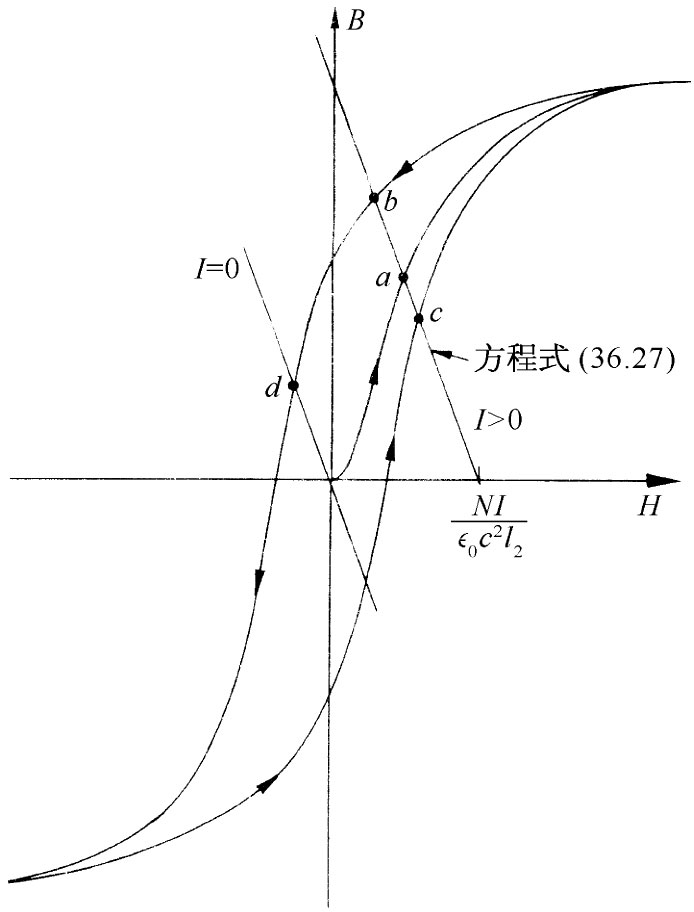
图36-12 求解电磁铁中的场
对于一给定电流I,函数式(36.27)就是图36-12中标明I>0的直线。该线与H轴(B2 =0)相交于H2 =NI/(∈0 c2 l2 )处,而其斜率为-l2 /l1 。不同的电流仅仅是沿水平方向移动该直线。从图36-12我们看到,对于一给定电流可以有几个不同的解,这取决于你怎样到达那里。如果你刚好制成该块磁铁,并接通电流而上升到了I,则场B2 (也即B1 场)的值就将有点a给出。如果你已经使电流达到某个很大的值,而下降至I,则场将由点b给出。或者,如果在磁铁中你刚好有一个高负值电流,然后才把它升高 至I,则场就是c点处的场。因此,缝隙里的场将取决于你在过去做过的事情。
当磁铁中的电流为零时,式(36.27)中B2 和H2 的关系式用图中标明为I=0的那条直线来表示。仍然存在各种可能的解。如果你先使铁达到了饱和,则可能存在一个由d点给出的、在磁铁里相当大的剩余磁场。你可以将线圈除掉,从而得到一个永久磁体。由此可见,若要制成一块优质永久磁体,你必须要有宽 磁滞回线的材料。诸如铝镍钴V族那类特种合金,就具有很宽阔的磁滞回线。