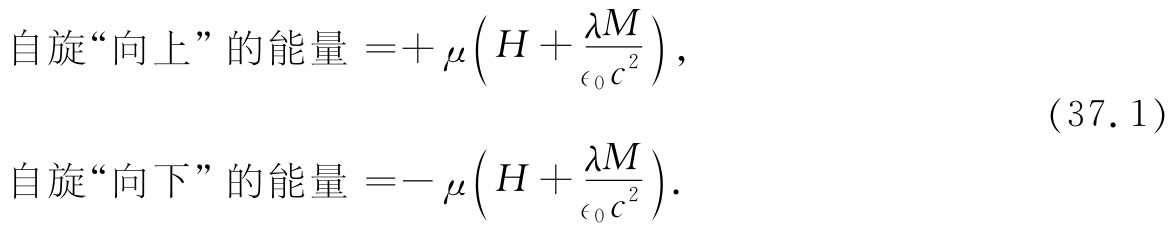
在本章中,我们将讨论铁磁性材料和其他一些奇异磁性材料的行为和特点。然而,在对磁性材料进行研究以前,我们将十分迅速地复习一下上一章中学过的某些有关磁铁方面的普遍理论。
首先,想象材料内部引起磁性的原子电流,然后再用体电流密度j磁化 =▽×M来描述它。我们要强调,这并不认为它代表那些实际 电流。当磁化强度均匀时,电流也并非真 的恰好互相抵消。也就是说,在某原子中一个电子的旋转电流与在另一个原子中一个电子的旋转电流并不会以这样的方式交叠,以致其总和恰好等于零。即使在单个原子内部,磁性的分布也不是 平滑的。例如,在铁原子中,磁化强度被分布在一个近似是球形的壳层上,它既不很靠近核,也不离核太远。因而,物质中的磁性就其细节而言是很复杂的事情,它非常不规则。然而,我们现在不得不略去这种细致的复杂性,而从整体的、平均的观点来讨论那些现象。于是在任何比原子大的有限范围内,当M=0时,在内部区域里的平均 电流确实为零。因此,在目前我们正在考虑的程度,所谓单位体积的磁化强度以及j磁化 等等,我们指的都是在比单个原子所占空间要大的区域里的平均。
在上一章中,我们也曾发现铁磁材料具有如下的重要性质:在超过某一温度时,它并不具有强磁性,而在这一温度之下才会变得有磁性。这个事实不难被演示出来。一段镍线在室温时会被一块磁铁吸引。然而,如果用煤气火焰把它加热至高于其居里点时,则它便变成非磁性体,此时即使被带至磁铁近旁,也不会为磁铁所吸引。如果让它在磁铁近旁冷却,则当温度降至临界温度以下时便会突然再度被磁铁吸引!
我们将采用的有关铁磁性的普遍理论,假定电子的自旋导致了磁性。电子的自旋为1/2并带有一个玻尔磁子的磁矩μ=μB =qe ћ/(2m)。电子自旋可“向上”也可“向下”。由于电子有负电荷,所以当其自旋“向上”时,就有一个负 的矩,而当其自旋“向下”时则有一个正 的矩。按照我们常用的惯例,电子的磁矩μ与其自旋反向。我们已求得一个磁偶极子在给定外加磁场B中的取向能为-μ·B,可是一个自旋电子的能量也取决于邻近自旋的排列情况。在铁中,若附近一原子的磁矩“向上”,则与之相邻的另一原子就有使其本身磁矩也同样“向上”的强烈倾向。这就是促使铁、钴、镍等具有如此强大磁性的因素——磁矩全都必须互相平行。我们不得不讨论的第一个问题就是这个为什么 。
量子力学发展起来之后不久,人们就注意到存在一个很强的表观力 ——既不是一种磁力,也不是任何其他种类的真实力,而只是一种表观力——试图把相邻电子的自旋互相反向 整齐排列。这些力与化学键力密切相关。在量子力学中有一个原理——称为不相容原理 ——两个电子不能处于完全相同的状态,即它们的位置和自旋取向不能完全相同。例如,若它们位于相同的地点,则唯一可能的就是它们的自旋相反。因此,如果两原子之间有一个空间区域,电子乐于聚集在那里(像在化学键中那样),而我们也想把另一个电子放在已经呆在那里的一个电子的上面,则唯一办法就是将这第二个电子的自旋指向与第一个电子的自旋指向相反。要使它们的自旋平行是违反规律的,除非这两个电子间互相离得很远。这样就产生了一个效应,即一对互相靠近、自旋平行的电子比一对自旋相反的电子具有大得多的能量。净效应好像有一个企图把自旋翻转过来的力,有时把这种使自旋翻转的力称为交换力 ,但那样只能使它更加神秘——并不是一个很好的名称。只是由于不相容原理才使得电子具有一种促使其自旋相反的倾向。事实上,这就是关于几乎一切物质都缺乏 磁性的解释!原子外部自由电子的自旋具有在相反方向达到平衡的强大趋势。问题是要来解释为什么像铁那样的材料其性质恰恰与我们所预期的相反。
对想象的排列效应我们已在能量公式中加上一个适当的项而加以概括了,即假定如果邻近的电子磁体具有平均磁化强度M,则电子的磁矩就具有同邻近原子的平均磁化强度处于相同方向的强大趋势。这样,就可以将两种可能的自旋取向写成 [1] :
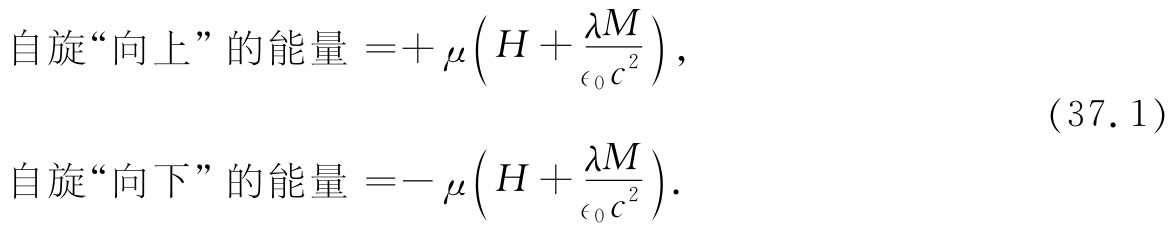
当弄清楚量子力学可能会提供一个巨大的自旋取向力时——即使其符号显然错误——人们曾认为铁磁性也许都起源于这同一种力。由于铁的复杂性以及牵涉到大量电子,所以这互作用能的符号计算结果相反。自从这一主意被想出来之后——约在1927年,当量子力学开始被理解的时候——许多人就曾做出各种估计和半定量计算,试图得到一个关于λ的理论预言。关于铁里两电子自旋间能量的最新计算——假定该相互作用是相邻原子里两个电子间的一种直接相互作用——仍然会给出错误的符号 。目前对此的理解依旧假定,情况的复杂性不知道是什么原因造成的,并希望下一个根据更复杂情况而进行计算的人能获得正确答案!
目前人们相信,在内壳层上一个造成磁性的电子向上自旋,力图使在外层飞绕的传导电子具有反向自旋。人们也许期待此事会发生,因为那些传导电子已进入与“磁性”电子相同的区域。由于这些传导电子到处运动,它们可以带着其自旋已经颠倒的偏见来到另一个原子附近。这就是说,一个“磁性”电子企图强迫一个传导电子与之反向,此后这传导电子又会促使次一个“磁性”电子与它 反向。这双重相互作用就等效于企图使那两个“磁性”电子平行排列的一种相互作用。换句话说,造成两自旋平行的趋势是由于一种媒介物作用的结果,这媒介物在某种程度上有与两者都相反的倾向。这个机制并不要求传导电子完全“颠倒”过来。它们只可以稍微有些自旋向下的偏向,刚刚足够促使那些“磁性”电子指向另一方向。那些曾经计算过这类事情的人们目前认为这是导致铁磁性的主要原因。但我们必须强调,直到今天还没有人只凭知道该材料在周期表中的数目26就能够算出λ的大小来。总之,我们对它还未充分了解。
现在让我们继续来谈谈这个理论,待以后再回来讨论某一项涉及我们对这一问题的提法上的错误。如果某个电子的磁矩“向上”,则能量既来自外加磁场,也来自使自旋成为平行的那种倾向这两方面。由于当自旋互相平行时能量较低,所以这效应有时被认为是起因于一种“有效内场”。但要记住,这并非 由真实的磁 力引起的,而是一种更为复杂的相互作用。不管怎样,我们把式(37.1)作为关于一个“磁性”电子的两个自旋态的能量公式。在温度T时,这两个态的相对概率正比于e-能量/(kT) ,我们可把它写成e±x ,其中x=μ[H+λM/(∈0 c2 )]/(kT)。这样,若我们计算磁矩的平均值,则会(如同上一章中那样)求得
M=Nμtanhx. (37.2)
现在,我们想要计算材料的内能。我们注意到一个电子的能量恰好与磁矩成正比,因而平均能量的计算就与平均磁矩的计算相同——只要在式(37.2)中μ的地方,我们应该写成-μB也即-μ[H+λM/(∈0 c2 )]。于是平均能量为
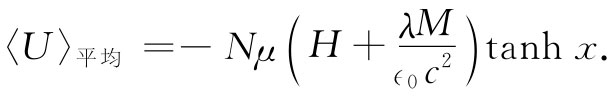
可是这并不是很正确的。由于λM/(∈0 c2 )这一项代表所有可能的原子对 之间的互作用,所以必须记住,每一对只能计数一次 (当我们考虑一个电子在其余电子的场中的能量、而后又考虑第二个电子在其余电子的场中的能量时,我们就已将第一次能量中的一部分多算了一次)。因此,我们就必须将相互作用的项 除以2,于是有关能量的公式结果为

在上一章中,我们曾经发现过一件有趣事情——低于某一温度时,对于该材料人们找到了一个即使没有外加磁化场其磁矩也并不是零 的方程组的解。当我们在式(37.2)中令H=0时,曾求得
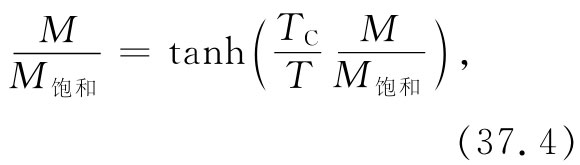
式中M饱和 =Nμ,而TC =μλM饱和 /(k∈0 c2 )。当(用图解法或其他方法)解这一方程时,我们发现,比率M/M饱和 作为T/TC 的函数是一条像图37-1中标明为“量子理论”的曲线。而那条标明为“钴、镍”的虚曲线则表示这些元素晶体的实验结果。理论和实验符合得相当好。在这图上也显示出经典理论的结果,其计算是在假定原子磁体在空间中可以具有一切可能的取向下进行的。你可以看出,这个假定提供了一个甚至不会与实验事实接近的预言。
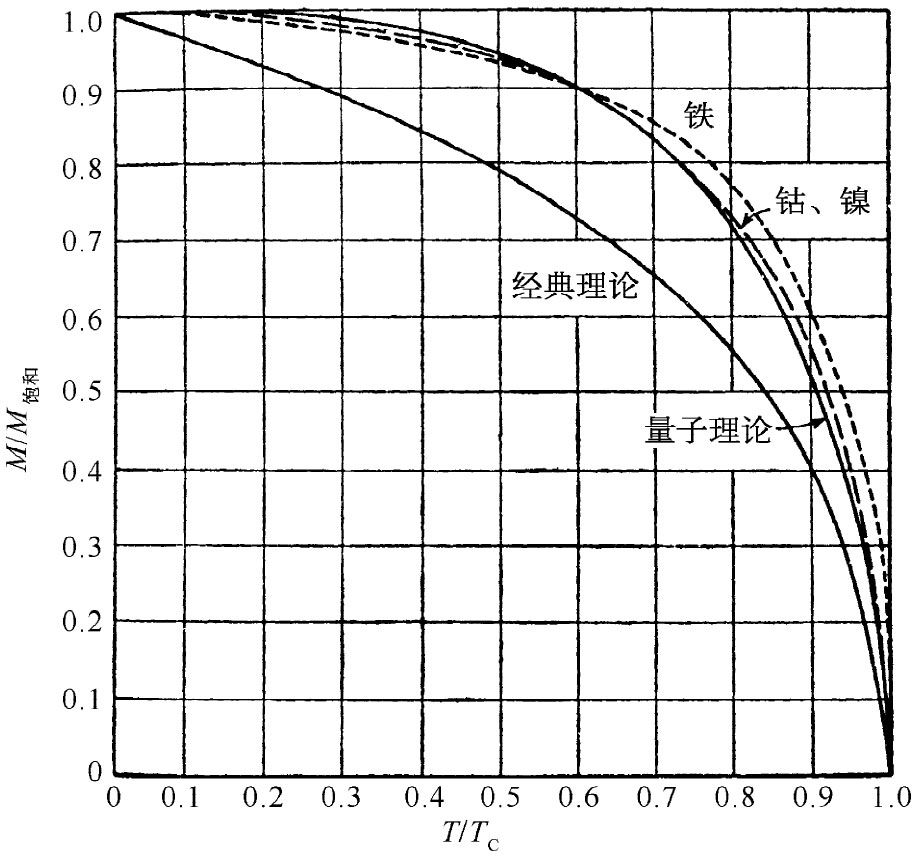
图37-1 铁磁性晶体的自发磁化强度(H=0)作为温度的函数[摘自Encyclopaedia Britannica ]
即使是量子理论,在高温和低温两区域中,也都与所观测到的行为有所偏离。发生偏离的原因是,在该理论中我们曾经做出过一个相当草率的近似:即假定一个原子的能量取决于它的附近原子的平均 磁化强度。换句话说,对于在一给定原子附近的每个“向上”磁矩,就将存在由于那种量子力学排列效应而引起的能量贡献。但究竟有多少个磁矩指“向上”呢?就平均来说,这是用磁化强度M来度量的——不过只是在平均的意义上 而言的。某处的一个特定原子也许会发现它的所有 邻居都是“向上”的。这样,它的能量便会大于平均值。另一个原子可能发现其邻居有些“向上”,而有些“向下”,或许平均为零,因而就该没有来自这一项的能量,如此等等。我们所应当做的是,采用某种较复杂的平均法,因为在不同位置上的原子会有不同的环境,因而对于不同原子就有不同数目的向上和向下的邻居。不仅仅考虑一个受到平均影响的原子,而是应该考虑每一个处于实际情况下的原子,算出它的能量,并求出平均能量 。但我们如何来找出在其附近的原子中究竟有多少个“向上”和多少个“向下”呢?当然,这恰恰就是我们企图要算出的东西——“向上”的和“向下”的数目——因而就有一个十分复杂的相互联系的关联问题,即是一个从未得到解决的问题。这是一个错综复杂而又令人振奋的问题,已存在了许多年,而某些鼎鼎大名的物理学界人士在这方面也曾写过一些论文,但即使是他们也仍未能完全解决该问题。
结果证明,在低温时,当几乎全部原子磁矩都指“向上”而只有少数几个指“向下”时,问题易于解决;而在比居里温度TC 高得多的高温、且它们几乎全都混乱时,问题又容易解决。往往还不难算出在某种简单而又理想的情况下的微小偏差,因而对于为什么会在低温时与该简单理论有所偏离已有相当好的理解。在物理上也已理解到基于统计原因磁化强度应该 在高温时有所偏离。但接近居里点的准确行为就从未被完全算出来过。如果你希望有一个从未被解决的问题的话,则那就是一个有朝一日会计算出来的有重要意义的问题。