
在上一章中,我们已经为计算铁磁性材料的热力学性质打下了必要的基础。自然,这些性质与晶体内能有关,而晶体的内能包括各种自旋的互作用、由式(37.3)给出。对于比居里点为低的自发磁化能量,可以令式(37.3)中的H=0,因而——注意到tanhx=M/M饱和 ——可求得正比于M2 的平均能量:

如果现在把由磁性引起的能量作为温度函数而作图,我们便会得到一条图37-1中那条曲线的平方取负值后的曲线,如图37-2(a)所示。要是此时测量这种材料的比热 ,我们便会得到一条如图37-2(b)所示的曲线,它是图37-2(a)所示曲线的微商。它随温度增加而缓慢地上升,但在T=TC 时就突然降低至零。这一急剧下降是由于磁化能量曲线的斜率刚好在居里点上出现巨大改变引起的。因此,完全不需要任何磁性测量,根据测量这一热力学性质,我们就可以发现在铁或镍中将发生的某些事情。然而,实验和经过了改进的理论(包括涨落)却都显示这条简单的曲线是错误的,而真实的情况实际上更加复杂。该曲线在那尖峰处升得更高,而下降至零时则有点缓慢。即使温度已高至足以在平均上 使自旋处于混乱状态,但是仍然会有局部区域存在某些磁化量,而在这些区域中自旋具有小的额外相互作用能——这只有在温度进一步升高而情况变得越来越混乱时才会缓慢地消失。因此,实际的曲线看来就像图37-2(c)那样。今天理论物理学的挑战之一就是要找出在居里转变点附近关于比热特性的准确的理论描述——一个还未得到解答的引人入胜的问题。自然,这个问题与同一区域内磁化曲线的形状会有十分密切的关系。
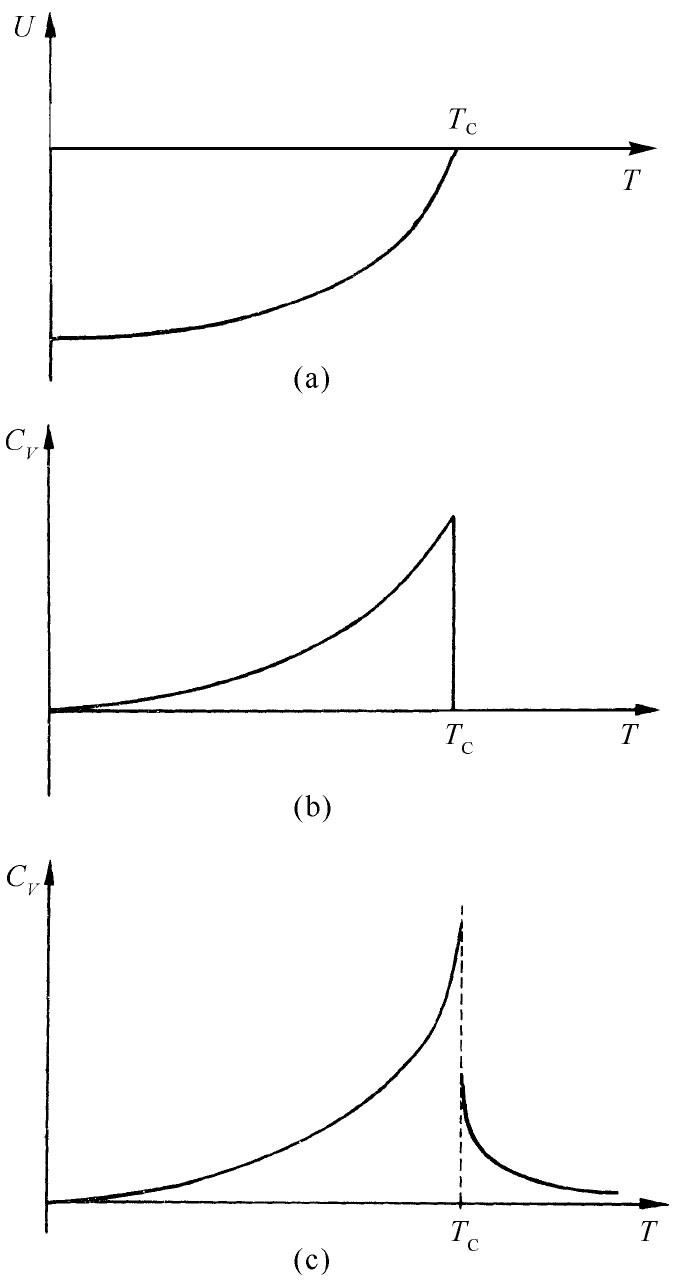
图37-2 一块铁磁性晶体的单位体积能量和比热
现在要来描述某些除热力学以外的实验,这些实验会证明,我们对磁性的解释有些是正确的 。当材料在低温下被磁化至饱和程度时,M很接近于M饱和 ——几乎所有自旋以及它们的磁矩都是平行的。这可以通过下述实验加以核实。假设将一条形磁铁用一根细丝悬挂起来,然后对它包围上一个线圈,使得无需接触磁铁或对其施加任何转矩就能使磁场倒转过来。这是一个十分难做的实验,因为磁力如此巨大以致任何不平衡、任何倾斜或在铁里的任何不完整都会产生一些偶然的转矩。然而,该实验已在这种偶然转矩被减至最低程度的小心谨慎条件下完成了。利用包围在磁铁上的那个线圈的磁场,我们一下子就将所有的原子磁体全都翻转过来了。当我们这样做时,也将所有自旋的角动量都由“向上”变成了“向下”(见图27-3)。如果在这全部自旋都翻转过来时角动量守恒,则铁条的其余部分就必然在角动量方面有相反的改变,整块磁体将开始旋转。果然,当我们做这一实验时,就发现磁铁的微小转动。可以测出给予整条磁铁的总角动量,而这仅是N乘以ћ,后者为每个自旋角动量的变化。由这样量得的角动量与磁矩的比率同我们的计算值相差约在10%以内。实际上,我们的计算曾假定原子磁体纯粹起因于电子自旋,但在大多数材料中除了自旋之外,还有某种轨道运动。由于这种轨道运动不是完全脱离晶格的,因而对于磁性的贡献就不会超出百分之几很多。事实上,通过取M饱和 =Nμ及利用铁的密度为7.9和自旋电子的磁矩μ,人们所得到的饱和磁场约为20000Gs。但根据实验,它实际上是在21500Gs左右。这是误差的典型值——5%~10%,由于忽略了包含在所做的分析中的轨道磁矩的贡献造成的。于是,上述回转磁测量中的微小偏差就完全理解了。
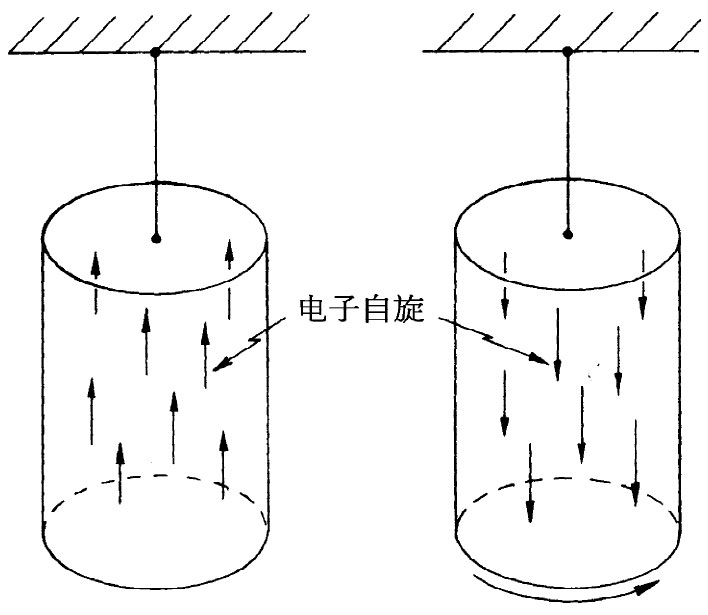
图37-3 当铁条中的磁化方向倒转过来时,铁条会得到某一角动量