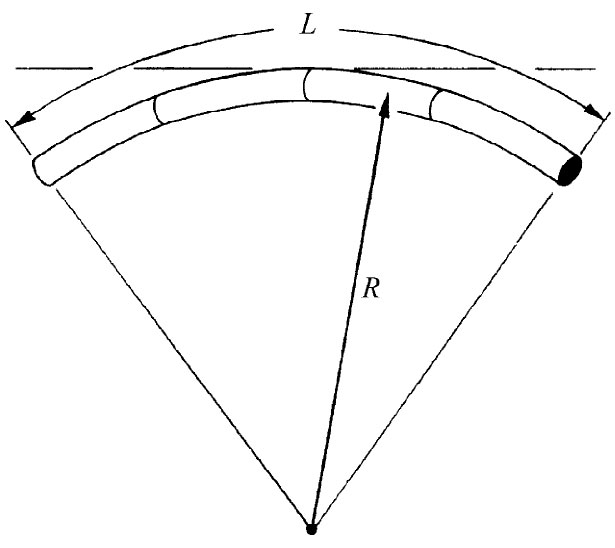
图38-11 一根弯曲的梁
现在要来考察另一个实际问题——棒或梁的弯曲 。当我们弯曲一根具有任意截面的棒时，力会怎么样呢？虽然我们将算出的是设想的一根具有一圆截面的棒，但其答案将适用于任何的形状。然而，为了节省时间，我们将抄近路，因而即将得到的理论仅仅是近似的。我们的结果将只在弯曲的半径比梁的厚度大得多时才正确。
假定你抓住一根直棒的两端而把它弯成像图38-11那样的曲线，在该棒内部会发生什么情况呢？噢，如果它被弯曲了，则意味着在该曲线之内的材料受到压缩，而在曲线之外的材料受到拉伸。存在某一个近似与棒轴平行的面既不被拉长也不被缩短，这个面叫做中性面 。你会预期，这个面靠近横截面的“中间”。可以证明（但我们将不在这里做出）：对于简单梁的微小弯曲，中性面会穿过横截面的“重心”。这只有对于“纯”弯曲——只要你不同时对梁拉伸或压缩——才正确。
图38-11 一根弯曲的梁
这样，对于纯弯曲来说，梁的一块横向薄片就会如图38-12（a）所示的那样变形。在该中性面之下的材料具有与距这一中性面的距离成正比 的压缩应变；而在其上的材料则被拉伸，其应变也正比于距这一中性面的距离。因此，纵向伸长 Δl与高度y成正比，其比例常数恰好就是l除以该棒的曲率半径——参见图38-12：
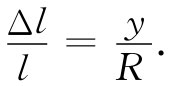
所以在y处的一条小带上单位面积的力——应力——也与距中性面的距离成正比：
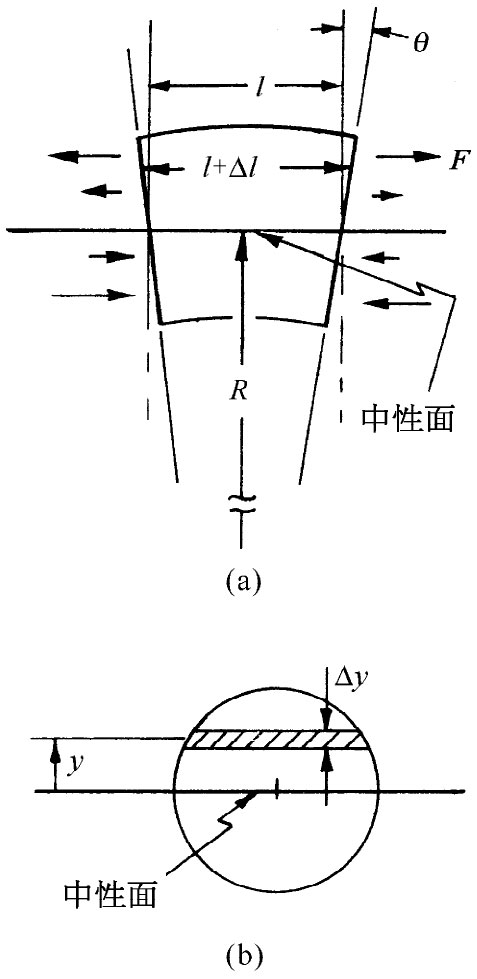
图38-12 （a）一根弯曲梁中的一小片段；（b）梁的横截面
现在让我们来考察这一应变产生的力
。作用于图38-12中那一小段上的各个力如图所示。如果设想任何横向截面，则作用于其上的力在中性面之上朝一个方向，而在中性面之下则朝另一个方向，它们成对地构成一个“弯曲转矩”
——这指的是绕该中性线的转矩。我们可通过对图38-12中那样一小段的一个面上的力乘以距中性面的距离，然后进行积分，从而计算出总转矩：
（38.35）
根据式（38.34），dF=（Yy/R）dA，因而
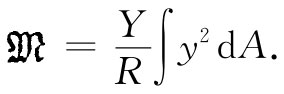
y2 dA的积分我们可称之为该几何截面绕穿过其“质心”的水平轴的“转动惯量” [2] ，我们将把它叫作I：
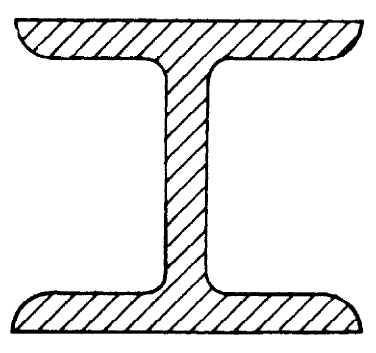
于是，式（38.36）向我们提供了有关弯曲转矩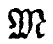
与梁的曲率1/R之间的关系。梁的“刚度”与Y和转动惯量I均成正比。换句话说，如果你要用比如说一定数量的铝来制造一根尽可能强硬的梁，那你就得把尽可能多的铝放在离中性面较远的地方，以便造成一个大的转动惯量。然而，不能把此推至极端，因为这么一来该件东西就将不会如我们所假定的那样弯曲——但却将弯折或曲折，因而又会变成较脆弱了。可是现在你已明白，为什么结构梁要造成工字形或H字形——如图38-13所示的那样。
|
|
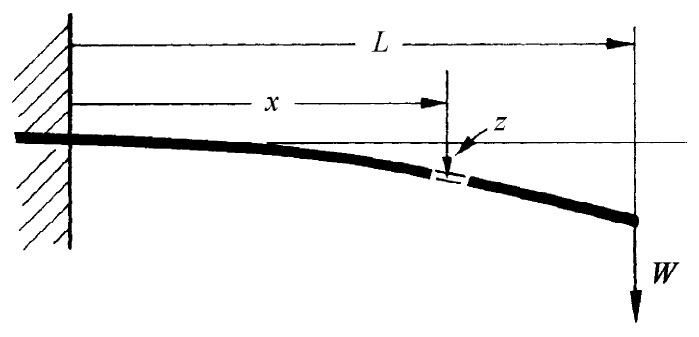
| 图38-13 “工字”梁 | 图38-14 一端加有重量的一根悬臂梁 |
作为梁方程式（38.36）的一个应用例子，让我们算出有集中力W作用于其自由端的一根悬臂梁的偏离，如图38-14所示意的那样（所谓“悬臂”我们只是指梁被支持得使其一端的位置和 斜率都保持固定——它被插入水泥墙内）。这根梁的形状将会怎么样呢？让我们把距固定端的距离为x处的偏离量叫作z，我们希望知道z（x），将只对小的偏离作出计算，也将假定与其截面比较起来梁是很长的。现在，正如你已从数学课中懂得，任一条曲线z（x）的曲率1/R由下式给出：
由于我们只对于小斜率感兴趣——这往往是工程结构中的情况——与1比较起来略去（dz/dx）2 ，从而取
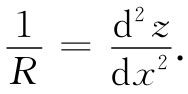（38.39）
我们也需要知道弯曲转矩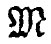
，它是x的函数，因为它等于绕任一个横截面的中性轴的转矩。让我们略去梁本身的重量而仅仅考虑在梁末端处向下的力W（如果你愿意的话，可以把梁的重量也考虑进去）。于是在x处的弯曲转矩为
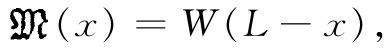
因为那是由重量W所施加的、围绕着x点的转矩——梁必须在x处加以支撑的转矩。我们就得到
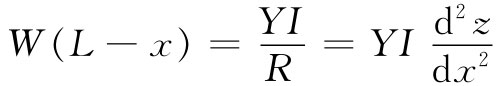
或
这是一个没有什么窍门的、可以积分的方程，结果得到
这里利用了在x=0处z（0）=0及dz/dx也等于零的假定。那是由梁的形状决定的。末端的位移为
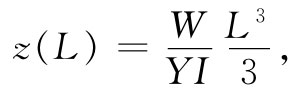（38.42）
即一根梁末端的位移随长度的立方而增加。
上面在导出梁的近似理论时，我们曾经假定过梁的横截面在梁被弯曲时不会改变。当梁的厚度与曲率半径相比显得微小时，因横截面的改变非常小，所以我们的结果是好的。不过，一般说来，这一效应是不能忽略的，正如你能够通过把一块软橡皮擦弯曲在手指上而容易自行验证出来那样。如果原来的横截面是一个矩形，你将会发现，当它被弯曲时在其底部会凸起来（见图38-15）。此事之所以发生，是因为当我们推压其底部时，材料便向旁延伸——正如由泊松比所描述的那样。橡皮是容易弯曲或伸长的，但它有点像液体，即很难改变其体积 ——犹如你在弯曲那块橡皮擦时它所明白表现出来的那样。对于不可压缩的材料，泊松比应该恰好等于1/2——橡皮几乎就是这样。
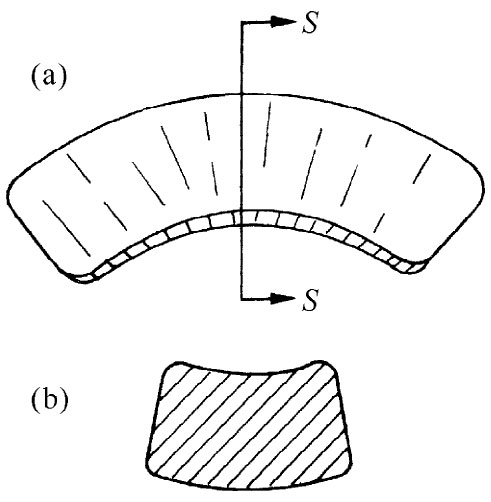
图38-15 （a）一块被弯曲的橡皮擦；（b）横截面