上一章我们曾谈到一些特殊弹性体的形变，本章我们将要考察弹性材料内部通常 可能发生的情况。我们希望当用某种复杂方式把一大团果子冻扭转和压缩时，有可能描述其内部的应力和应变的情况。要完成此事，就需要能描写弹性体中每一点上的局域应变 。对此，我们可以通过对每一点给出一组六个数——一个对称张量的分量——来做到。以前我们就曾谈及应力张量（第31章），现在却需要应变张量。
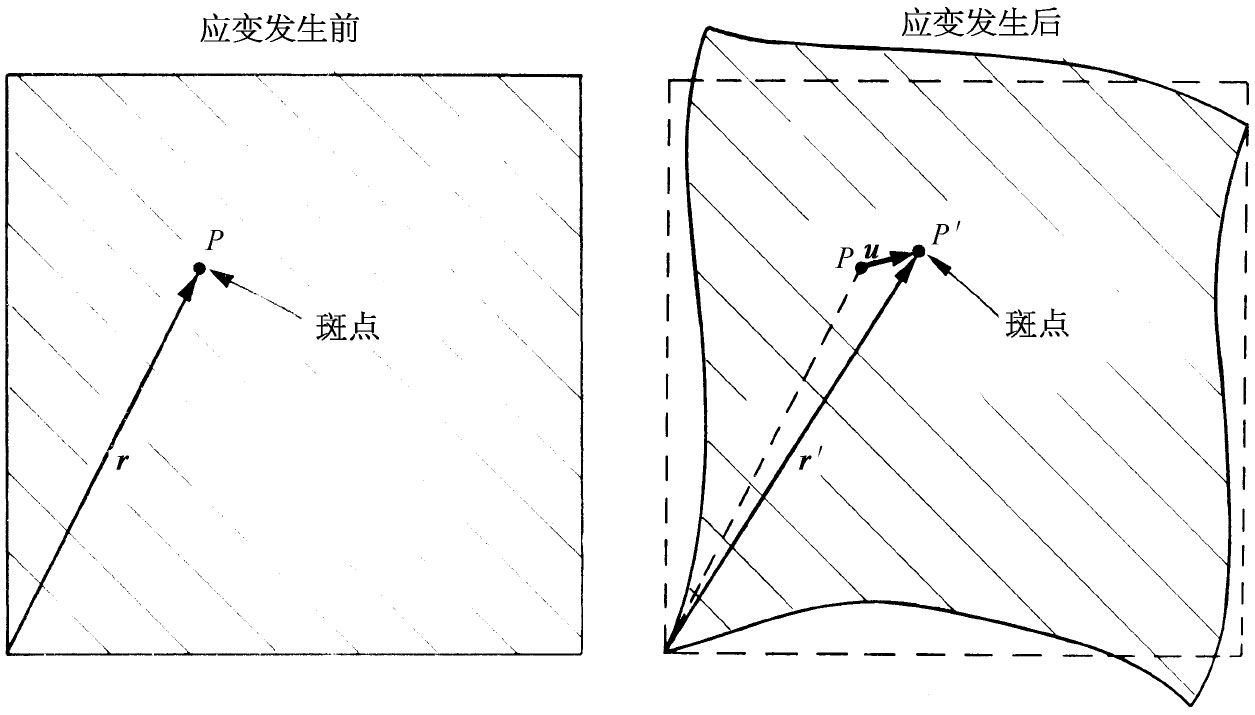
考虑从一块起初未发生任何应变的材料出发，并注意当其发生应变时埋在材料里的一个小“灰尘”斑点的运动。原来被放在P点、即r=（x，y，z）处的斑点，移到如图39-1所示的P′点、即r′=（x′，y′，z′）处。我们把从P至P′的矢量位移记作u。于是
u=r′-r. （39.1）
当然，这位移u依赖于我们出发的一点P，因而u就是r的一个矢量函数——或者，如果你喜欢的话，也即是（x，y，z）的函数。
图39-1 在未发生应变的一块材料中位于P点处的斑点，当材料发生应变后移到P′点处
让我们首先来考察应变在整块材料中是常数的那种简单情况——因而我们就有所谓均匀应变 。例如，假设有一块材料，将其均匀拉伸，仅仅在一个方向——比如在x方向——上均匀地改变它的长度，如图39-2所示。位于x处斑点的位移ux 与x成正比。实际上，我们将ux写成这样：
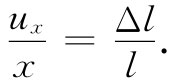
ux =exx x.
当然，比例常数exx 与Δl/l是同一件事（你不久就会看到为什么我们要用一个双重脚标）。
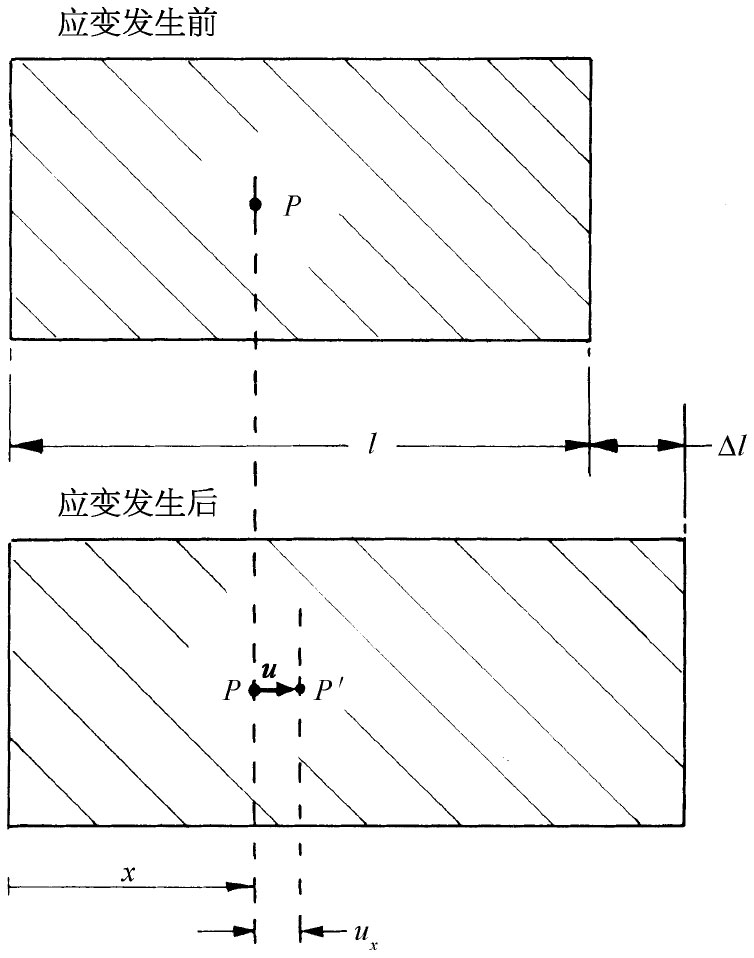
图39-2 均匀拉伸型应变
如果应变不均匀，则ux 与x的关系将在材料里逐点改变。对于一般的情况来说，就要用一种局域的Δl/l，即用下式来定义exx ：
exx =∂ux /∂x. （39.2）
这个数——它现在是x，y和z的函数——描述整块果子冻中x方向的伸长量。当然，此外还可以有沿y向和z向的伸长，我们用下列两个数值来描述：
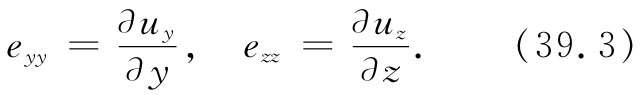
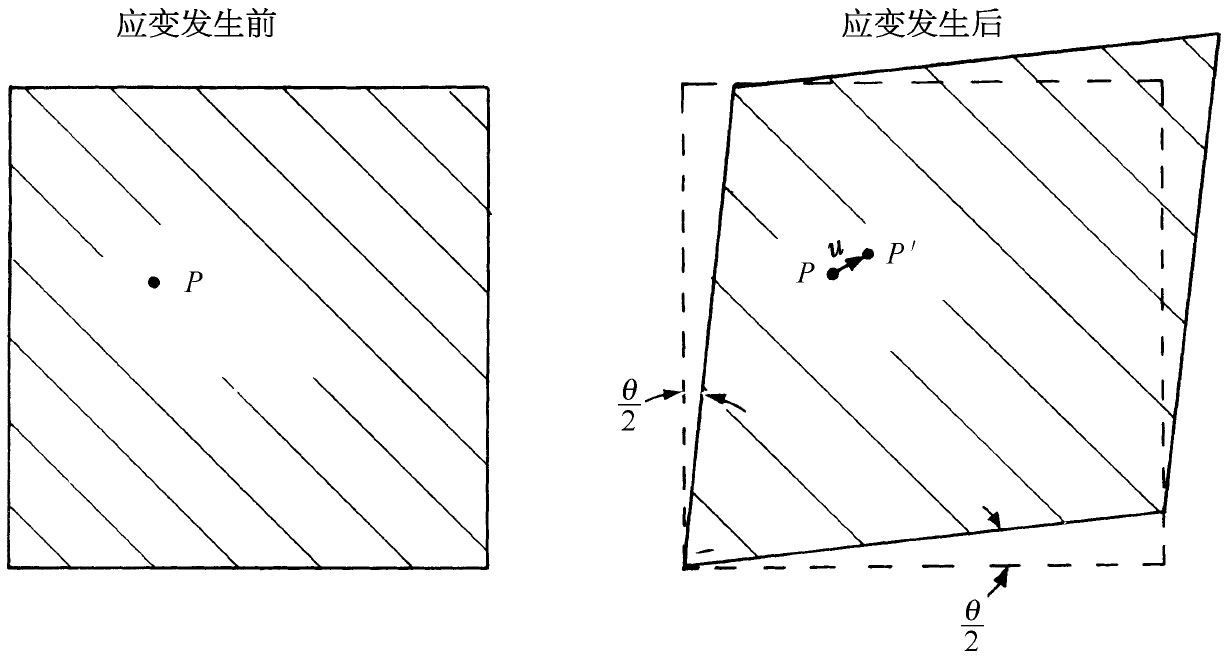
图39-3 均匀剪切应变
我们也需要能描述剪切型的应变。假设我们想象在起初未发生形变的果子冻中标示出一个小立方体。当这团果子冻被推压而变形时，立方体的一个面可能变成一个平行四边形，如图39-3所示意的那样 [1] 。在这种应变中，每个质点在x方向的移动与y坐标成正比，
（39.4）
还有一个正比于x的y方向的位移，
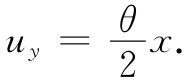（39.5）
因此，我们就能够通过写出
ux =exy y， uy =eyx x，
其中
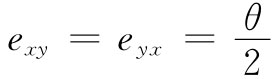
来描述这种剪切型应变。
现在你也许会想到，当应变不均匀时，我们可以用下面对exy 和eyx 这两个量所下的定义来描述普遍的剪切应变：
不过这里有一点困难。假定位移ux 和uy 分别由下式给出：
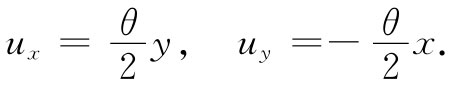
除了uy 的符号相反之外它们就很像式（39.4）和（39.5）。对于这些位移来说，果子冻中一个小立方体将仅仅转过一个角度θ/2，如图39-4所示。完全没有什么应变——只不过在空间中的转动，材料没有变形，所有原子的相对 位置都根本没有改变。所以应当想办法使纯转动不包括在我们对剪切应变的定义之中。关键点在于：若∂uy /∂x和∂ux /∂y相等而相反，则没有应变，因此，我们可用下列定义 解决问题：
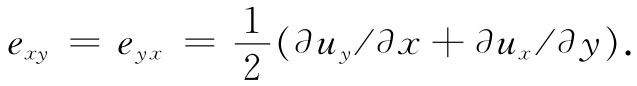
对于纯转动来说，两者均等于零，但对于纯剪切则会得到exy 等于eyx ，这正是我们想要的那种关系。
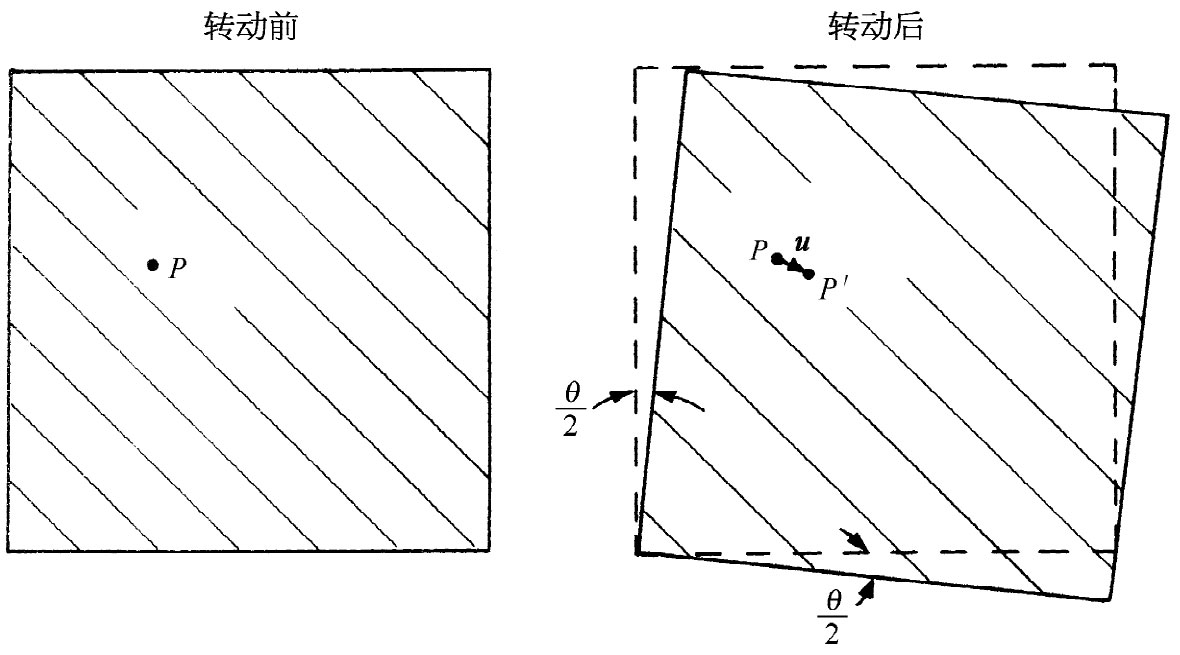
图39-4 均匀转动——没有应变
在最普遍的形变中——可以包括伸长或收缩以及切变在内——我们可通过给出九个数值来定义 应变态：
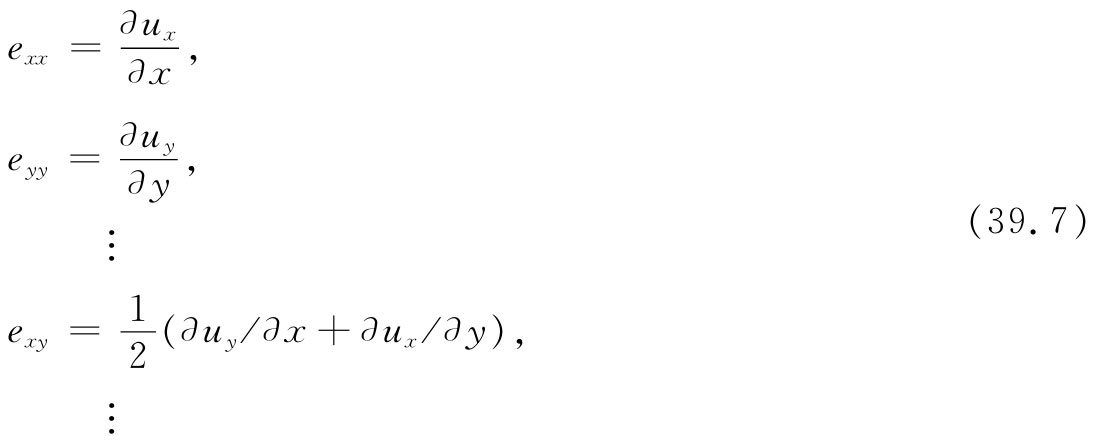
这些就是应变张量 的各项。由于它是一个对称张量 ——我们的定义总是使得exy =eyx ——实际上，它只有六个不同的数。你会记得（见第31章），张量的普遍特征是：那些项都会像两个矢量的分量之积那样变换（若A和B都是矢量，则Cij =Ai Bj 便是一个张量）。eij 的每一项都是矢量u=（ux ，uy ，uz ）和算符▽=（∂/∂x，∂/∂y，∂/∂z）的各分量之积（或这种积之和），我们知道后者如同一个矢量那样变换。让我们令x1 ，x2 ，x3 各代表x，y，z，而u1 ，u2 ，u3 各代表ux ，uy ，uz ，则可以将这个应变张量的普遍项eij 写成
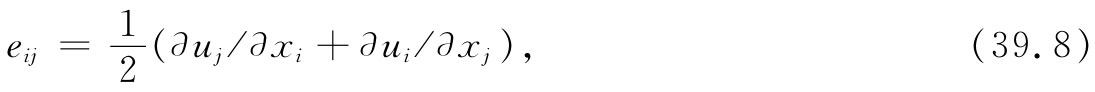
式中，i和j各可以是1，2或3。
当有一均匀应变——可以包括拉伸和剪切——时，则所有的eij 都是常数，因而可以写出
ux =exx x+exy y+exz z （39.9）
（我们选取u为零的那一点作为x，y，z坐标系的原点）。在这种情况下，应变张量eij 会给出坐标矢量r=（x，y，z）和位移矢量u=（ux ，uy ，uz ）之间的关系。
当应变不均匀时，果子冻的任一部分也可能受到一些扭转——会存在局域转动。若形变都很小，则应该有
式中ωij 是一个反对称 张量，
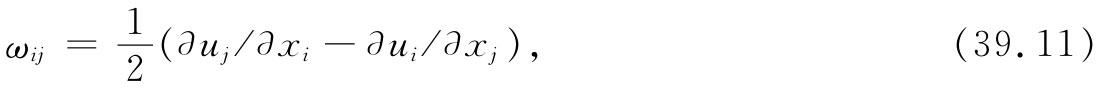
上式能够描述转动。可是，我们将不再为转动操心，而仅关心由对称张量eij 描述的应变。