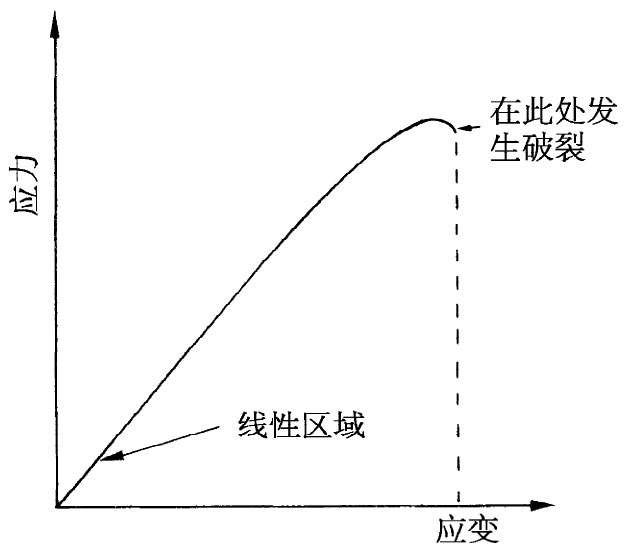
图39-8 大应变的一个典型应力应变关系
迄今在我们所谈及的一切情况中都曾假定应力正比于应变;一般说来,这是不 正确的。图39-8显示一种可延性材料的典型应力-应变曲线。对于小应变来说,应力与应变的确成正比。可是,最后当越过了某一点之后,应力与应变的关系就开始与直线有所偏离了。就许多种——我们总称之为“脆性”的——材料来说,只要应变稍微超过该曲线开始弯下去的一点,物体就会破裂。一般说来,在该应力应变关系中还有其他复杂性。例如,若你使一物体变形,则应力最初可能会很高,但随着时间推移应力会慢慢降低。而且,如果已达到了高的应力,但还未达到“破裂”点,则当你减少应变时,应力将会沿另一条曲线返回。即有一个小小的滞后效应(类似我们在磁性材料中见到的B和H间的关系曲线)。

图39-8 大应变的一个典型应力应变关系
材料将会破裂的那个应力,一种材料与另一种材料的差异很大。有些材料在最大拉伸 应力达到某一定值时发生断裂,另一些材料则会在最大剪切 应力达到某一个值时破裂。粉笔是一种张力比剪切力弱得多的材料的例子。如果你拉一支粉笔的两端,粉笔将在垂直于所加应力的方向上断裂,如图39-9(a)所示。之所以在垂直于外加力的方向上断裂,是由于粉笔不过是一群易于拉开的粒子被紧压在一起而已。然而,这一材料却难于发生切变,因为其中粒子会彼此互相妨碍。现在你会记起,当有一根棒处于扭转中时,则环绕着它各点都存在剪切力。并且,也曾经证明过,剪切应力等效于拉伸应力与压力在45°角上的组合。由于这些原因,如果你扭转 一支黑板上用的粉笔,它将沿着与轴成45°角开始的一个复杂的面破裂。一支这样破裂了的粉笔的照片如图39-9(b)所示,粉笔是在拉伸应力最大的地方破裂的。

图39-9 (a)两端受拉力而断裂的一支粉笔;(b)因扭转而断裂的粉笔
别的材料表现出奇特而复杂的行为。材料越复杂,其行为就越发有趣。如果取一条莎纶头巾,把它揉皱成一团,并将其投掷到桌面上,则它将会缓慢地自己舒展开来从而恢复它原来的平坦形式。乍看起来,我们也许总会以为是惯性在阻碍着它回复原来的形状。然而,简单的计算表明,惯性对于解释该效应小了好几个数量级。似乎存在两种重要的互相对抗的效应:材料内部“某种东西”会“记得”它原先有过的形状,并“力图”恢复原样;但另外某种东西“更喜欢”新的形状,而“阻止”回到原先的形状上去。
我们将不尝试去描写莎纶塑料中起作用的那种机制,但你可从下述模型 中获得关于这种效应怎么可能发生的一些概念。假设你想象一种材料,它由长而柔顺但却坚韧的纤维与充满着黏滞性液体的某些小孔互相混合在一起而构成。也想象从一个孔到邻近的孔存在一些狭窄的通道使得液体能够从一个孔缓慢地渗入邻近的孔。当我们揉皱一片这样的材料时,使那些长纤维变了形,把在一处小孔里的液体挤压出来而逼进到那些正被拉伸着的其他小孔中去,在我们把那片材料释放后,长纤维会试图恢复它们原来的形状。但这样做时,必须迫使液体回到原先的位置上去——由于黏滞性的缘故这将进行得相当慢。在我们将该片东西揉皱时所加之力,比起由那些纤维所施之力要大得多。我们能够迅速地将其揉皱,但恢复的过程就较为缓慢了。这无疑是那些大而强硬的分子与一些较小而易移动的分子在莎纶头巾中的组合是造成它行为的主要原因。这一概念也符合下列事实:材料在温暖时会比寒冷时更迅速地恢复到它原来的形状——热量增加了较小分子的可动性(降低了黏滞性)。
虽然我们刚才正在讨论胡克定律为何会失灵,但引人注目之处或许不是胡克定律对于大的应变会发生失灵,而是它总是很普遍地成立。我们通过考察材料中的应变能量可以获得这事情为什么会这样的某些概念。提出应力正比于应变,同提出应变能量随应变的平方而变化,是同一回事。假设把一根棒扭转了小角度θ,如果胡克定律正确,则应变能量应当与θ的平方成正比。如果我们假定这个能量为旋转角度的任意函数,那就可以把它写成关于零角度的泰勒展开式:
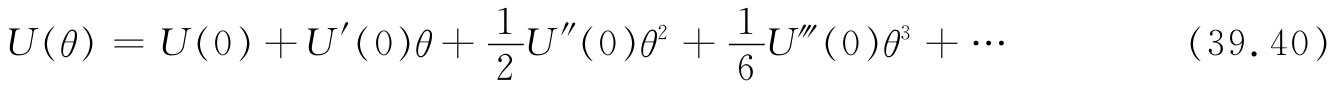
转矩τ等于U对角度的微商,我们应有
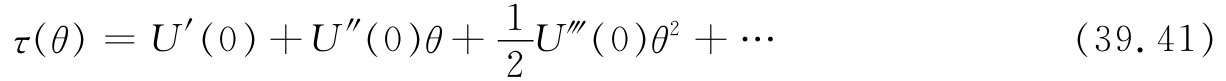
现在,若从那平衡 位置度量我们的角度,则第一项为零,因而第一个留下的项是与θ成正比的。而对于足够小的角度,它将比含θ2 的项占有明显优势[事实上,材料内部是足够对称的,以致τ(θ)=-τ(-θ),于是这个含θ2 的项便将为零,因而与线性的偏离就只会来自那θ3 的项了。然而,为什么这对于压缩和伸张都应该正确,就找不出理由来了]。我们还未加以解释的事情在于,为什么材料往往会在那些高阶项变得重要之后就立即断裂。