流体,特别是水的流动这一课题使每个人都着迷。我们均能记起自己小时候,在澡盆里或在泥浆水坑里与那种奇怪的东西玩耍。当我们逐渐长大时,便会注视着河流、瀑布以及旋涡水塘,因而被这种相对于固体来说似乎像是活生生的物质所迷住。流体的行为在许多方面都很出人意外并且十分有趣——它是本章和下一章的课题。在街上一个小孩子企图阻塞一股小水流的努力,以及他对水确定它的道路的那种奇特方式所感到的惊异,与我们多年来为理解流体流动所做的努力很类似。我们试图依靠获得的描述流动的那些定律和方程式——以我们的理解——来筑坝拦水。我们将在这一章中描述这些尝试。而在下一章中,将描述水如何会冲出水坝以及使我们理解它的努力落空的那种独特方式。
假定你们都已熟悉了水的基本性质。区别流体与固体的一个主要性质就是流体不能维持 任意长的时间切应力。如果我们对流体作用一剪切力,则它将在这剪切力作用下运动。像蜂蜜那样较稠的液体,比起像空气或水的流体来就不那么容易流动。对一流体量度其屈服的难易程度的乃是它的黏滞性。在本章中,我们将只考虑其中黏滞效应可以忽略的那些情况,黏滞效应将在下一章中考虑。
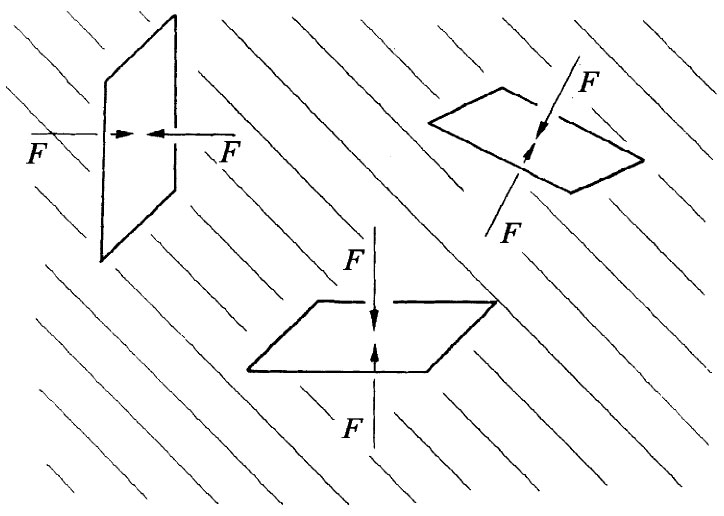
我们将从考虑流体静力学 ,即静止时的流体理论开始。当流体静止时,就没有任何剪切力(甚至对于黏滞性液体亦然)。因此,流体静力学的定律是:应力总是垂直于流体内的任何一个面。单位面积的这个法向力叫做压强 。从静止流体中不存在剪切力这一事实出发,就可以推断出压应力在所有方向都相等(图40-1)。我们将让你们自己娱乐一下,即证明若在流体中的任一个面上都没有剪切力,则压强在任何方向必然相同。

图40-1 在一静止流体中,作用于任何截面上的单位面积的力与该面垂直,并且对于面的所有取向都相同
流体中的压强可以逐处变化。例如,在地球表面的静流体中,压强将由于流体的重量而随高度变化。如果该流体的密度被认为不变,并且如果把某个任意零水平面处的压强称为p0 (图40-2),则在水平面以上高度为h处的压强就是p=p0 -ρgh,其中g为单位质量的重力。因此,组合
p+ρgh
在静止流体中是一恒量。这个关系式是你们熟悉的,但现在要来导出一个把上式作为一种特殊情况的、更为普遍的结果。
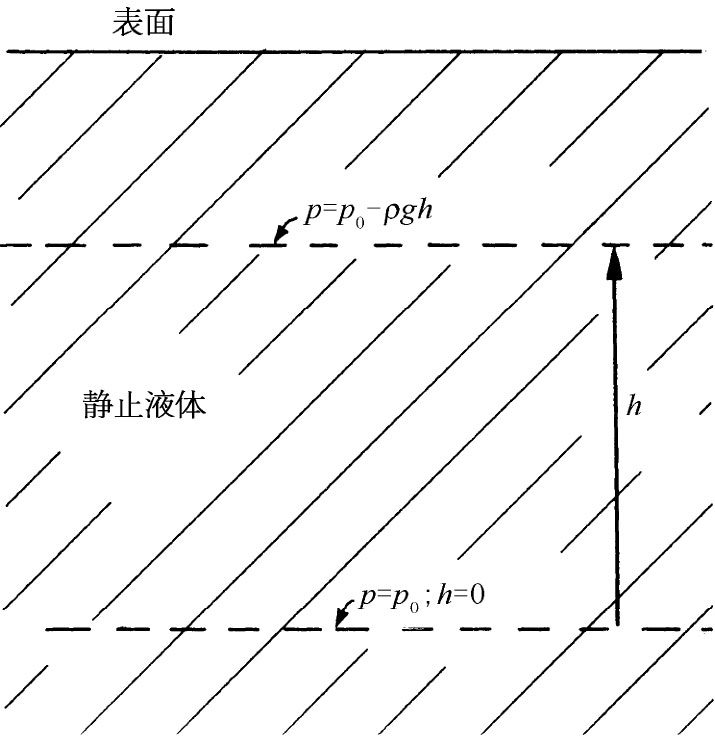
图40-2 在一静止液体中的压强
如果考虑水的一个小立方体,那么作用于其上的来自压强方面的净力是什么呢?因为在任何地方压强在各个方向都相同,所以仅由于压强的逐点变化就能够产生单位体积中的净力。假设压强在x方向上是变化的——而我们所选取的各坐标轴方向都平行于该立方体的各边。这样作用于x处面上的压强就会提供pΔyΔz的力(图40-3),而在x+Δx处面上的压强则提供-[p+(∂p/∂x)Δx]ΔyΔz的力,因而净力为-(∂p/∂x)ΔxΔyΔz。如果我们考虑这一立方体的其余各对表面,则不难看出,单位体积的压力为-▽p。若除此之外还有别种力——诸如重力——则该压力就必须抵消它们才能得到平衡。
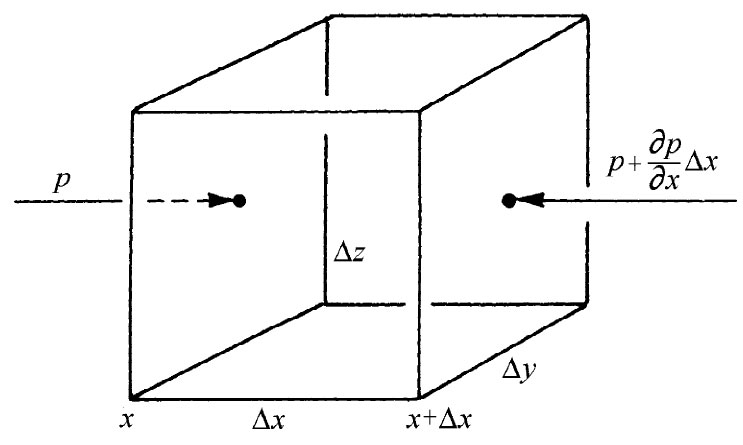
图40-3 作用于立方体上的净压力为单位体积的-▽p
让我们考虑这种附加力可以由一势能来加以描述的情况,就像在重力情况下它应该是正确的那样,我们将令ϕ代表单位质量的势能(比如,对于重力,ϕ就恰好是gz。)单位质量的力通过-▽ϕ用势表出,因而若ρ为流体密度,则单位体积中的力就是-ρ▽ϕ。对于平衡的情况来说,单位体积的这种力加上单位体积压强方面的力就必然为零:
-▽p-ρ▽ϕ=0. (40.1)
式(40.1)就是流体静力学的方程。在一般 情况下,它没有解 。若密度在空间中按任意方式变化,就没有办法使得这些力互相抵消,因而该流体就不可能处于静平衡之中。此时对流将开始出现。我们从这一方程就可以清楚地看出,因为压强项是一纯粹梯度,而对于可变的ρ那里的另一项并不是梯度。只有当ρ是常数时,该势能项才是纯粹梯度。此时方程就有解
p+ρϕ=常数.
另一种容许流体静力平衡的可能性是,ρ仅为p的函数。然而,我们将放下流体静力学这一课题,因为它与流体运动时相比远不是那么有趣。