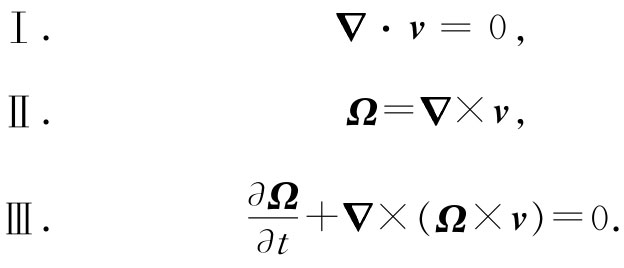
对于可能有涡旋的不可压缩流体,其流动的一般方程式为
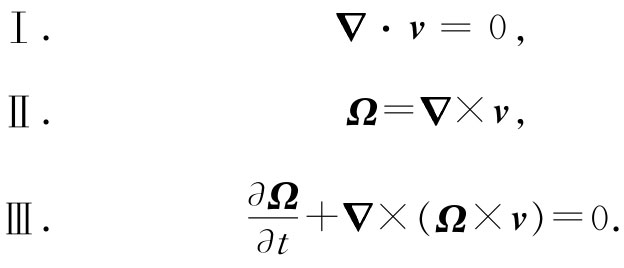
这些方程的物理内容曾由亥姆霍兹通过三个定理用语言描述过。首先,设想在流体中我们应该画出涡线 而不是流线。所谓涡线,指的是具有Ω的方向、并在任何区域里都具有与Ω的大小成正比的密度的那种场线。根据上列方程Ⅱ,Ω的散度始终 等于零(回忆起§3-7中旋度的散度总是零)。因此,涡线就像B线,它们从来既没有始点也没有终点,因而往往会形成闭合回路。现在亥姆霍兹通过下述这一句话来描述Ⅲ:涡线随流体一起在运动 。这意思是:假如你对沿某些涡线的流体质点加以标志——比如用墨水给它们着色——那么当流体带着那些质点一起运动时,它们将始终标志着那些涡线的新位置。无论流体中的原子怎样运动,涡线总是跟着它们一起前行。这是描述那些定律的一种方法。
它也提供了求解任何问题的一种方法。给出最初的流动图样——比如,各处的v值——那么你便可以算出Ω来。根据v你也可以讲出在一会儿之后那些涡线将会跑到哪里——它们以速率v运动。用新的Ω,你便可以应用方程Ⅰ和Ⅱ求出新的v(这很像给定电流后求B的问题)。如果我们得到了某一时刻的流动图像,则在原则上就可以算出后来一切时刻的图像。因此我们就得到关于非黏滞流动的一般解。
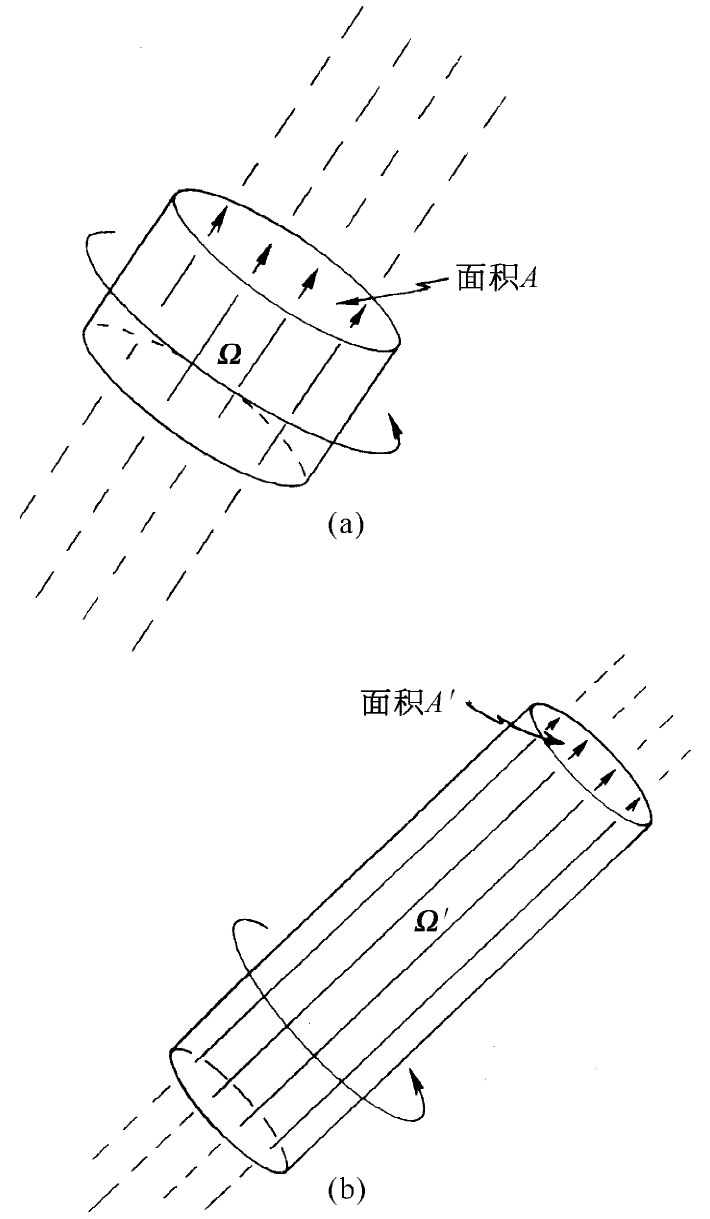
图40-13 (a)在t时刻的一群涡线;(b)同一群线在较迟的t′时刻
现在要来说明:亥姆霍兹的表述——因而也就是Ⅲ——如何才能够至少部分地加以理解。实际上它仅仅是应用于流体的角动量守恒定律。试设想一个其轴平行于涡线的液态小柱体,如图40-13(a)所示。在此后某一时刻,这同一 块流体将移至别处。一般说来,它将占据一个直径不同的柱体并将位于不同的地方。它也可以有不同取向,比如图40-13(b)所示的那样。但是,若直径已经变小,则长度就会增长,以保持其体积不变(因为我们假定的是一种不可压缩的流体)。并且,由于涡线离不开材料,所以其密度就会随截面的缩小而增大。涡度Ω与该柱体的截面积A两者之积将保持不变,因而按照亥姆霍兹表述,应有
Ω2 A2 =Ω1 A1 . (40.21)
现在要注意:由于黏滞性为零,因而所有作用于该柱体(就那事来说,或任何 体积)的表面上的力就都垂直于该表面,这种压力能够导致该体积从一处移至另一处,也能使它改变形状,但由于没有切向 力,所以材料内部的角动量 的大小就不可能改变。该小柱体内液体的角动量等于其转动惯量I乘以液体的角速度,它正比于涡度Ω。对于柱体来说,转动惯量正比于mr2 。因此根据角动量守恒,我们就应该断定
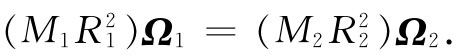
可是质量彼此相同,即M1 =M2 ,而截面积则正比于R2 ,因而我们又再次得到方程式(40.21)。亥姆霍兹的表述——与Ⅲ等效——正好是在没有黏滞性的条件下流体元的角动量不可能发生改变这一事实的推论。
有一个用图40-14所示的简单设备形成运动涡旋的精彩演示。用一张绷紧的厚橡胶膜覆盖在一个柱形箱的开端上构成一个“鼓”,鼓的直径2ft,深也是2ft。鼓“底”——这个鼓被翻倒而靠它的侧壁支持着——除了有一个直径3in的孔外,周围都密闭。如果你用手在橡胶膜上猛击一下,一个涡环就被从孔中投射出来。尽管涡旋看不见,但你却能说出它在那儿,因为它会吹熄放在10~20ft远处的一支蜡烛。根据这一效应的迟延时间,你可以说出“某种东西”正在以一有限的速率行进着。如果你先将一些烟雾吹进箱子里,则还能对发生的情况看得更清楚。这时你会把涡旋看成一个美丽的圆“烟环”。
图40-14 造成一个正在移动的涡环
烟环是环状的涡线群,如图40-15(a)所示。由于Ω=▽×v,这些涡线也代表图(b)中的v的环流。我们可以按照下述办法来理解烟环的前进运动:环底 附近的环流速度会延伸到环顶,而那里就有一个前进运动了。由于Ω线同流体一起运动,这些线也就以速度v向前运动(当然,环顶部附近的v的环流导致底部的涡线的向前运动)。
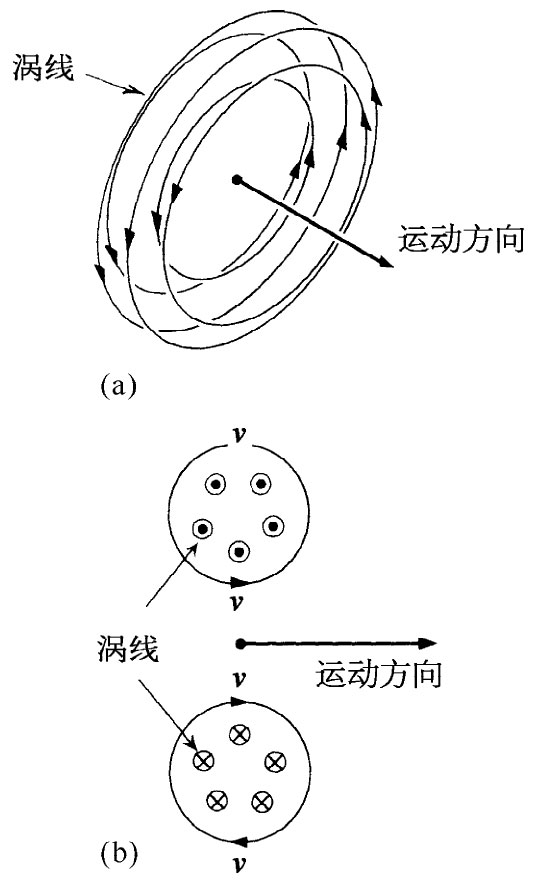
图40-15 一个运动着的涡环(烟环)。(a)涡线;(b)涡环的截面
现在必须提到一个严重的困难。我们已经注意到式(40.9)表明:若Ω起初为零,则它将永远为零。这个结果表明“干”水理论的大失败,因为它意味着,一旦Ω为零,则它将永远 为零——在任何场合下都不能产生 任何涡度。可是,在我们利用那个鼓的简单演示中,却能够从原来是静止的空气里产生出涡环来(肯定在我们击鼓以前,鼓箱里处处都是v=0,Ω=0)。并且,我们全都知道,可以在湖水中用一柄桨来发生一些涡旋。显然,必须研究“湿”水的理论才能对流体的行为得到充分理解。
干水理论的另一不正确之处在于,在考虑流体与固体表面之间边界处的流动时我们所做的那种假设。过去当讨论经过柱体的流动——例如在图40-11中的那种流动——时,我们曾容许流体能沿固体表面滑动。在我们的理论中,在固体表面处的速度可以有任何值,这取决于该流动是怎样开始的,而我们就从未考虑过流体与固体之间的任何“摩擦”。然而,实验事实是,实际流体的速度在一固态物体的表面总是趋于零的。因此,我们关于柱体的解,不管有无环流,都是错误的——正如有关产生涡度的那种结果一样。我们将在下一章中告诉你们较为正确的理论。