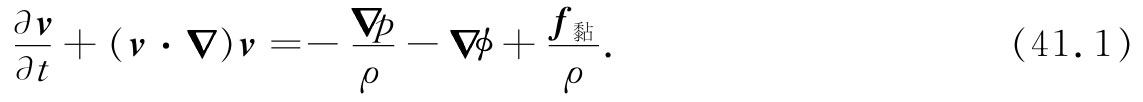
在上一章我们曾在忽略黏性现象的情况下讨论过水的行为，现在想要讨论包括 黏性效应在内的流体流动。我们希望考察流体的实际行为 ，定性地讨论在各种不同场合下流体的实际行为，使得你对这一课题将会有某些感触。虽然你将看到某些复杂方程，并听到某些复杂的事情，但这并非我们要求你必须学习所有这些东西的目的。在某种意义上，这是一章“文化课”，它将给予你这个世界存在方式的某些概念，其中只有一项是值得学习的，那就是我们立即将加以讨论的有关黏性的简单定义，其余的就只是为了向你们提供乐趣。
上一章中我们曾经发现，流体运动的规律全都包含在下述方程中，
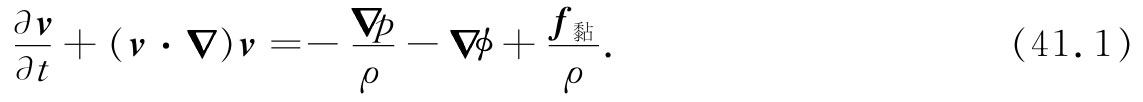
在我们的“干”水近似中曾去掉了末项，从而忽略了所有的黏性效应。并且，有时还由于考虑到流体是不可压缩的而做出一个附加近似，这时我们就有过一个补充方程
▽·v=0.
这最后一种近似往往很有效——特别是当流速比声速小得多的时候。但在实际流体中，认为可以略去我们所称之为黏性的那种内摩擦力几乎是绝对不正确的，而发生的大部分有趣的事情总是来自这种黏性。例如，我们曾见到在“干”水中环流永不会改变——如果开始时没有一个环流，往后也永不会有。可是，流体内的环流却是每天都要发生的事情。我们必须修补我们的理论。
我们从一个重要的实验事实着手。当我们过去算出“干”水环绕或经过一根柱体而流动——即所谓“有势流动”——时，我们没有理由不容许水具有与表面相切的速度，只有法向分量才必须等于零。我们并未把液体与固体之间或许会存在剪切力的那种可能性考虑进去。结果是——虽然并不是完全不言而喻的——在为实验所证实的一切场合下，在固体表面流体速度恰好为零 。无疑，你已注意到风扇叶片会积聚一薄层灰尘——而当风扇已经把空气搅动后灰尘仍然留在那里。甚至在风洞中的大型风扇上，你也可以看到同样的效应。为什么灰尘不会给空气吹跑了呢？虽然事实是扇叶正以高速穿越空气而运动，但空气相对于扇叶的速率在叶面上恰好趋向于零。因此，那些最小的尘埃粒子才没有被扰动 [1] 。所以我们必须对理论作出修正，以便能够与这个实验事实相符，即在一切通常的流体中，那些靠近固体表面的分子都会有零速度（相对于表面而言） [2] 。
我们原来是由这个事实来标志液体的，即如果你对它作用一个切应力——不管多么小——它就会放弃抵抗。它流动了。在静止情况下，不会有剪切应力。但在达到平衡之前——只要你仍然推动它——就可能存在剪切力。黏性 描述了存在于运动流体中的剪切力。为要得到流体运动时剪切力的量度，我们考虑下述实验。假设有两块其间夹有水的固体平面，如图41-1所示，保持其中一块固定，而另一块则以低速率v0 对其作平行运动。如果你对保持上板运动所需要的力进行测量，你会发现这力与板的面积和v0 /d都成正比，其中d为两板间的距离。因此，剪切应力F/A正比于v0 /d：
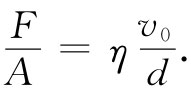
比例常数η称为黏性系数 。
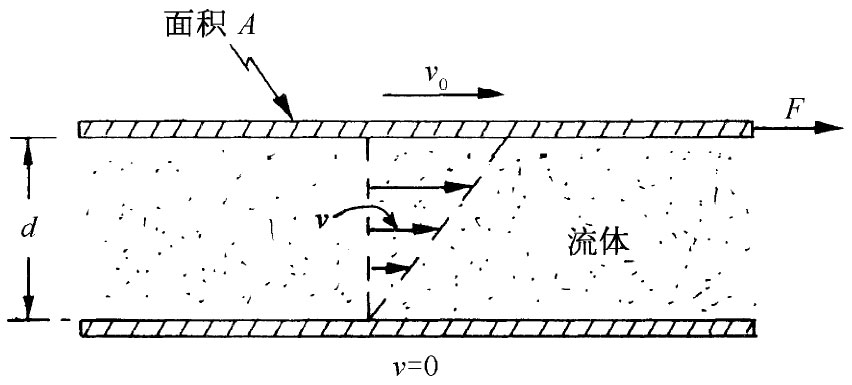
图41-1 在两平行板之间的黏性阻力
如果我们有一较复杂情况，则总可以考虑水中一个小而平坦的矩形单元，其上下两面都平行于水流，如图41-2所示。整个这单元上的剪切力由下式给出：
此时，∂vx /∂y就是我们曾在第38章中定义过的剪切应变的变化率 ，因而对于液体来说，剪切应力与剪切应变的变化率 成正比。
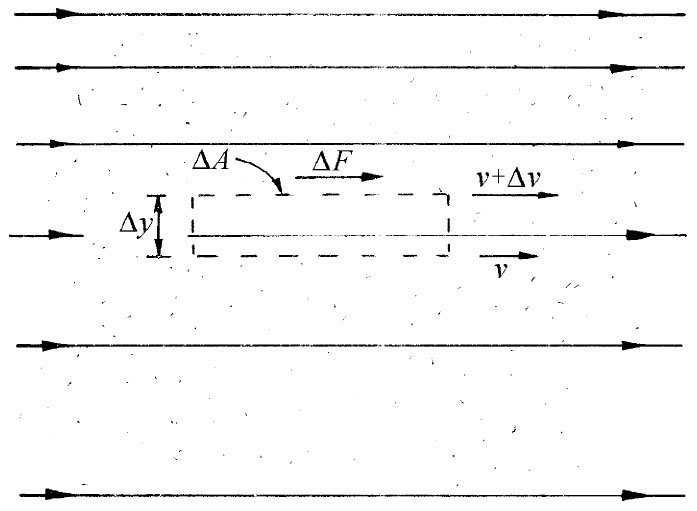
图41-2 在一黏性流体中的剪切应力
在一般情况下，我们写成
如果流体有一匀速转动，则∂vx /∂y是∂vy /∂x的负值，因而Sxy 为零——正应该如此，因为在匀速转动的流体中不存在应力（我们在第39章中对exy 下定义时做过类似的事情）。当然，还有关于Syz 和Szx 的相应表示式。
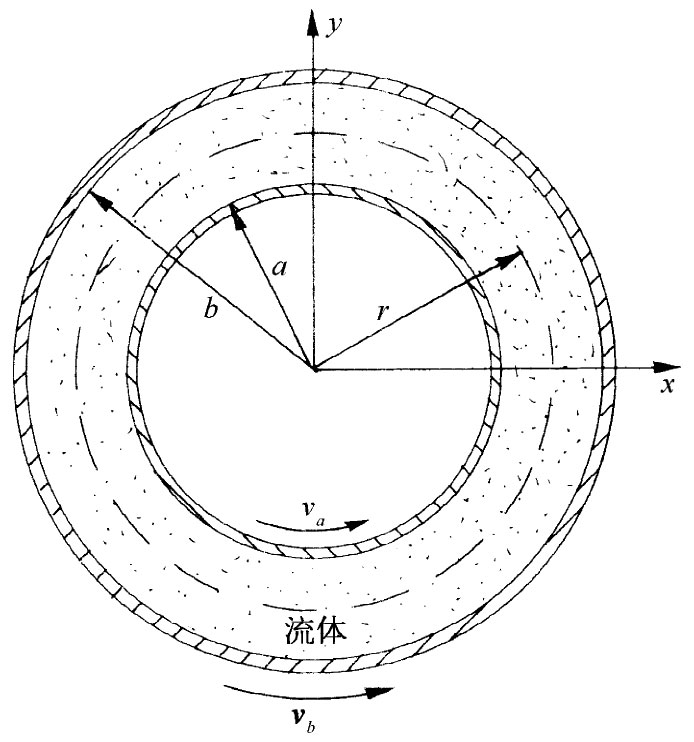
图41-3 在以不同角速度旋转着的两个同心筒之间流体的流动
作为应用这些概念的一个例子，我们考虑在两个同轴圆筒间流体的运动。设内筒半径为a，圆周线速度为va ，而令外筒具有半径b和圆周线速度vb ，参见图41-3。我们也许会问，在两筒之间的速度分布如何？为回答这一问题，我们从找出流体中距轴心为r处的黏性剪切力公式开始。根据问题的对称性，我们可以假定流动总是沿着切向的，而其大小仅取决于r，v=v（r）。如果注视水里半径为r处的一个小斑点，它的坐标作为时间的函数为
x=rcosωt，y=rsinωt，
其中ω=v/r。于是速度的x和y分量就是
vx =-rωsinωt=-ωy
和
vy =rωcosωt=ωx. （41.4）
根据式（41.3），我们有
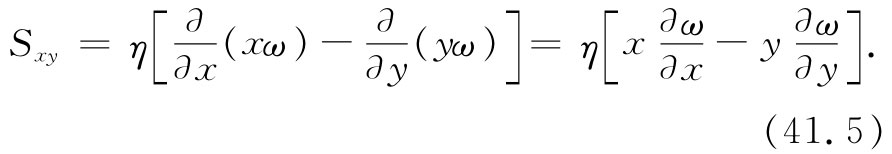
对于y=0的一点，∂ω/∂y=0，而x∂ω/∂x与rdω/dr相同。因此在该点上，
（S应依赖于∂ω/∂r是合理的，当ω不随r变化时，流体就处匀速转动之中因而不会有应力存在）。
我们已算出来的应力是切线方向剪切应力，围绕着整个柱面它们都相同。通过把剪切应力乘以矩臂r和面积2πrl，就可以获得作用于半径r处的整个柱形面 上的转矩 。我们得到
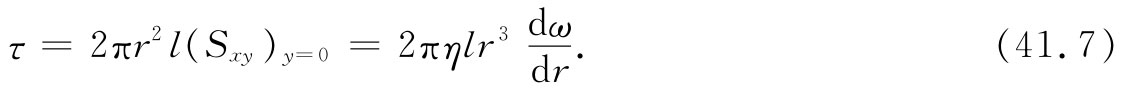
由于水的运动是定常的——没有角加速度——因而作用于r与r+dr间水的柱壳上净转矩必然为零，这就是说，在r处的转矩势必被在r+dr处的一个相等而相反的转矩所抵消，使得τ必须与r无关。换句话说，r3 dω/dr等于某个恒量，比方说A，因而
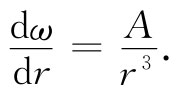（41.8）
积分后，我们求出ω随r的变化关系为：
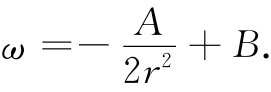（41.9）
A和B两常数，它们由满足在r=a处ω=ωa 和在r=b处ω=ωb 的条件而被确定下来。结果得到
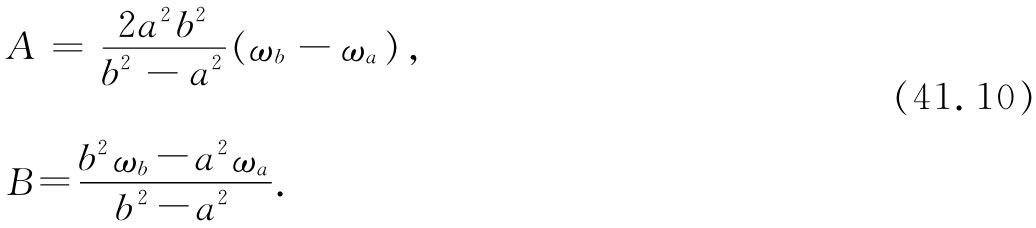
所以我们就知道作为r的函数的ω，从而也知道v=ωr。
如果希望得到转矩，则可由（41.7）和（41.8）两式得到：
τ=2πηlA
或
它与两筒的相对角速度成正比。测量黏性系数用的一种标准仪器就是这样制成的。其中一个圆筒——比方说外筒——安装在一个支枢上，但由测量作用于筒上转矩的弹簧秤来保持其稳定，而内筒则以恒定角速度旋转着。于是，黏性系数由式（41.11）确定。
根据η的定义，你可以看出它的单位是Nsm-2 。对于20℃的水来说，
η=10-3 Nsm-2 .
通常更方便的是采用比黏性 ，即η除以ρ，此时水与空气之值就可以进行比较：
在20℃的水， η/ρ=10-6 m2 s-1 ；
在20℃的空气， η/ρ=15×10-6 m2 s-1 . （41.12）
黏性通常强烈地依赖于温度。例如，对于刚好在凝固点时的水，其η/ρ比在20℃时的要大1.8倍。