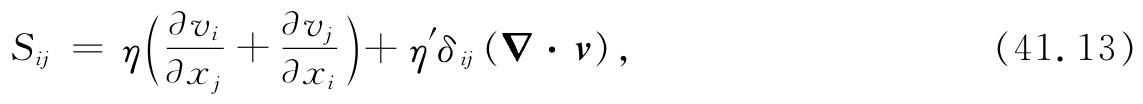
现在我们研究黏性流动的最普遍理论——至少是人类已经知道的最普遍形式。我们已经了解到剪切应力分量与各种速度分量的空间微商(诸如∂vx /∂y或∂vy /∂x)成正比。然而,在可压缩 流体的普遍情况下,应力中还存在取决于速度其他微商的另外的项。普遍的表示式为
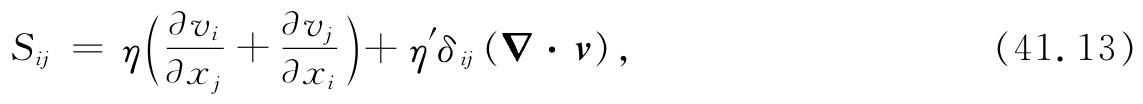
式中xi 是直角坐标x,y或z中的任一个,而vi 则是速度的直角坐标中的任一个(δij 是克罗内克符号,当i=j时为1,而当i≠j时为零)。该附加项对于应力张量的所有对角元Sii 都增添了η′▽·v。如果流体是不可压缩的,则▽·v=0,而这一附加项就不见了。所以它与受压缩时的内力有关。因此要描述流体就需要两个常数,正如我们过去在描述均匀弹性固体时曾有过两个常数一样。系数η即我们曾遇到的“普通”黏性系数。它也被称为第一黏性系数 或“剪切黏性系数”,而新的系数η′被称为第二黏性系数 。
现在要确定单位体积里的黏性力f黏 ,以便能将其代入式(41.1)中而获得实际流体的运动方程。作用于流体中一小立方体上的力,等于作用在所有六个面上之力的合力。每次取其中两个面,将获得其差值,该值决定于应力的微商、亦即速度的二次微商。这很好,因为将会使我们回到矢量方程式上来。每单位体积的黏性力在直角坐标xi 方向的分量为
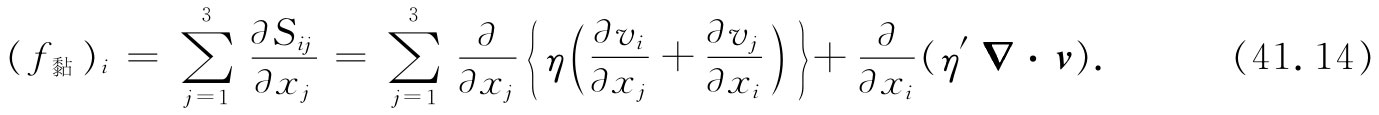
通常,黏性系数随位置的变化并不重要,因而可以忽略,这样,单位体积的黏性力就仅含有速度的二次微商。在第39章中,我们看到在一个矢量方程中可能存在的二次微商的最普遍形式为,含拉普拉斯符号(▽·▽v=▽2 v)的项与含散度的梯度项(▽(▽·v))两者之和。式(41.14)恰好就是具有系数η和(η+η′)的这样一个和。我们得到
f黏 =η▽2 v+(η+η′)▽(▽·v). (41.15)
在不可压缩的情况下,▽·v=0,因而单位体积的黏性力正好是η▽2 v。那就是许多人所用到的全部内容。然而,如果你要计算流体中声波的吸收,那你就会需要第二项了。
现在可以完成实际流体运动的普遍方程方面的工作了。把式(41.15)代入(41.1)中,得
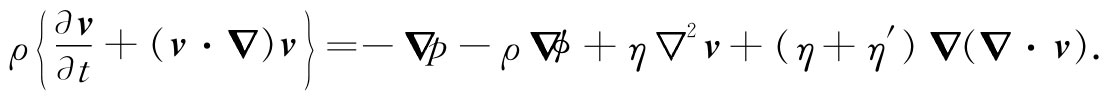
它是一个复杂的方程,但大自然就是这个样子。
如果像以往一样引进涡度Ω=▽×v,那么就可将上述方程写成
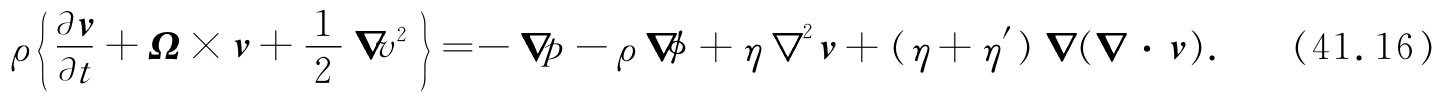
我们再次假定唯一起作用的彻体力是像重力那样的保守力。为弄清楚新项意味着什么,让我们考察不可压缩流体的情况。于是,如果取式(41.16)的旋度,则得到
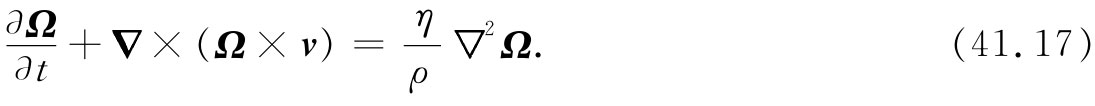
这个式子除了在其右边有一新项外就很像式(40.9)了。当右边为零时,我们曾有过涡度随流体一起运动的亥姆霍兹定理。现在,虽然在右边已有相当复杂的非零项,然而,它却具有简单明了的物理意义。如果暂时略去项▽×(Ω×v),则得到一个扩散方程 。该新项意味着涡度Ω经由流体而扩散 。如果在涡度方面存在一个大的梯度,则它将会扩散到其邻近的流体中去。
这就是引起烟环在前进时会变得较厚的那一项。同样,如果你把一个“洁净”的涡环(由上一章所描述的那台仪器造成的“无烟”环)送过烟雾,则它就可以漂亮地被显示出来。当它跑出烟雾时,它已很好地吸取了某些烟雾,所以你会看到一个空心的烟环壳。有些Ω向外扩散进烟雾之中,但仍能保持与涡旋一起向前运动。