现在来讨论主要问题。它是真的吗?我们生活的现实的物理三维空间是弯曲的吗?一旦我们具有了足够的想象力去认识空间是不是被弯曲了的可能性,那么人类的脑子自然就对现实世界是否弯曲变得好奇起来。为了尝试得出解答,人们已经进行了直接的几何测量,但没有发现任何差异。但从另一方面来说,根据有关引力的论证,爱因斯坦发现空间是弯曲的,而我们想要告诉你们关于曲率大小的爱因斯坦定律是什么,也希望对你们讲一点关于他是如何发现这个定律的情况。
爱因斯坦曾说,空间是弯曲的,而物质是曲率之源(物质也是引力之源,所以重力与曲率有关——但这种关系将在本章的后期涉及)。为了使事情稍微容易些,我们假定物质以某种密度连续地分布,然而,密度可以按你想要的大小逐处变化 [4] 。对于曲率,爱因斯坦给出的规则如下:如果有一个空间区域内部存有物质,而我们取一个足够小的球,其内部的物质密度ρ实际上为常数,那么该球半径的逾 正比球内的质量。利用逾半径的定义,得
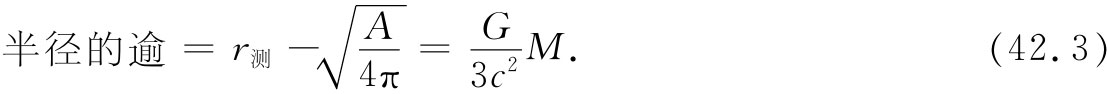
式中G为(牛顿理论的)引力常数,c为光速,M=4πρr3 /3是球内物质的质量。这就是空间平均曲率的爱因斯坦定律。
假定以地球为例,且不考虑密度的逐点变化——所以不必做任何积分。假定我们非常仔细地测量地球的表面,然后挖一个洞通到中心并测得其半径。根据球的面积等于4πr2 的假设,由所测面积可以计算出预期半径。当把预期半径与实际半径进行比较时,会发现实际半径超过预期半径,其值由式(42.3)给出。常数G/(3c2 )约为2.5×10-29 cmg-1 ,所以对每一克物质来说,其测量半径就要多出2.5×10-29 cm。代入约为6×1027 g的地球质量,结果是地球具有的半径比根据其面积计算应得的半径大1.5mm [5] 。对太阳做相同的计算,你会发现太阳的半径比预期值超出半公里。
你会注意到该定律说,地球表面区域的上方平均 曲率为零。但这并不 意味着曲率的所有分量为零。地球上方可能仍然存在——而事实上是存在——某种曲率。就平面上的一个圆来说,对于某些取向将有一种符号的逾半径,而对于另外一些取向则逾半径的符号相反。结果正好证明当球内 的质量为零时曲率对整个球面的平均为零。顺便说说,结果表明曲率的各个分量与平均曲率的逐处变化 之间存在着联系。所以如果你知道了各处的平均曲率,你就能计算出每个地方曲率分量的细节。地球内部的平均曲率是随深度变化的,这就意味着地球内部和外部的某些曲率分量都不为零。正是这种曲率,我们把它看作为引力。
假定在平面上有一只昆虫,而且假定这个“平面”的表面有些小突起。凡是有小突起的地方,昆虫会得出结论说:它的空间具有小的局部弯曲的区域。在三维中也有同样的情况,凡是物质堆积的地方,三维空间就有局部弯曲——一种三维突起。
如果在平面上造成许多隆起,则除了所有的突起以外,可能存在总体的弯曲——表面或许变得像一个球。搞清楚我们的空间是否由于像地球和太阳那样的物质堆积而形成局部的突起,从而具有净的平均曲率,这应该是有意义的。天体物理学家一直试图通过对非常遥远的星系的测量来回答这个问题。例如,若我们在很远距离处的球壳内所观测到的星系数目,与根据我们所知的球壳半径应该预期到的数目不同,则我们就会得到关于非常大的球的逾半径的量度。根据这种测量,希望找出我们的整个宇宙就平均而言究竟是平坦的,抑或是球形的——是像一个球那样是“闭合”的,还是像一个平面那样是“开放”的。你们可能听说过有关这个问题的争论,这个争论还将继续下去。争论所以会存在,是因为天文学测量仍然完全没有确定的结果;实验数据又不够精确,不能给出确切的答案。可惜,我们在大尺度方面还没有关于宇宙整体曲率的丝毫概念。