§42-7　时空的曲率

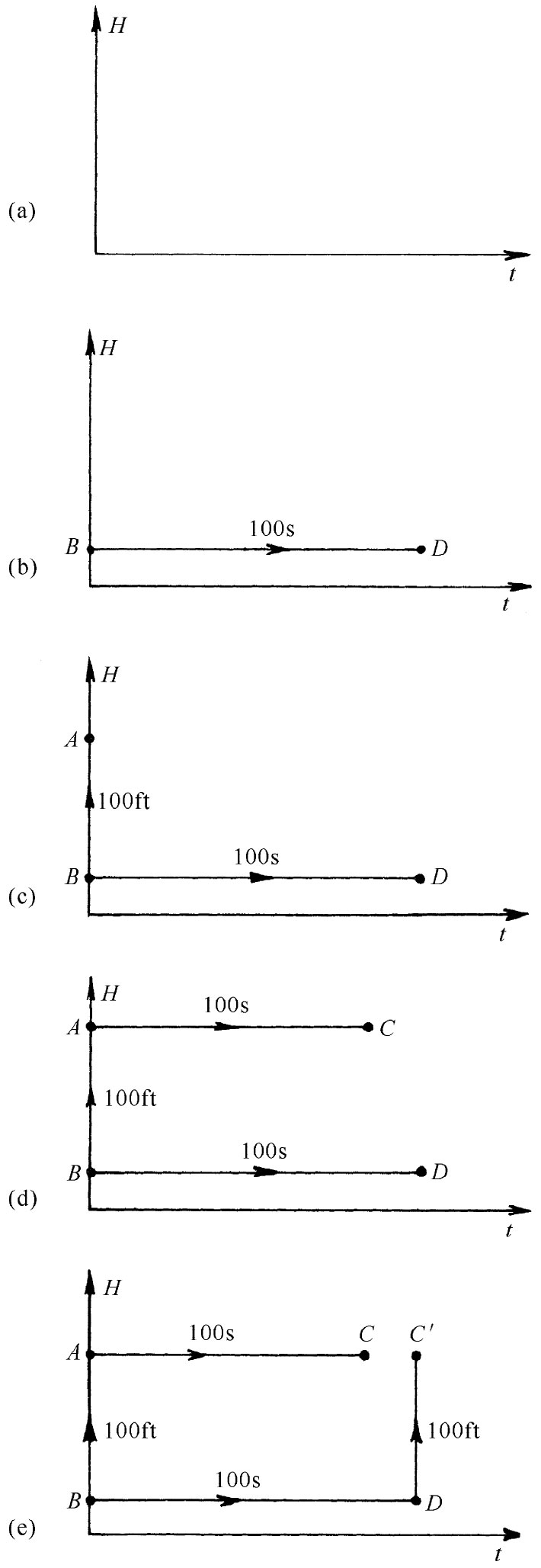
现在我们要把刚才所讲的情况与弯曲的时空概念联系起来。已经指出，如果时间在不同的地方以不同的快慢进行，则这种情况就与热板的弯曲空间相类似。但它不只是类似，还意味着时空是弯曲的。让我们尝试在时空中做某种几何图形。这种事初听起来可能觉得奇怪，但我们经常用沿一根轴表示距离及沿另一根轴表示时间做时空图。假定我们尝试在时空图中做一个矩形。我们先画一个高H与t的关系图，如图42-18（c）所示。为了做矩形的底边，可以取一个静止 在高H1 处的物体，并跟着它的世界线走100s，就得到图（b）中的BD线，它平行于t轴。现在选取另一个物体，在t=0的时刻它位于第一个物体上面100ft处，它从图42-18（c）中的A点出发，现在沿着它的世界线前行100s，这由位于A点的钟测得。物体从A运动到C，如图中（d）所示。但注意，由于时间在两个高度——假定存在引力场——以不同的快慢进行——所以C和D两点不是同时的。如果试图通过画一条线到达处于相同时刻、位于D上面100ft的点C′而完成一个矩形，如图42-18（e）所示，则几条线无法闭合。当我们说时空是弯曲的时候，就是这个意思。

图42-18　尝试在时空图中做一个矩形