§42-8 在弯曲时空中的运动
我们来考虑一个有趣的小谜。有两只相同的钟A和B,如图42-19所示,一起放在地球的表面上。现在把钟A举到某个高度H,在那里待一会儿,再返回地面,使它刚好在钟B走了100s时到达地面。这样钟A会读出像107s这种数目,这是由于它在空中上升时走得较快。此时就产生了一个谜。我们应该如何移动钟A才能使得它读出尽可能长的时间——始终假定它返回时B钟读数为100s?你说:“这容易。只要你把A举得尽可能高,那么它将走得尽可能的快,因而在返回时读出的时间最长。”错!你忘记了一件事——我们只有100s供上升和返回。要是我们升得很高,则我们就得很快到达那儿以便在100s内返回。你务必不能忘了狭义相对论的效应,它会导致运动的钟减慢
一个因子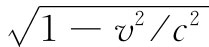 。相对论效应在这方面起的作用使钟A的读出时间
比钟B的小
。你们看看这类游戏。如果我们带着钟A一直站着,就能得到100s读数;要是我们缓慢上升一个很小的高度并缓缓下降,则就能得到稍微大于100s的读数。如果我们升得稍高一些,得到的时间读数可能稍长一些。但要是升得太高,则为到达那儿就必须运动得很快,这就必须使钟下降得足够慢,以至使结束时得到的时间少于100s。该用什么样的高度与时间关系程序——达到多高及以什么速率到达那儿、如何仔细调节使得我们回到钟B时它的读数增加了100s——才会使钟A给我们读出尽可能最长的时间?
。相对论效应在这方面起的作用使钟A的读出时间
比钟B的小
。你们看看这类游戏。如果我们带着钟A一直站着,就能得到100s读数;要是我们缓慢上升一个很小的高度并缓缓下降,则就能得到稍微大于100s的读数。如果我们升得稍高一些,得到的时间读数可能稍长一些。但要是升得太高,则为到达那儿就必须运动得很快,这就必须使钟下降得足够慢,以至使结束时得到的时间少于100s。该用什么样的高度与时间关系程序——达到多高及以什么速率到达那儿、如何仔细调节使得我们回到钟B时它的读数增加了100s——才会使钟A给我们读出尽可能最长的时间?
试回答:求出你必须用多大的速率把一个球向上抛入空中,使得它正好在100s内落回至地球。而该球的运动——快速上升、慢下来、停止再返回——这正是使得固定于球上的手表的时间为最大的、正确的运动。
现在考虑稍微不同的游戏。设A和B两点同在地球表面且相隔某段距离。我们玩一个与早先做过的相同游戏,即求所谓的直线。试问应该如何从A移动到B,才能使得运动手表上的时间最长——假定我们一得到给定信号就从A点出发,而在B一有另一个信号时就到达B点——该后一信号按固定钟比前一信号迟100s。现在你们会说:“唔,我们前已求出,要做的事情就是以适当的均匀速率沿直线滑行,使得恰好在100s后到达B点。如果我们不沿直线运动,则要用更大的速率,这样我们的表就会慢下来。”但是等一下,那是以前考虑重力的情况。向上弯曲一点然后下降不是更好吗?这样,在升得较高的时间阶段中我们的表不是会跑得稍快一点吗?情况确是这样。如果你们求解调节运动曲线的数学问题,使得运动手表经过的时间尽可能长,则你将发现运动轨迹是一条抛物线——就是引力场中沿自由弹道路径运动的物体所遵循的同一条曲线,如图42-19所示。所以引力场中的运动定律也可表述为:一个物体从一个地方运动到另一个地方,它总是使得其所携带的钟给出的时间比之在其他任何可能的轨道上运动所用的时间要长——当然,开始和结束的条件应相同
。运动的钟测得的时间常常称为“固有时”。在自由落体运动中,运动轨道使得物体的固有时最大。
图42-19 在均匀引力场中,对于固定的飞行时间来说,固有时最长的轨迹是抛物线
我们来看看这一切是如何算出来的。从式(42.5)开始,它说明运动手表的逾
速率为
 (42.13)
(42.13)
除此之外,我们得记住,对速率来说还存在相反符号的修正。关于这个效应,已知
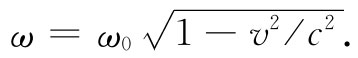
虽然该原理对任何速率都适用,但在我们所举的例子中速率总要比c小得多,因此可以把这个方程写成
ω=ω0
[1-v2
/(2c2
)],
而以我们的钟的速率来看,亏损为
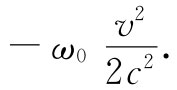 (42.14)
(42.14)
把式(42.13)和(42.14)中的两项结合起来,得
运动钟的这种频移意味着:如果在固定的钟上测得时间dt,则运动钟所记录的时间为
整个轨道的总的时间逾为附加项对时间的积分,即
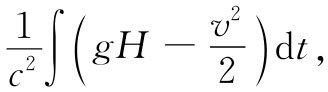 (42.17)
(42.17)
它应为极大。
项gH正好就是引力势ϕ。假定用常数因子-mc2
乘以整个式子,这里m为物体的质量,这个常数虽不改变极大的条件,但负号将把极大正好改变为极小。于是式(42.16)指出,物体的运动将使得
但现在的被积函数正好是动能和势能的差。如果你们顺便看一下第2卷第19章,就会知道在我们讨论最小作用量原理时就已证明,对于任何势场中的一个物体来说,牛顿定律正好可以写成方程式(42.18)的形式。
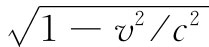 。相对论效应在这方面起的作用使钟A的读出时间
比钟B的小
。你们看看这类游戏。如果我们带着钟A一直站着,就能得到100s读数;要是我们缓慢上升一个很小的高度并缓缓下降,则就能得到稍微大于100s的读数。如果我们升得稍高一些,得到的时间读数可能稍长一些。但要是升得太高,则为到达那儿就必须运动得很快,这就必须使钟下降得足够慢,以至使结束时得到的时间少于100s。该用什么样的高度与时间关系程序——达到多高及以什么速率到达那儿、如何仔细调节使得我们回到钟B时它的读数增加了100s——才会使钟A给我们读出尽可能最长的时间?
。相对论效应在这方面起的作用使钟A的读出时间
比钟B的小
。你们看看这类游戏。如果我们带着钟A一直站着,就能得到100s读数;要是我们缓慢上升一个很小的高度并缓缓下降,则就能得到稍微大于100s的读数。如果我们升得稍高一些,得到的时间读数可能稍长一些。但要是升得太高,则为到达那儿就必须运动得很快,这就必须使钟下降得足够慢,以至使结束时得到的时间少于100s。该用什么样的高度与时间关系程序——达到多高及以什么速率到达那儿、如何仔细调节使得我们回到钟B时它的读数增加了100s——才会使钟A给我们读出尽可能最长的时间?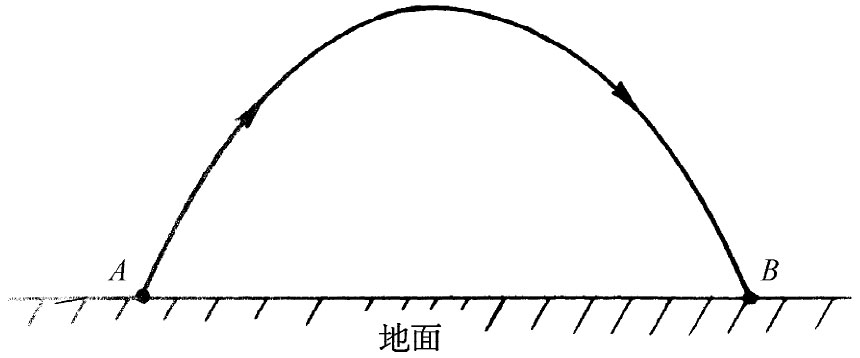
 (42.13)
(42.13)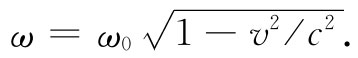
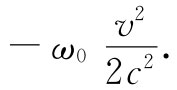 (42.14)
(42.14)

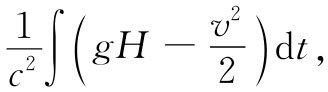 (42.17)
(42.17)