第20章 空间转动
§20-1 三维空间中的转矩
在本章中我们将讨论转轮的行为,这是力学中最引人注目和最有趣的成果之一。为此,我们必须首先把转动的数学公式、角动量原理、转矩等概念推广到三维空间中去。我们不准备使用 这些公式的最一般的形式,也不准备研究它们的全部结果,因为这可能要花几年的时间,而我们必须很快转向讨论其他课题。在一门导论课程中,我们只能介绍一些基本定律,并把它们应用到少数几个特别有趣的情况中。
首先,我们注意到,对于在三维空间中的转动,无论转动体是刚体或其他任何系统,在二维空间中导出的定理仍然是正确的。也就是说,xF y -yF x 仍是在“xy 平面”的转矩,或“相对于z 轴”的转矩。而且这个转矩也仍然等于xp y -yp x 的变化率,因为假如重温一下从牛顿定律推导式(18.15)的过程,我们就可以看到毋须假设运动是在平面内进行的;当我们对xp y -yp x 微分时,就得到xF y -yF x ,所以,这个定理仍然是正确的。于是,量xp y -yp x 称为属于xy 平面的角动量,或相对于z 轴的角动量。这一点既然成立,我们可以采用其他任何一对轴,并得出另一个公式。例如,我们可以采用yz 平面,很明显,根据对称性,只要用y 代替x ,用z 代替y ,我们就可以找到转矩yF z -zF y ,以及与yz 平面相联系的角动量yp z -zp y 。当然,我们还可以采用zx 平面,对这个平面,将有zF x -xF z =d(zp x -xp z )/dt 。
十分清楚,对于单个粒子的运动可以推导出这三个公式。而且,假如把许多粒子的诸如xp y -yp x 这样的量加在一起,并称之为总角动量,那么对于xy ,yz ,zx 的三个平面,我们可以得到三类表示式。用同样的办法处理力,我们也可以得到在xy ,yz ,zx 平面的转矩。因此,可以得出这样的定律,即与任一平面相联系的外转矩等于与此平面相联系的角动量的变化率。这正是二维空间中我们曾经写出的表示式的推广。
但是,也许有人会说:“噢,不过平面不只三个,还有许多平面,难道我们不能在某一角度上取某一平面,并由力来计算出在这个平面上的转矩吗?对于每一个这样的平面,我们都可以写出一组不同的方程式,这样,我们将有多少方程式啊!”十分有趣的是,结果表明,假如我们对另一个平面测出x
′,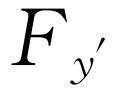 等等,从而得出关于该平面的表示式
等等,从而得出关于该平面的表示式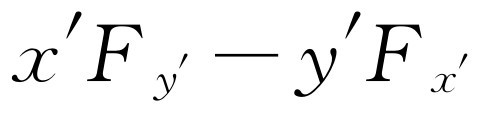 ,那么结果可以写成对于xy
,yz
,zx
三个平面的三个表示式的某种组
合。这里毫无新的东西。换句话说,假如我们知道在xy
,yz
,zx
平面内的三个转矩,则在任何其他平面上的转矩和相应的角动量总可以写成这三个转矩的某种组合:比如其中一个的6%加另一个的92%,等等。现在,我们将要分析这个性质。
,那么结果可以写成对于xy
,yz
,zx
三个平面的三个表示式的某种组
合。这里毫无新的东西。换句话说,假如我们知道在xy
,yz
,zx
平面内的三个转矩,则在任何其他平面上的转矩和相应的角动量总可以写成这三个转矩的某种组合:比如其中一个的6%加另一个的92%,等等。现在,我们将要分析这个性质。
假如,在xyz
这组轴中,乔得出了他的三个平面的所有转矩和角动量,但莫具有在另一方向的轴x
′,y
′,z′
。为了使问题简单一些,我们将假定只是x
和y
轴转了一个角度。莫的x
′和y
′是新的,但是他的z′
正好和z
相同。这就是说他具有新的yz
和zx
平面。因此,他得求出新的转矩和角动量。例如,在x
′y′
平面内,他的转矩应该是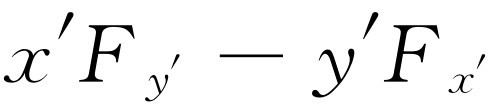 ,等等。现在,我们要做的是求出新转矩和旧转矩之间的关系,从而使我们能够建立从一组坐标轴到另一组坐标轴之间的联系。可能又有人会说:“这看起来正和处理矢量的问题一样。”确实如此,我们就是要那样做。然后他可能还会问:“那么,转矩不正是一个矢量吗?”结果表明,它是一个矢量,但是如果不加分析,我们就不能立即明白这一点。因此,下面来作分析。我们将不打算详细地讨论每一步骤,因为我们只需要说明如何处理问题。乔算出的转矩为
,等等。现在,我们要做的是求出新转矩和旧转矩之间的关系,从而使我们能够建立从一组坐标轴到另一组坐标轴之间的联系。可能又有人会说:“这看起来正和处理矢量的问题一样。”确实如此,我们就是要那样做。然后他可能还会问:“那么,转矩不正是一个矢量吗?”结果表明,它是一个矢量,但是如果不加分析,我们就不能立即明白这一点。因此,下面来作分析。我们将不打算详细地讨论每一步骤,因为我们只需要说明如何处理问题。乔算出的转矩为
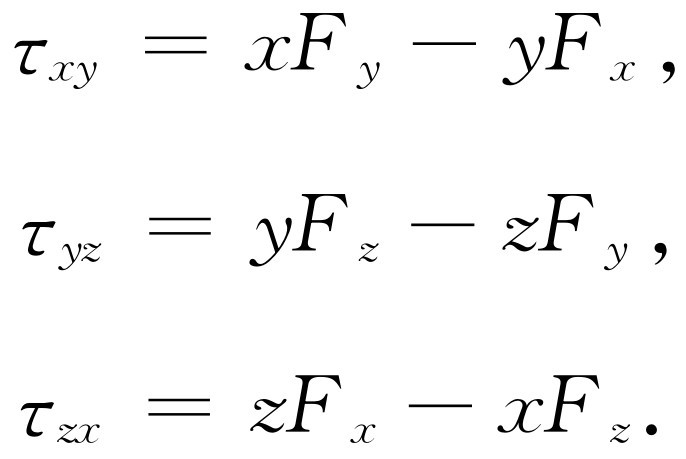 (20.1)
(20.1)
这里我们离题插一句,请注意,在类似于这样的情况下,如果坐标处理不当,人们可能会把某些量的符号搞错。为什么不写成τ yz =zF y -yF z ?问题在于:一个坐标系既可以是“右旋的”,也可以是“左旋的”。一旦对它们(任意地)选定一种符号,如τ xy ,则其他两个量的正确表达式总可以根据下面任何一种次序中xyz 字母的互换而求出

莫在他的坐标系中算出的转矩为
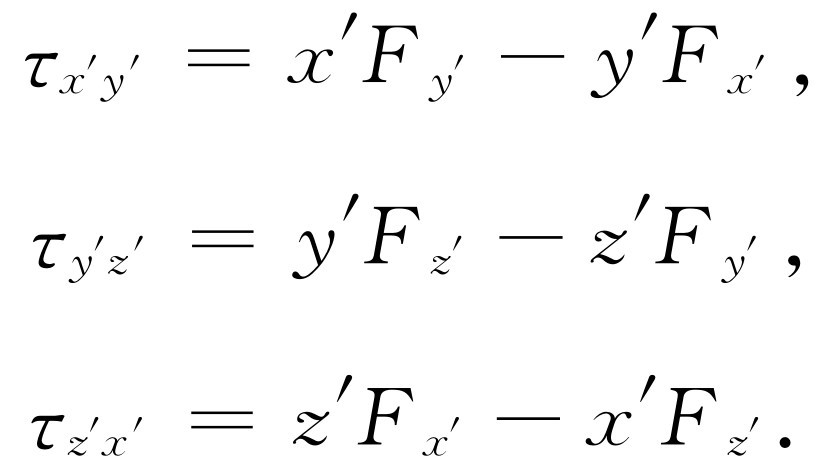 (20.2)
(20.2)
现在假设某一个坐标系转过了一个固定角度θ ,从而使得z 和z ′相同(这个角度θ 与物体的转动无关,也与坐标系内发生什么情况无关。它仅仅是一个人所采用的坐标轴与另一个人采用的坐标轴之间的联系,我们假定它是常数)。因此,两个坐标系中的坐标之间的关系为
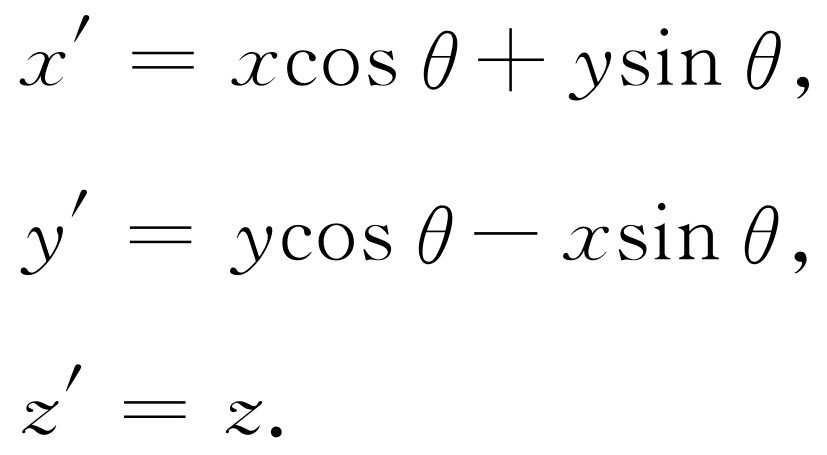 (20.3)
(20.3)
同样,因为力是矢量,所以它以与x ,y ,z 相同的方式变换到新的坐标系,这是由于当且仅当一个量的各个分量以与x ,y ,z 同样的方式变换时,才是矢量
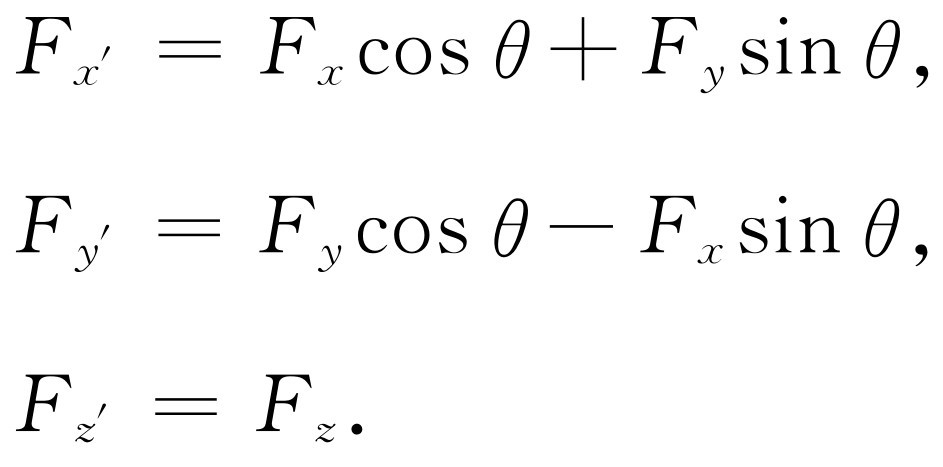 (20.4)
(20.4)
现在,只要把式(20.3)的x
′,y
′和z
′与式(20.4)的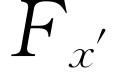 ,
,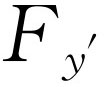 和
和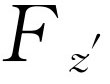 统统代入式(20.2),我们就能求出转矩的变换。这样,我们就得出
统统代入式(20.2),我们就能求出转矩的变换。这样,我们就得出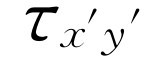 的包含有一长串项的表达式,而结果(乍一看来,颇觉惊讶)它正好简化成xF
y
-yF
x
,这正是xy
平面内的转矩
的包含有一长串项的表达式,而结果(乍一看来,颇觉惊讶)它正好简化成xF
y
-yF
x
,这正是xy
平面内的转矩
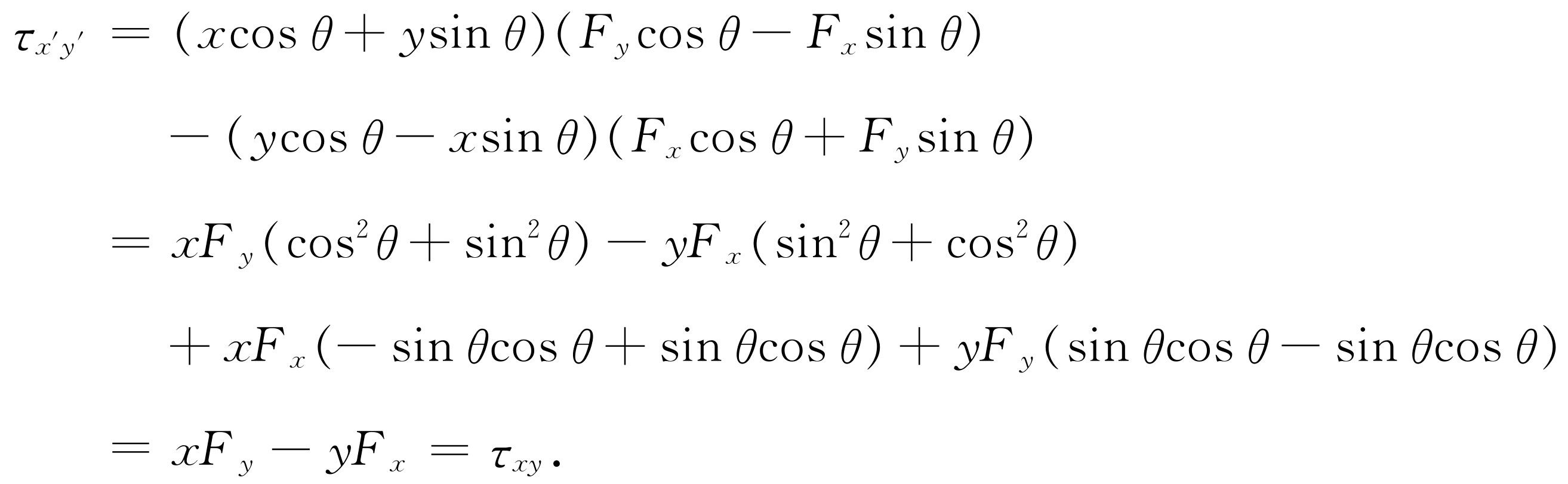 (20.5)
(20.5)
这个结果是很清楚的,因为假如我们仅在平面
上转动轴,则在那个平面内对z
轴的扭转与以前不会有什么不同,因为这是同一个平面!我们更感兴趣的是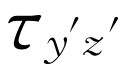 的表达式,因为这是一个新的平面。现在在y
′z
′平面来进行完全相同的变换,结果如下
的表达式,因为这是一个新的平面。现在在y
′z
′平面来进行完全相同的变换,结果如下
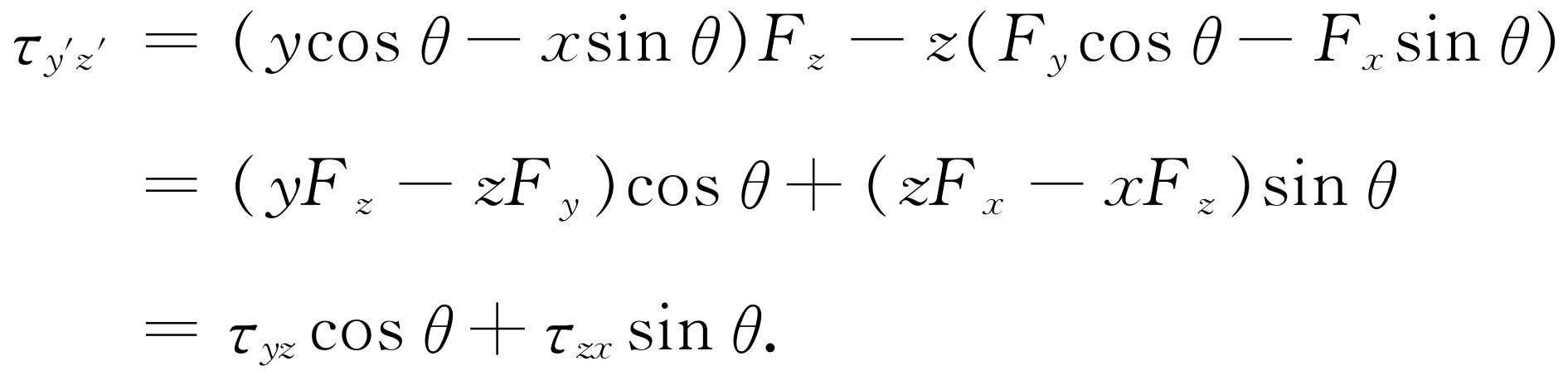 (20.6)
(20.6)
最后,对z ′x ′平面有
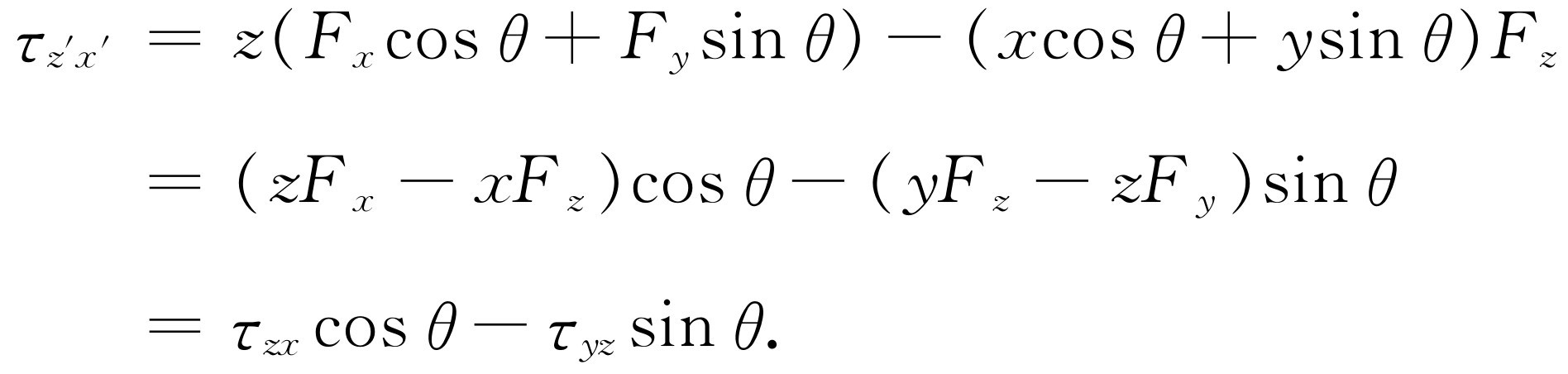 (20.7)
(20.7)
我们需要求出借助于旧坐标轴的转矩来表示新坐标轴转矩的规则,现在已经有了这条规则。我们怎样才能记住它呢?仔细观察一下式(20.5),(20.6)和(20.7),就可以看出这些等式与x ,y 和z 的等式之间有一个密切的关系。如果我们把τ xy 叫做某个量的 z 分量 ,例如称它为τ 的z 分量,那就好了,因为z 分量应该不变,而式(20.5)正是如此,所以可以把式(20.5)理解为一个矢量变换。同样,如果我们把新引入的矢量的x 分量和yz 平面联系起来;把y 分量和zx 平面联系起来,则这些变换的表示式可以写成
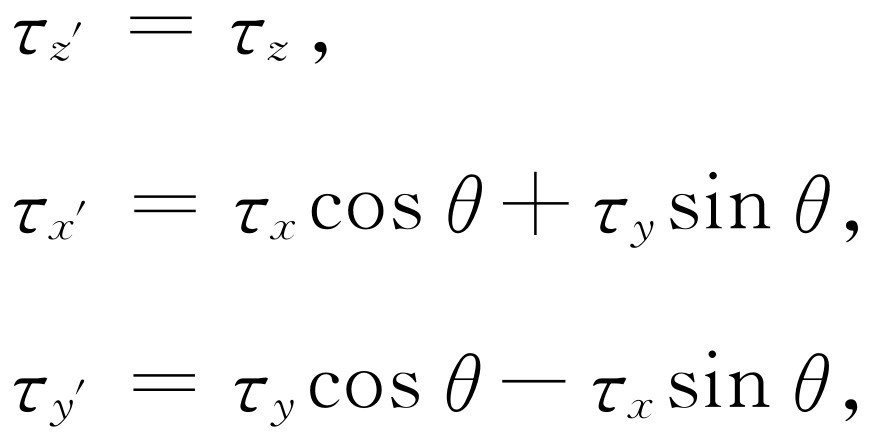 (20.8)
(20.8)
这正是矢量变换的法则!
因此,这就证明了我们可以把组合式xF y -yF x 与矢量的z 分量等同起来。虽然转矩是在一个平面上的扭转,并不具有先验的矢量特征,但在数学上它的确就像一个矢量。这个矢量垂直于扭转平面,它的大小与扭转强度成正比。这样一个量的三个分量就像真正的矢量一样变换。
因此,我们就用矢量来表示转矩;假设转矩作用在一个平面上,用尺画一条垂直于该平面的直线。但是仅仅说“垂直”于平面,还没有规定符号。为了正确确定符号,我们必须采用一个规则,使得利用这个规则,能够告诉我们假如转矩以某种方式作用在xy 平面上,那么与之相联系的轴是沿z 的正方向。也就是说,人们必须规定“左”和“右”。假设坐标系是右旋系统中的x ,y ,z ,那么这个法则可以描述如下:如果我们把扭转想象为旋转一个具有右旋螺纹的螺钉,那么与扭转有关的那个矢量的方向就是螺钉前进的方向。
为什么转矩是一个矢量呢?我们能够把一个平面和单一的一根轴联系起来,从而能把矢量和转矩联系起来是十分幸运的奇迹;这是三维空间的一个特性。在二维空间中,转矩是一个普通的标量,没有规定方向的必要。在三维空间中,它是一个矢量。假如是四维空间,困难就很大,因为(例如我们取时间为第四维)不仅有xy ,yz 和zx 平面,还有tx ,ty 和tz 平面。这里有6个 面,人们不能把6个量表示为四维空间中的一个矢量。
我们长期地生活在三维空间中,因此值得指出,前面的数学处理与x 代表位置,F 代表力这些事实无关,它只依赖于矢量的变换规律。因此,如果用某个其他矢量的x 分量来代替x,结果将毫无差别。换句话说,假如我们要计算a x b y -a y b x (这里 a 和 b 是矢量),并把它称为某一新的量c 的z 分量,那么这些新的量组成了矢量 c 。我们需要找出一个数学表达式来表示具有三个分量的这个新的矢量与矢量 a 和 b 之间的关系。为此而设想的表示方法是 c = a × b 。这样,除了在矢量分析理论中通常的标积之外,又有一种新的乘法,称为矢积 。因而假如 c = a × b ,就等于写成下面的形式
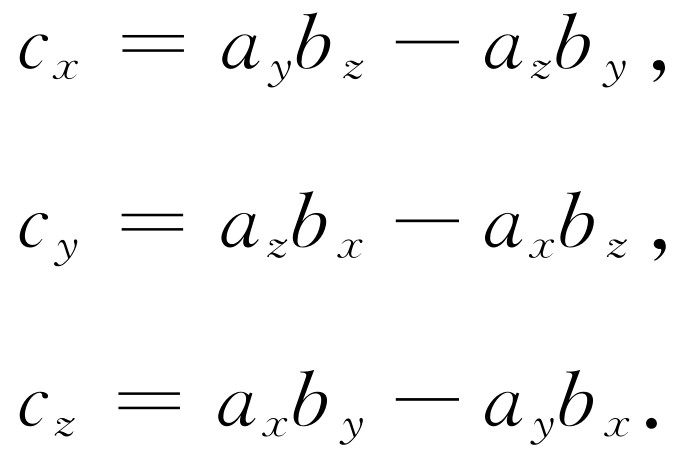 (20.9)
(20.9)
假如把 a 和 b 的次序颠倒一下,即把 a , b 改为 b , a ,则 c 的符号也必须颠倒一下,因为c z 应该是b x a y -b y a x 。因此,叉积与一般的乘法不一样,在一般的乘法中ab =ba ,而对叉积 b × a =- a × b 。由此我们立即可以证明,假如 a = b ,其叉积为零,即 a × a =0。
叉积对表达转动的特性十分重要,因此,掌握三个矢量 a , b , c 的几何关系是很重要的。当然,分量之间的关系已由式(20.9)给出,从那里也可以确定它们在几何上的关系。结果是首先矢量 c 同时垂直于 a 和 b (试计算 c · a ,看它是否为零)。其次, c 的大小可以证明等于 a 的大小乘 b 的大小再乘两者之间夹角的正弦。 c 指向什么方向呢?设想把 a 转过一个小于180°的角到 b ;用这样的方法转动一个右旋螺纹的螺钉,螺钉前进的方向就是 c 的方向。我们用右 旋螺钉而不用左 旋螺钉,这是一个习惯问题,而且它不断提醒我们,假如 a 和 b 是一般意义下的“真正的”矢量,那么由a ×b 创造的新的“矢量”是人为的,它的性质与 a 和 b 略有差别,因为它是由一个特殊法则构成的。假如 a 和 b 是所谓的普通矢量,我们给它们取一个专门的名称叫做极矢量 。例如坐标 r 、力 F 、动量 p 、速度 v 、电场 E 等等都是这种矢量,这些都是通常的极矢量。在它们的定义中只包含一次叉积的矢量叫做轴矢量或赝矢量 。转矩 τ 和角动量 L 当然就是赝矢量的例子。还可以发现角速度 ω 和磁场 B 也是赝矢量。
为了使矢量的数学性质完整,我们应该知道关于矢量的点积和叉积的所有规则。在目前的应用中,我们只需要知道很少一点就够了,但是为了完整起见,我们将写出所有矢量乘法的规则,便于今后应用。它们是
 (20.10)
(20.10)
§20-2 用叉积表示的转动方程式
现在我们要问,是否在物理学中的任何方程都可以写成叉积的形式呢?回答是大多数的方程都可以这样写。例如,我们立即可以看出转矩等于位置矢量和力的叉积
τ = r × F .(20.11)
这是包含τ x =yF z -zF y 等三个方程式的一个矢量。根据同样的想法,假如只有一个粒子时,角动量矢量就是离原点的距离乘以动量矢量
L = r × p .(20.12)
对于三维空间转动来说,与牛顿的 F =d p /dt 定律相类似的动力学定律是:转矩矢量等于角动量矢量随时间的变化率
τ =d L /dt .(20.13)
假如把式(20.13)对很多粒子求和,那么作用在一个系统上的外转矩是总角动量的变化率
τ 外 =d L 总 /dt .(20.14)
另一个定理是:若总的外转矩为零,则这个系统的总角动量矢量不变。这称为角动量守恒定律 。假如没有转矩作用在一个给定系统上,它的角动量就不会改变。
角速度情况如何呢?它是矢量吗?我们已经讨论过固体绕一个给定轴的转动,现在假定我们使它同时绕两 根轴转动。它可以一方面绕盒子内部的一根轴转动,同时整个盒子再绕另一个轴转动。这种组合运动的结果是物体简单地围绕某一个新的轴转动。这个新的轴的奇特之处可以这样来描写:假如以z 方向上的一个矢量来表示在xy 平面内的转动率,并令其长度等于在该平面内的转动率,再在y 方向上画出另一个矢量,以表示在zx 平面内的转动率,则按照平行四边形法则把它们加起来,得出的矢量其大小就表示物体转动的快慢,其方向则代表转动是在哪个平面中进行的。简言之,角速度是 一个矢量,而在三个平面内转动的快慢,就是该矢量在垂直于各个平面的方向上的投影 [1] 。
作为角速度矢量的一个简单应用,我们可以计算一下作用在一个刚体上的转矩所消耗的功率。功率当然是功随时间的变化率,在三维空间中,可以证明功率是P =τ ·ω 。
所有平面转动的公式都可以推广到三维空间。例如,假定一个刚体以角速度ω 绕某一轴转动,我们可以问,“在矢径 r 处的一个点的速度是什么?”可以证明刚体上一个粒子的速度是 v = ω × r ,这里 ω 是角速度, r 是矢径,我们把它作为一个问题留给学生去证明。叉积的又一个例子是:科里奥利力的公式也可以把它写成叉积的形式: F c =2 m v × ω 。即假如一个坐标系以角速度ω 转动,一个粒子以速度v在这个坐标系内运动,在这个转动坐标系中考虑问题,就必须加上赝力 F c 。
§20-3 回转仪
现在再来讨论角动量守恒定律。这个定律可以用快速旋转的轮子或下面的回转器来演示(见图20-1)。假如我们站在一个转椅上,并拿着绕水平轴转动的轮子,这个轮子绕水平轴有一个角动量。绕竖直 轴的角动量不会因为椅子的支轴(无摩擦)而改变,假如我们把轮子的轴转到竖直方向,那么轮子就具有绕竖直轴的角动量,因为这时它在绕竖直轴转动。但是,这个系统 (轮子,我们自己和椅子)不可能 有竖直分量的角动量,因此,我们和椅子必须沿与轮子自旋相反的方向转动,以与轮子的转动平衡。
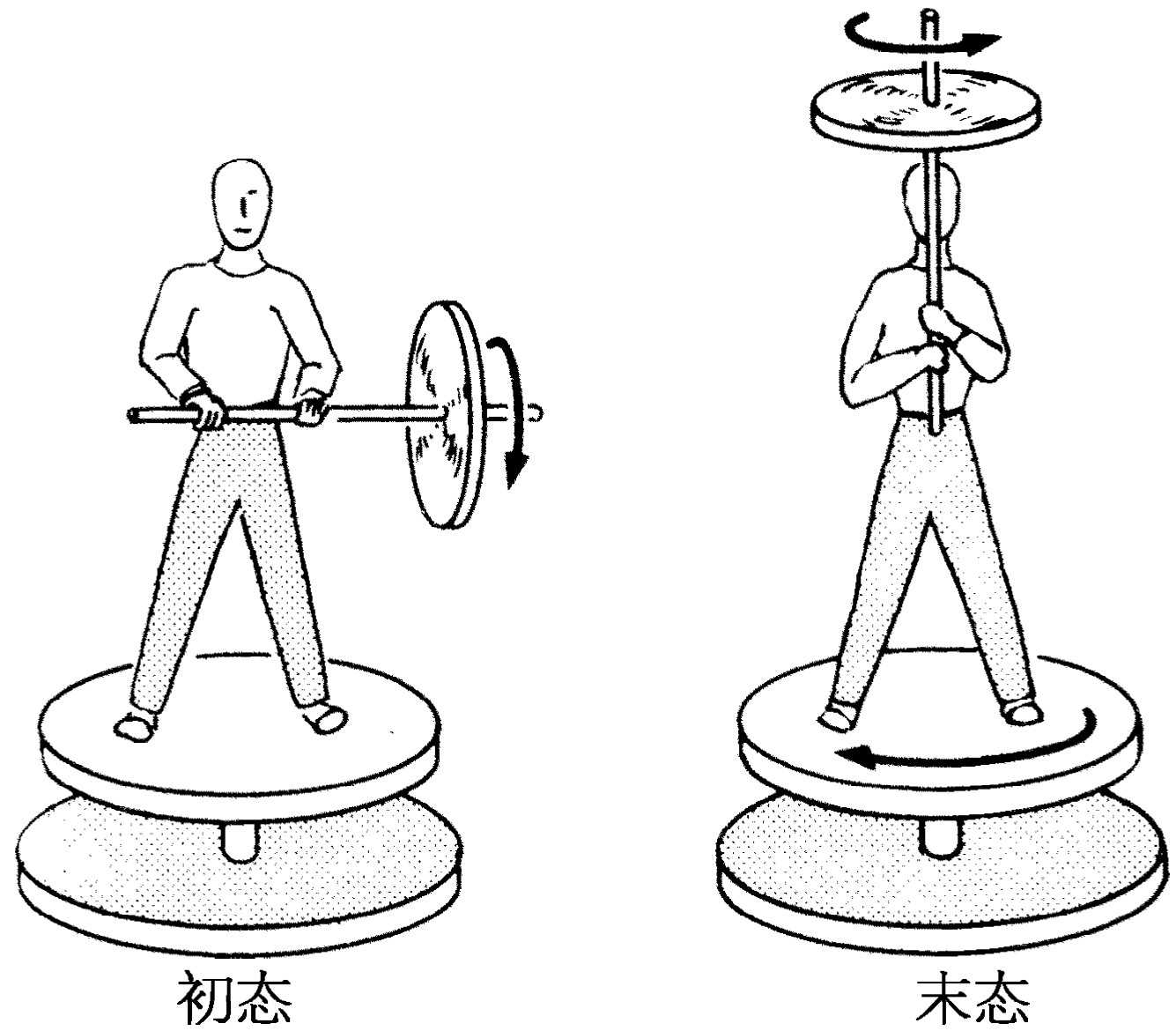
图20-1 起先 :轴是水平的,绕竖直轴的转矩等于0;后来 :轴在竖直方向,绕竖直轴的角动量仍然为零,人和椅子的转动方向与轮子的转动方向相反
首先我们来较详细地分析一下刚才叙述的事情。使我们感到惊奇和需要理解的是,当我们把回转仪的轴转向竖直方向时,从哪里来的力使我们和椅子转动的。图20-2表示轮子绕y 轴快速转动。因此,它的角速度是沿着绕它转动的轴,结果表明它的角动量也同样在y 方向上。现在假如我们想使轮子以很小的角速度Ω 绕x 轴转动,那么需要多大的力呢?在经过一个很短的时间Δt 之后,轴转到一个新的位置,与水平方向成Δθ 角。因为角动量的主要部分是由于绕轴旋转而产生的(很小一部分是由慢慢转动引起的),所以我们看到角动量矢量发生了变化。角动量发生了什么变化呢?角动量的大小 没有变,但是它的方向 改变了Δθ 。这样,矢量ΔL 的大小为ΔL =L 0 Δθ ,因此,转矩,即角动量随时间的变化率是
τ =ΔL /Δt =L 0 Δθ /Δt =L 0 Ω .
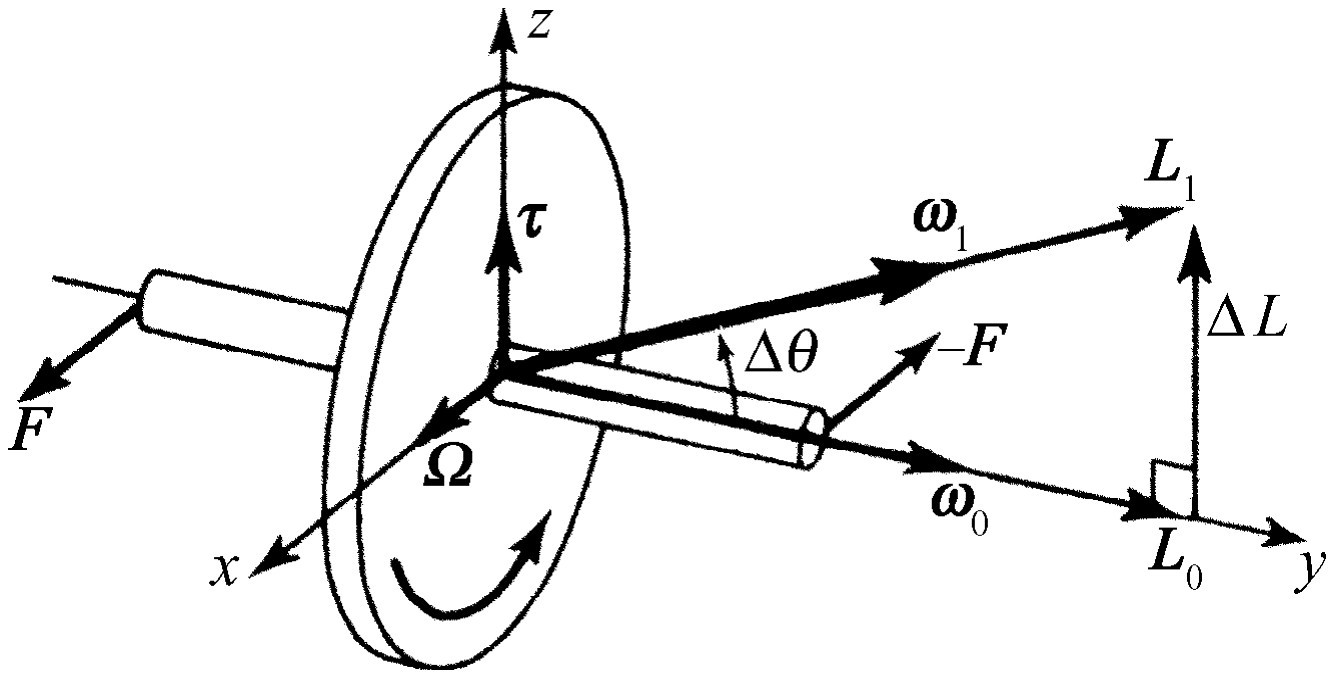
图20-2 回转仪
考虑到各个量的方向,我们知道
τ = Ω × L 0 .(20.15)
由此可见,如果 Ω 和 L 0 如图所示,都在水平方向,τ 就在竖直 方向。为了产生这个转矩,一定要有水平方向的力F 和-F 作用在轴的两端。这些力是如何作用的呢?在我们试图使轮子的轴往竖直方向转动时,通过我们的手施加了这种作用力。但是,牛顿第三定律要求有大小相等、方向相反的力(和大小相等、方向相反的转矩 )作用在我们身 上。这就使我们绕竖直轴z 沿相反方向转动。
这个结果可以推广到快速旋转的陀螺上去。对于常见的旋转陀螺,作用在它质心上的重力提供了一个相对于与地板接触点的转矩(见图20-3)。这个转矩在水平方向,它使陀螺的轴绕竖直方向在一个圆锥上进动。假如 Ω 是(竖直方向的)进动角速度,我们再次发现
τ =d L /dt = Ω × L 0 .
因此,当我们对快速旋转着的陀螺施加转矩时,其进动方向就在转矩的方向上,也就是与产生转矩的力垂直的方向。
现在我们可以说是理解了回转仪的进动,实际上,我们是从数学上去理解的。然而,这只是数学上的事情,而且在某种意义上简直是“奇迹”。当我们深入到越来越高级的物理学时,将会看到很多简单的东西用数学的方法来推导要比从基本的或简单的意义上去真正理解它们来得快一些。这是一个很奇怪的特性,而且在我们接触越来越高深的研究工作时,就会遇到这些情况,其中数学导出了结果,但这些结果没有一个人能以任何直接的方式真正理解它。狄喇克方程就是一个例子,它的形式非常简单而优美,但是它的结论却很难理解。对于我们所讨论的特殊情形,陀螺的进动看上去像是包含有直角和圆周,扭转和右手螺旋的一类奇迹。我们要做的是怎样用更符合物理的方式去理解它。
怎样用实际的力和加速度来说明转矩呢?我们注意到,当轮子进动时,在轮子上的质点并不是真正在一个平面内运动,因为轮子正在进动(见图20-4)。正如我们在前面(图19-4)所解释过的那样,穿过进动轴的质点沿曲线路径运动,从而要求有一个侧向作用力。这个力是通过我们推轴时施加的,它通过轮子的辐条传到轮子的边缘。“等一等”,也许有人要问,“在轮子的另一侧往相反方向运动的粒子的情况如何呢?”不难确定必须有一个沿反方向 的力作用在那一边。因此,我们所应施加的合力为零。这些力 相互抵消,但是其中的一个力必须作用在轮子的一边,另一个力作用在轮子的另一边。我们可以在轮子上直接用力,但是因为轮子是固体,它的辐条可以传递力,这就使我们可以通过推轴而施加力。
到目前为止,我们已经证明了,假如轮子在进动,它就能够与重力转矩或某种其他转矩相平衡。但是,我们所证明的这一切只是方程式的一个 解。即,假如有转矩作用,并且恰当 地使轮子开始旋转 ,那么它将平稳地和均匀地进动。但是我们并没有证明(而且这是不对的),由于一个给定转矩的作用,自旋物体可能进行的最 一般运动就是均匀进动。一般运动还包含有相对于平均进动的“晃动”。这个“晃动”称为章动 。
有人喜欢说,当人们在回转仪上施加一个转矩时,它就转动,并进动,即这个转矩产生了进动。非常奇怪的是,当突然把回转器放开的时候,它不是在重力的作用下下落 ,而是向旁边运动!为什么我们所知道 并感觉 到的向下 的重力会使它侧向运动呢?世界上像式(20.15)之类的所有公式都不能回答这个问题,因为式(20.15)是一个特殊方程,仅在回转仪正常进动时才适用。说得详细一点,所发生的真实情况如下:假如我们紧紧抓住轴使其不能以任何方式进动(但是陀螺在自旋),这样就没有转矩作用着,甚至连重力转矩都没有,因为它被我们的手指平衡了。但是,在我们突然把手放开的一瞬间,立即就有一个重力转矩。任何头脑正常的人都会认为陀螺将掉下来,确实如此,当陀螺自转不太快时,确实看到它在开始时是在下落。
正如我们预期的那样,回转器确实是在下落。但当它一旦下降时,它就开始转动,假如要使这个转动继续下去,就需要有一个转矩。由于在这个方向上没有转矩,回转仪就沿与失去的力相反的方向“落下”。这就使回转仪有一个绕竖直轴运动的分量,就像在稳定进动时一样。但是,实际运动要“超过”稳定的进动速度,实际上轴又再升回到原来开始时的水平位置。轴的一端所走的路径是一条摆线(即像粘在汽车轮胎上的石子所走过的路径)。通常这种运动很快,以致眼睛无法跟踪,而且由于滚珠轴承的摩擦力,使它很快衰减下来,变成稳定的进动(图20-5)。轮子旋转得越慢,章动就越明显。
当运动稳定之后,回转仪的轴要比开始时略低一点。为什么呢(这里有更复杂的细节,我们所以要进行讨论是为了不使读者产生回转仪是绝对不可思议的奇迹的想法。它确实是 很奇特的,但绝非不可思议的奇迹)?假如我们绝对水平地抓住回转仪的轴,然后突然放开,那么简单的进动方程就可以告诉我们,它是在水平面内进动的。然而这是不可能的!轮子对于进动轴有一定 的转动惯量,这一点尽管前面忽略了,但确是存在的,如果它相对于这个轴转动,即使很慢,它对这个轴也有一个比较弱的角动量。这个角动量是从哪里来的呢?如果支轴很理想,相对于竖直轴就没有转矩。如果角动量不变,进动是 怎么来的呢?回答是轴端的摆线运动衰减为等效的滚动圆中心的平均和稳定的运动。也就是说,它处于略为低一点的位置上。因为它较低,自旋角动量就有一个微小的竖直分量,这正是进动所需要的。这样,你就明白,为了继续保持转动,必须使它低一些,同时向重力作一点让步;通过把它的轴放低一些来保持其绕竖直轴的转动,这就是回转器的旋转过程。
§20-4 固体的角动量
在我们结束三维空间转动的课题之前,我们至少还要定性地讨论几个在三维转动中发生的效应,这些效应本身不是自明的。一般说来,主要的效应是一个刚体的角动量并不一定 必须和角速度在同一个方向上。我们来考虑一个轮子,这个轮子倾斜地固定在一根杆上,但轴通过其重心,如图20-6所示。当我们使轮子绕轴旋转时,任何人都知道,因为轮子倾斜地安装着,轴承将发生震动。定性地说,我们知道在转动系统中有一个离心力作用在轮子上,试图把轮子上的物体抛到离轴尽可能远的地方。这趋向于使轮子的平面排成与轴相垂直。为了反抗这种趋势,轴承就要施加一个转矩。如果轴承施加了转矩,必然会有一个角动量的变化率。当我们仅使轮子绕轴旋转时,怎么会有角动量的变化率呢?假使我们把角速度ω 分成ω 1 和ω 2 ,ω 1 垂直于轮子的平面,ω 2 平行于轮子的平面。什么是角动量呢?相对于这两个轴的转动惯量是不同的,因此,角动量的两个分量(只在这两个特殊的轴上)等于转动惯量乘相应的角速度分量,它们的比值与角速度分量之比值不一样 。因而角动量矢量在空间的方向不是 沿着轴的方向。当我们转动物体时,我们也在空间中转动了角动量矢量,这就必须在轴上施加一个转矩。
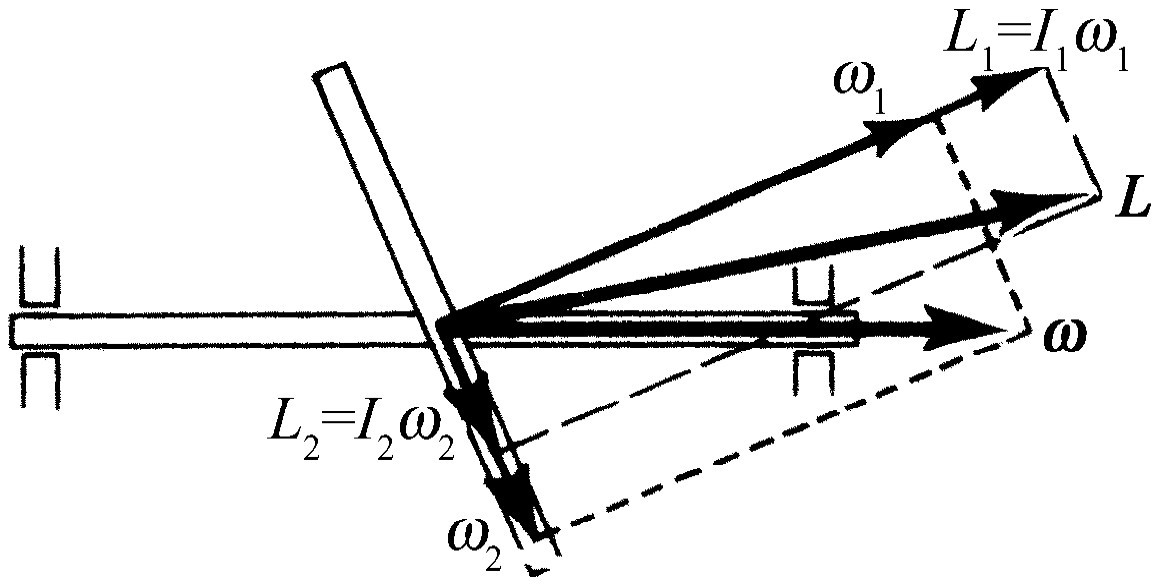
图20-6 一个转动物体的角动量并不一定平行于角速度
转动惯量有一个非常重要而有趣的性质,很容易叙述,也很容易应用,它是上述分析的基础,但它太复杂,难于在这里证明。这个性质叙述如下:任何刚体,即使是像马铃薯之类不规则的物体,都有通过质心的三根互相垂直的轴,使得相对于这三根轴中某一根轴的转动惯量与通过质心的任何轴相比具有最大 可能值;相对于这三根轴中另一根轴的转动惯量则具有最小 可能值;而对于第三根轴的转动惯量则处于两者之间(或等于其中之一)。这三根轴称为物体的主轴 ,它们具有一个很重要的性质——如果物体绕其中一个轴转动,它的角动量与角速度的方向相同。对于具有对称轴的物体来说,它的主轴就是对称轴。
假如我们用x ,y 和z 轴来表示主轴,并称相应的主转动惯量为A ,B 和C ,我们就能很容易算出以任一角速度ω 转动的物体的角动量和动能(图20-7)。如果将ω 沿x ,y ,z 方向分解成ω x ,ω y ,ω z 分量,并在x ,y ,z 轴上取单位矢量 i , j , k ,我们就可以把角动量写成
 (20.16)
(20.16)
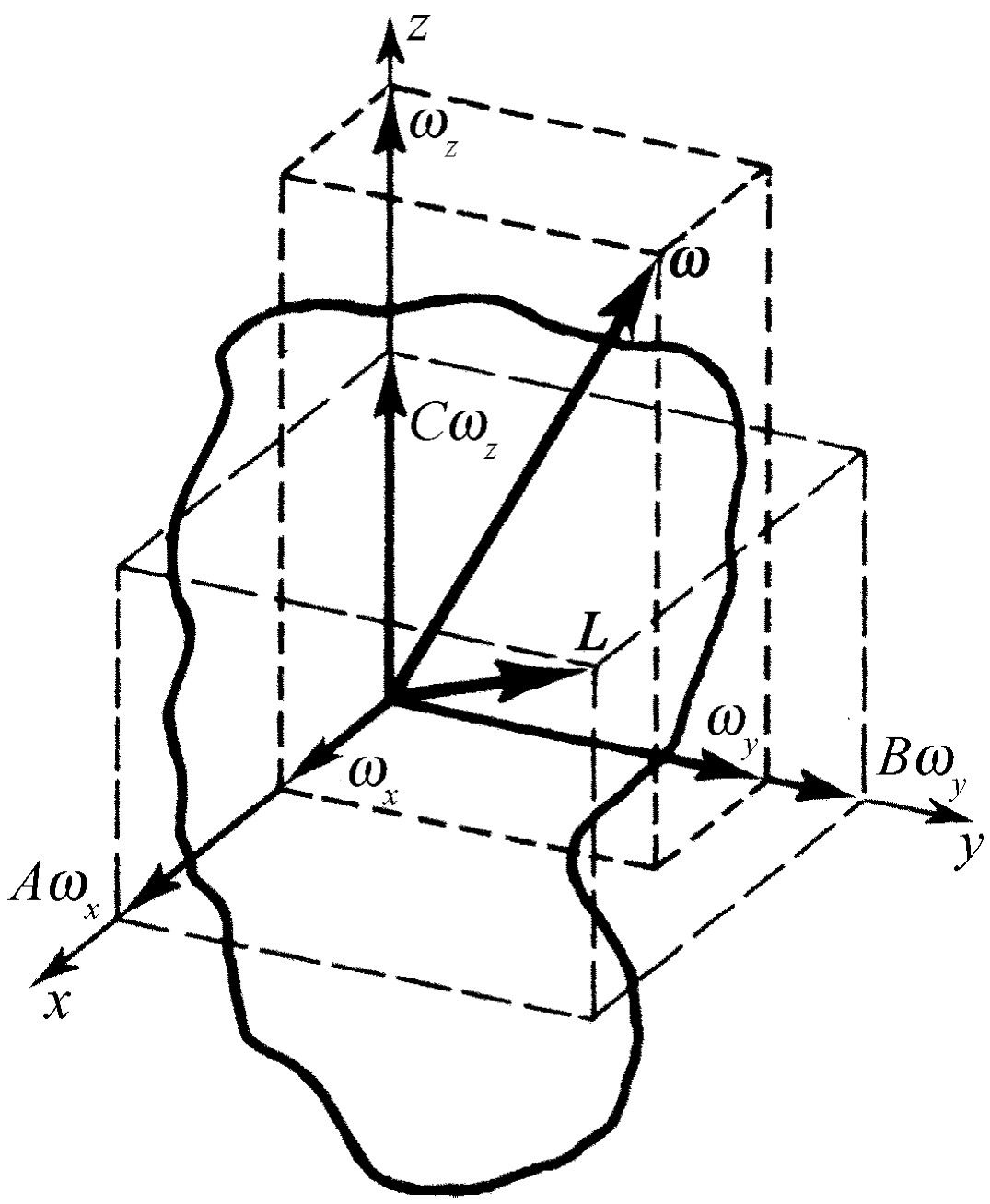
图20-7 一个刚体的角速度和角动量(A >B >C )
转动动能是
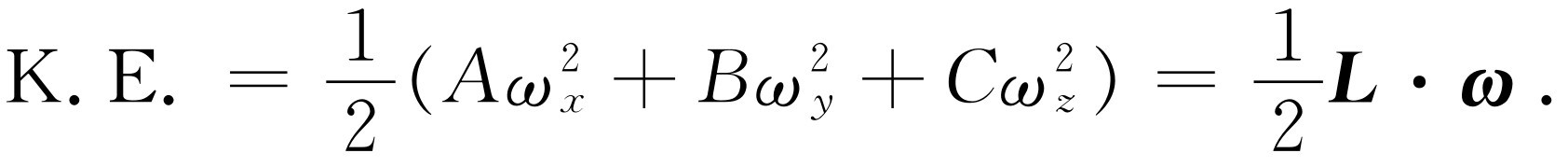 (20.17)
(20.17)


