第27章 几何光学
§27-1 引言
本章将用所谓几何光学 近似来讨论上一章的概念对许多实际装置和仪器的一些初步应用。这种近似是许多光学系统和仪器在其具体设计中最有用的一种方法。几何光学要么十分简单,要么非常复杂。这样说的意思是,或者我们只是很肤浅地学习它,使得我们利用它的一些规则就能粗糙地设计仪器,而这些规则又非常简单,以致在这里根本没有必要去讲述它们,因为它们实际上是中学水平的内容;或者如果我们想要知道透镜以及类似器件的微小误差,则题材又太复杂,以致在这里讨论它显得太深!如果有人想解决一个在透镜设计方面实际而详细的问题,包括像差分析在内,那么奉劝他去阅读有关著作,要不就利用折射定律找出光线通过各个表面的轨迹(这就是本书所要讲的做法),并求出它们从哪里射出以及是否形成一个满意的像。有人说这太麻烦了,但今天借助计算机,这是解决问题的一个正确的方法。人们可以提出问题,并且很容易一条光线接着一条光线地进行计算。因而问题最终确实变得十分简单,也用不到什么新的原理。而且事实证明,不论是初等还是高等光学,它们的规则对于别的领域来说,很少有什么特色,所以没有什么特殊的理由要把这一题材讲得太深,但有一个重要的例外。
几何光学最高深和抽象的理论是由哈密顿(W.R.Hamilton)完成的,结果证明,这种理论在力学中有很重要的应用。实际上它在力学中甚至比在光学中更为重要,所以我们把哈密顿理论作为高等分析力学课程的一部分放到高年级或研究班去讲。在估计到几何光学除了为本身的目的以外很少有贡献之后,现在我们就在上一章所概括的原理的基础上对简单光学系统的基本性质进行讨论。
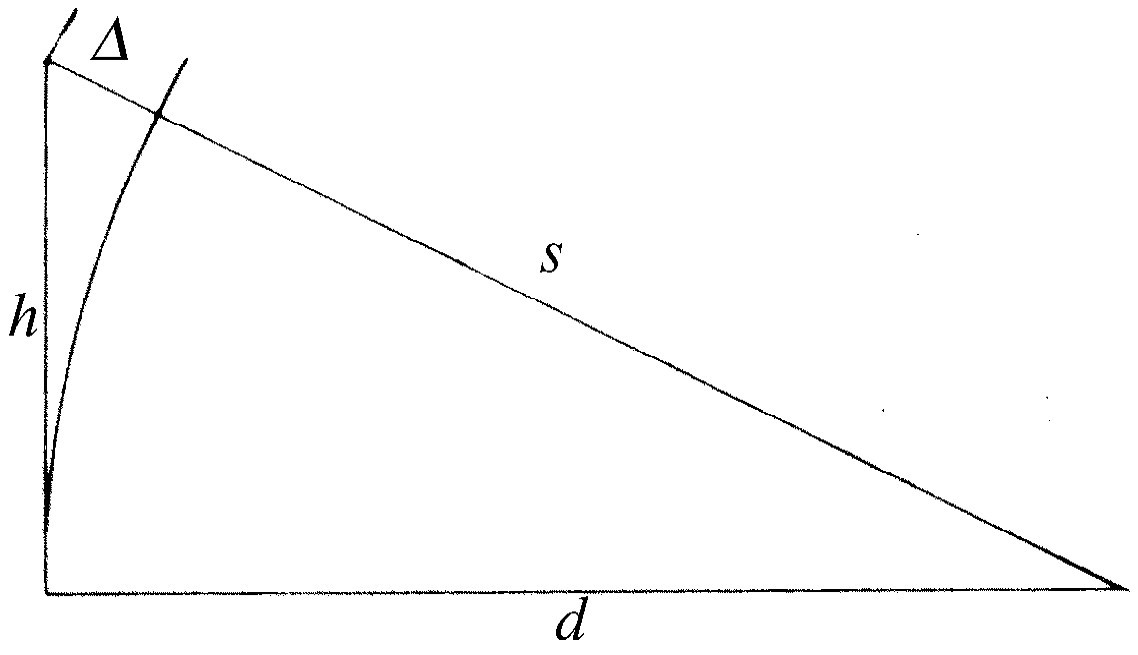
为了进行讨论,就必须有一个几何公式,其内容如下:如果有一个高(h )很小而底边(d )很长的直角三角形,则斜边s (我们在求两条不同路径之间的时间差时将用到它)比底边长(图27-1)。长多少呢?其差值Δ =s -d 可以用许多方法来求得。其中一种方法是这样:由图可见s 2 -d 2 =h 2 ,或(s -d )(s +d )=h 2 ,但s -d =Δ ,而s +d ≈2s ,于是
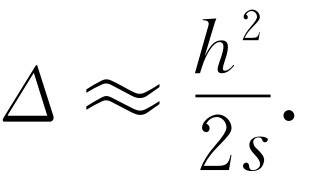 (27.1)
(27.1)
这就是讨论曲面成像时所需要的全部几何学!
§27-2 球面的焦距
我们所要讨论的第一个而且最简单的情况,是把两种折射率不同的介质分开的那种单折射面(图27-2)。我们把具有任意折射率的情况留给学生去做,因为最重要的往往是概念 而不是特殊情况,并且这样的问题在任何情况下解决起来都是很简单的。所以我们假定光在左方的速率为1,在右方的速率为1/n ,这里n 是折射率。光在玻璃中传播较慢,要小一个因子n 。
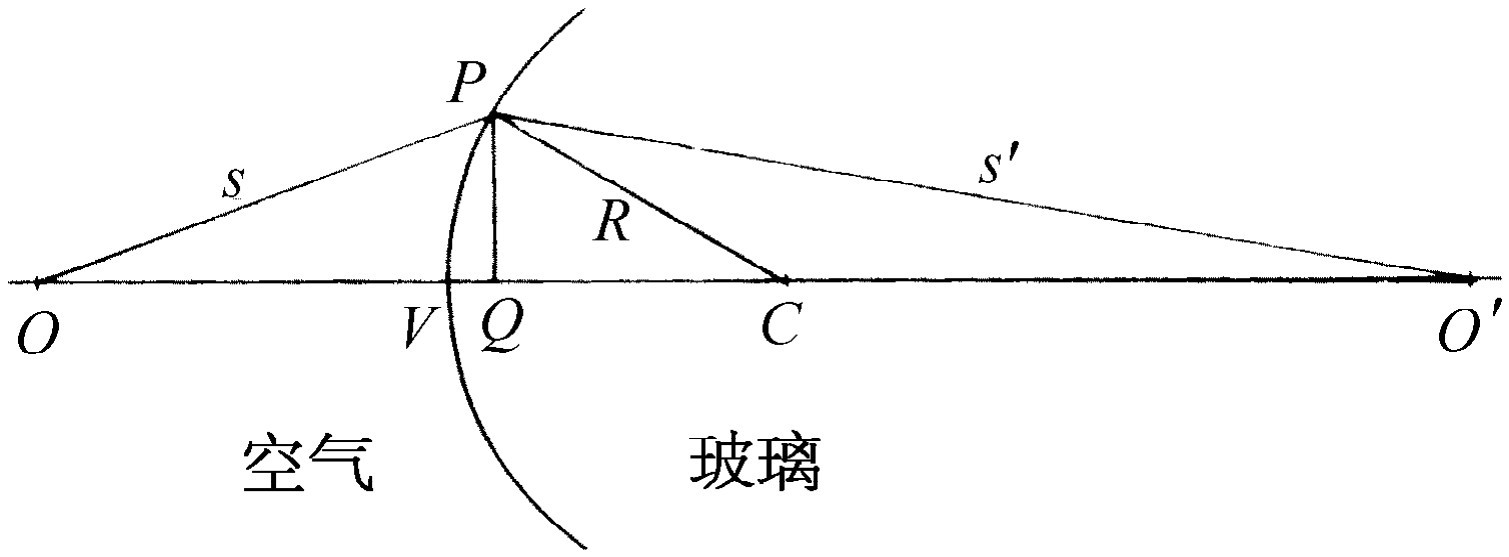
现在假定有一O 点在玻璃表面之前距离s 处,另一点O′ 在玻璃之内距离s ′处。我们想这样来设计一个曲面,使每条从O 点射到表面上任何一点P 处的光线经折射后都行进到O ′点。为了做到这一点,必须使表面具有这样的形状,使光从O 走到P 所花的时间,亦即距离OP 除以光的速率(这里光速为1),加上n ·O ′P ,也就是光从P 走到O ′所花的时间,等于一个常数(与P 点无关)。这一条件为我们决定表面的形状提供了一个方程。它的解告诉我们此表面是一个非常复杂的四次曲面,学生如有兴趣可用解析几何来进行计算。但是如果计算一个对应于s →∞的特殊情况,那么事情就比较简单,因为这时的曲面是一个二次曲面,我们对它比较熟悉。如果将这个曲面与当光来自无穷远时我们所求得的聚焦镜的抛物面进行比较,则是令人十分感兴趣的。
因而正确的表面不易制造,因为要把光从一点聚焦到另一点需要相当复杂的表面。事实证明,我们在实践中一般并不试图去制造这种复杂的表面,而作一妥协。我们不想把所有 的光线都聚焦到一点,而是这样做,使得只有相当靠近OO′ 轴的光线聚焦到一点。遗憾的是,离轴较远的光线即使想要聚焦到一点也会偏离,因为理想的表面很复杂,而我们只是用了一个在轴上具有适当曲率的球面来代替它的缘故。制造一个球面要比制造其他曲面容易得多,因此找出射到球面上的光线将会出现什么情况对我们是有用的,我们假定只有靠近轴的光线被完全聚焦。靠近轴的那些光线有时叫做傍轴光线 ,而我们所分析的就是傍轴光线聚焦的条件。以后我们还将讨论不是所有光线都是傍轴的情况下所导致的误差。
因此,假定P 靠近轴,我们作垂线PQ ,使PQ 之高为h ,并暂且设想表面是一个通过P 的平面。在这种情况下,从O 到P 所需的时间将超过从O 到Q 的时间,同样,从P 到O′ 的时间亦将超过从Q 到O ′的时间。但这正是玻璃所以必须弯曲的原因,因为所超过的总的时间必须由从V 到Q 所延迟的时间来补偿!现在沿路径OP 所超过的 时间为h 2 /2s ,而在PO′ 路径上所超过的时间为nh 2 /2s′ 。所超过的时间必须与沿VQ 所延迟的时间相抵消,而此延迟时间与在真空中的不同,因为有介质存在。换句话说,光从V 行进到Q 的时间不是像它直接在空气中行进时一样,而是比之慢了n 倍,所以在这段距离内剩余的延迟时间为(n -1)VQ 。但VQ 有多长?如果点C 为球心,R 为其半径,那么由同一公式我们可以看到这段距离VQ 等于h 2 /2R ,因此我们发现联系距离s 与s′ 而又给出所需表面的曲率半径R 的规律为
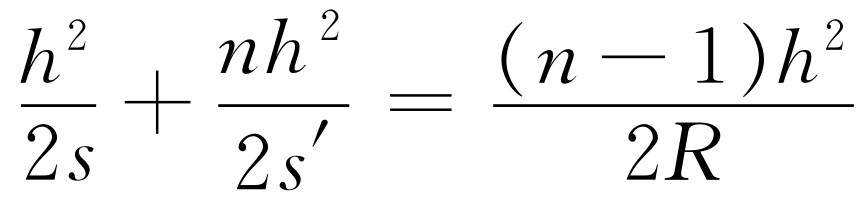 (27.2)
(27.2)
或
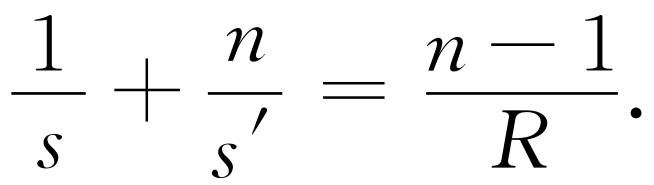 (27.3)
(27.3)
如果我们有一点O 及另一点O ′,并且想把光从O 点聚焦到O′ 点,那么就可用此公式来计算所需表面的曲率半径R 。
现在有趣的是,结果表明:具有同样曲率半径R 的同一透镜对于其他距离也能聚焦,也就是说,对于任何两个倒数之和(其中一个乘上n )为一常数的距离也能聚焦。因此,一个给定透镜(只要限于傍轴光线)不仅能把光从O 聚焦到O ′,而且也能把光在无数对其他点之间聚焦,只要这些成对的点满足1/s +n/ s′等于一个表征透镜特性的常数这个关系。
特别有趣的是s →∞的情况。由公式可见,当s 一个增加时,另一个则减少。换句话说,若点O 向外移动,点O ′就向内移动,反之亦然。当点O 移向无穷远时,点O ′在介质内也在移动,直到离表面一定距离为止,这段距离叫做焦距f ′ 。如果平行光入射时,它们将在距离f ′处与轴相交。同样,我们可以想象反方向的情况(请记住倒易规则:若光可从O 行进到O ′,当然也可从O ′行进到O )。因此,假定说玻璃内有一光源,我们也许想知道其焦点在哪里。特别是,如果光在玻璃内无穷远地方入射(同样的问题),它将聚焦在外面的何处?这个距离叫做f 。当然我们也可使光反方向而行之。若在f 处有一光源,把光射进表面,则它将以平行光束射出。我们很容易求出f 与f ′的数值为
 (27.4)
(27.4)
 (27.5)
(27.5)
从以上两式可以看到一个有趣的情形:如果把各焦距除以相应的折射率,即得相同的结果!事实上,这个定理是普遍成立的。它对任何透镜系统都是正确的,不论这一系统多么复杂,因而记住它是很有意义的。我们在这里并没有证明过它普遍成立——只是指出了对于单独一个表面,它是对的,然而碰巧它却普遍成立,以致系统的两个焦距就以这一方式互成关系。式(27.3)有时可写成下列形式
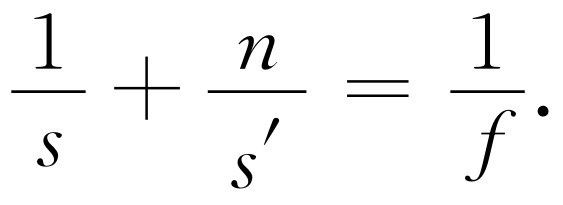 (27.6)
(27.6)
这种形式比式(27.3)更为有用,因为测量f 比测量透镜的曲率和折射率容易得多:如果我们对透镜的设计不感兴趣,也不想知道它如何制成,而只从架子上拿它来使用,那么我们感兴趣的量是f ,而不是n 与1和R !
如果s 变得小于f ,就会发生一种有趣的情况。那么发生什么情况呢?若s <f ,则(1/s )>(1/f ),于是s ′为负;方程指出光将只对负的s ′值聚焦,这究竟意味着什么!它意味着一件很有趣和很确定的事。换句话说,即使数值为负,上式仍不失为一个有用的公式。它意味着什么已在图27-3中表示出。如果从O 点画一些发散的光线,无疑它们要在表面上偏折,但它们不会聚焦成一点,因为O 太靠近表面,以致“超过了折成平行光”的范围。然而,它们却这样地发散出去,好像是从玻璃外面 一点O ′发出的。O ′是一个表观像,有时叫做虚像 。图27-2中的像O ′叫做实像 。如果光真的射向一点,那么它就是一个实像。但是如果光看来 好像来自 一点(与原来的点不同的一个虚构的点),那么它就是一个虚像。所以当s ′变成负时,就意味着O ′在表面的另一边,这样一切就妥当了。
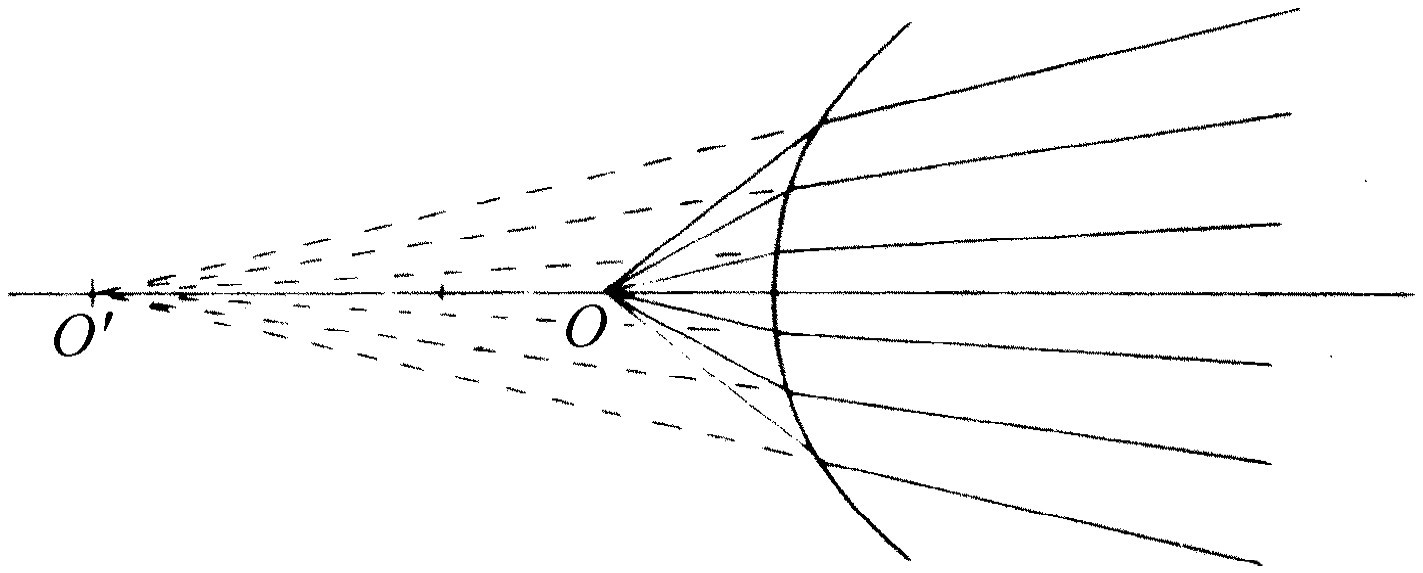
图27-3 虚像
现在我们来研究R 等于无限大时的有趣情况;此时1/s +n /s ′=0。换句话说s ′=-ns 。这意味着当我们从密介质朝疏介质看其中一个点时,这个点看来好像深了n 倍。同样,也可把同一个式子反过来用,因而当我们通过平表面看位于密介质内一定距离的物体时,它将看来好像光不是从那么深的地方射来的(图27-4)。当我们从上面看一个游泳池的底时,它看起来不像真的那么深,而只有原来深度的3/4,此即水折射率的倒数。
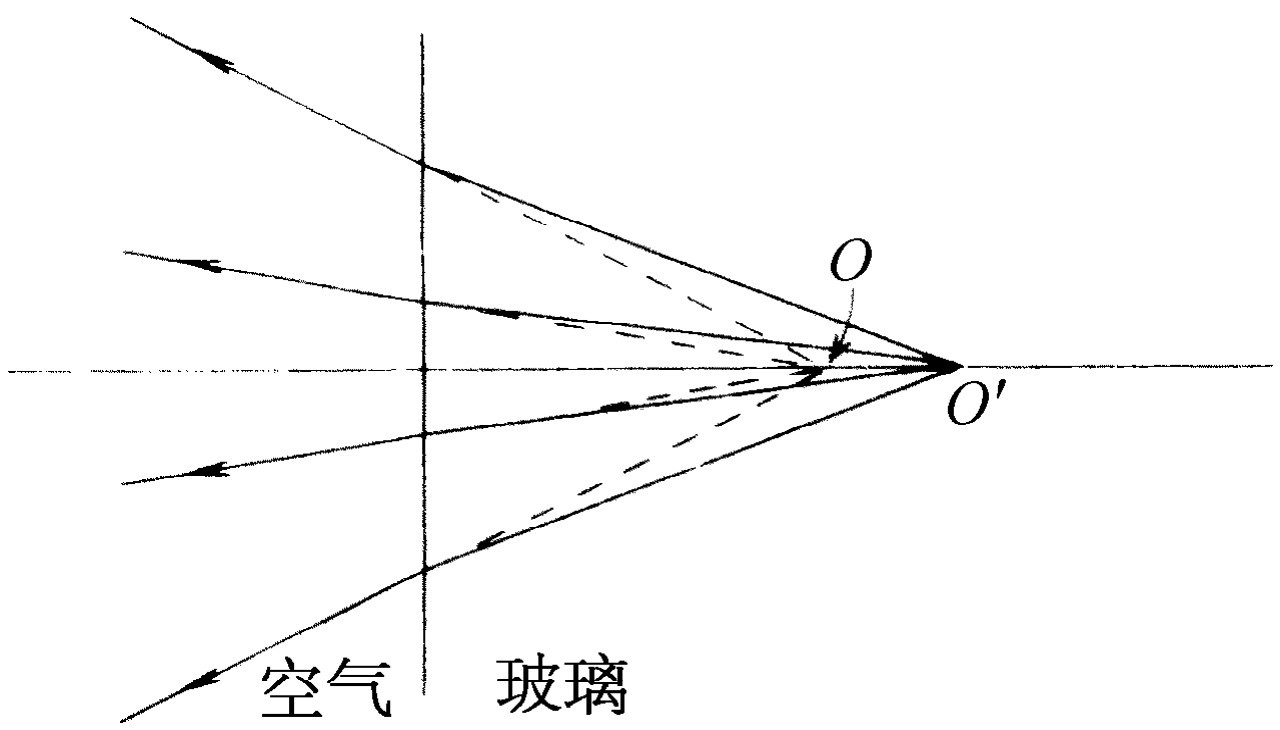
图27-4 一平表面把发自O ′的光重新成像为O
当然,我们可以继续来讨论球面镜。但是如果你理解了其中所包括的一些概念,那么你应能自己来解决这个问题。所以我们让学生自己去求出球面镜的公式,但我们指出,对于所涉及的一些距离,如果采用一定的习惯规则较为方便:
(1)若点O 在表面左方,则物距s 为正;
(2)若点O ′在表面右方,则像距s ′为正;
(3)若球面中心在表面右方,则表面曲率半径为正。
例如,在图27-2中,s ,s ′和R 皆为正;在图27-3中,s 和R 为正,而s ′为负。如果用一个凹表面,那么只要取R 为负值,公式(27.3)仍然会给出正确结果。
在应用上述习惯规则求球面镜的相应公式时,你将发现,如果在整个公式(27.3)中都令n =-1(好像镜子后面的介质的折射率为-1一样),那么结果就得出镜子的正确公式!
虽然利用最短时间原理来导出公式(27.3)既简单又优美,但用斯涅尔定律当然也能导出同一公式,只要记住一点,那就是这里角度很小,以致角度的正弦可用角度本身来代替。
§27-3 透镜的焦距
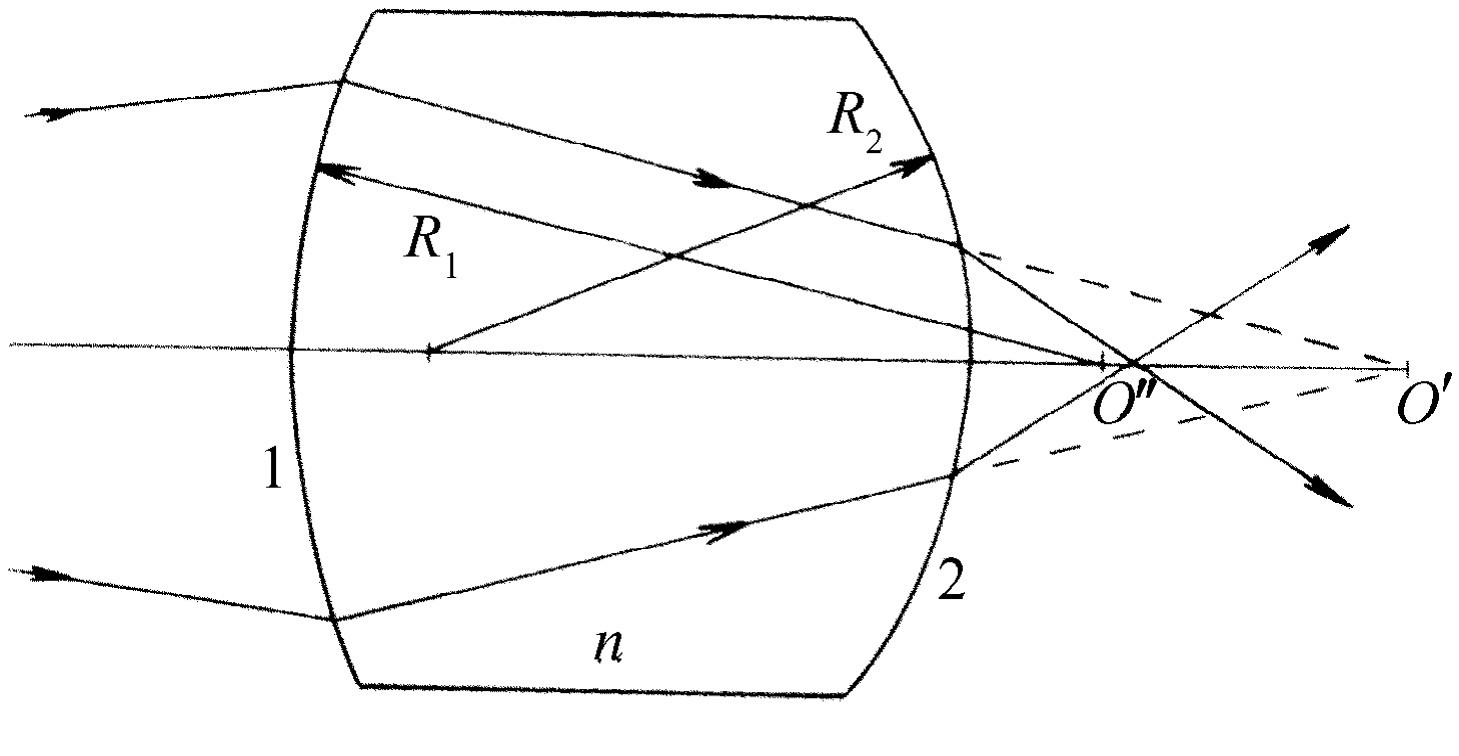
现在我们继续讨论另一种很实用的情况。我们所使用的大多数透镜具有两个表面,而不是只有一个表面。这将对事情产生什么影响呢?假定有两个不同曲率的表面,它们之间的空间充满着玻璃(图27-5)。我们想研究从点O 向另一点O ″聚焦的问题。怎么做呢?回答是:首先,对第一个表面应用式(27.3)而不考虑第二个表面。这将告诉我们,从O 点发出的光好像是向另外某一点(比如说O ′)会聚的或者是从这一点散发出来的,完全依符号而定。现在我们来考虑一个新的问题,即在玻璃(光线在其中会聚到某一点O ′)与空气之间有另一个表面。这时,光线实际上将向何处会聚呢?我们再应用同一个公式!我们发现它们会聚在O ″点。这样,如果需要,只要一个接一个地连续使用同一个公式,就是一共通过75个表面也行!
有一些相当高级的公式,在我们或许要追随光线通过5个表面时,将在有限的生命中给我们节省许多精力,但是当这种问题发生时,还是跟着光线通过5个表面,比之去记忆许多公式容易得多,因为说不定我们将根本不需要去跟着光线通过任何表面!
在任何情况下,我们的原则是,当通过一个表面时,找到一个新的位置,即一个新的聚焦点,然后把这个点当作下一个表面的出发点,如此等等。既然在第二个表面上我们是从n 走到1,而不是从1走到n ,而且在许多系统中有不止一种玻璃,以致其折射率为n 1 ,n 2 ,…,那么为了实际做到这一点,我们的确需要把公式(27.3)普遍化,使之适用于两种不同折射率n 1 与n 2 的情况,而不是只有一种折射率n 的情况。不难证明,公式(27.3)的普遍形式为
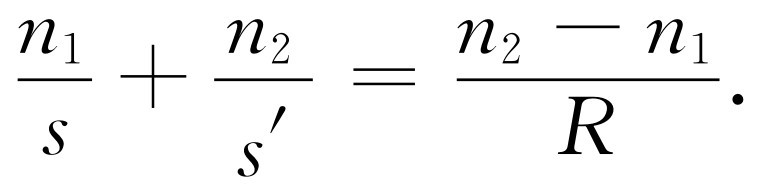 (27.7)
(27.7)
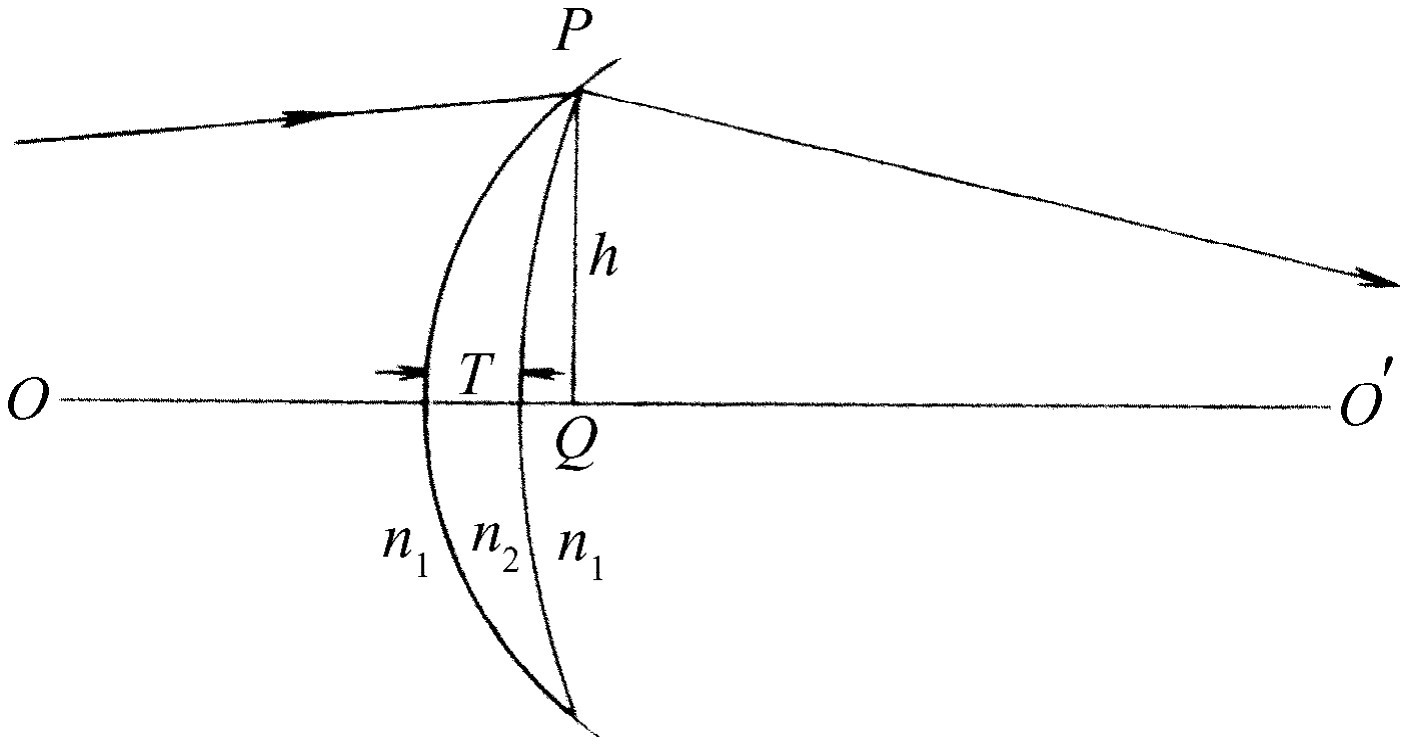
特别简单的是两个表面靠得很近的特殊情况。靠得如此之近,可以忽略由于厚度引起的微小误差。如果把透镜画成如图27-6所示的那样,我们可以提出这样的问题:透镜必须怎样制成才能使光从O 点聚焦到O ′点?假定光正好到达透镜的边缘P 点。暂且忽略折射率为n 2 、厚度为T 的玻璃的存在,则光从O 行进到O ′所超过的时间是(n 1 h 2 /2s )+(n 1 h 2 /2s ′)。于是,为了使走直线路径的时间等于走路径OPO′ 的时间,必须用一片玻璃,它的中心厚度T 应该这样,即足以使光通过这一厚度所引起的延迟时间补偿上述过量时间。因此,透镜的中心厚度必须由下列关系给出
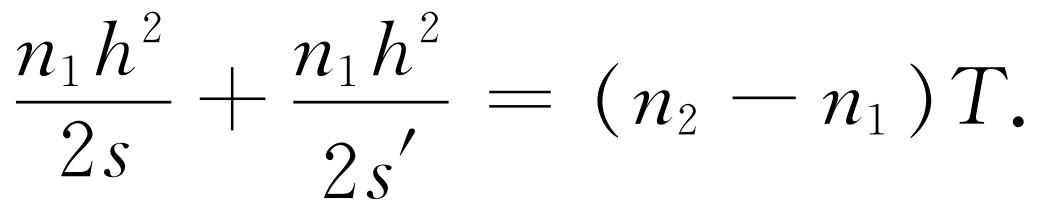 (27.8)
(27.8)
我们也可以用两个表面的半径R 1 与R 2 来表示T 。注意到习惯规则(3),对于R 1 <R 2 (凸透镜),得到
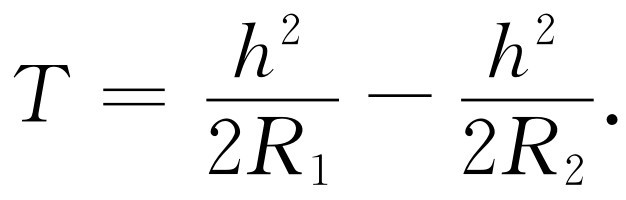 (27.9)
(27.9)
因而最后得到
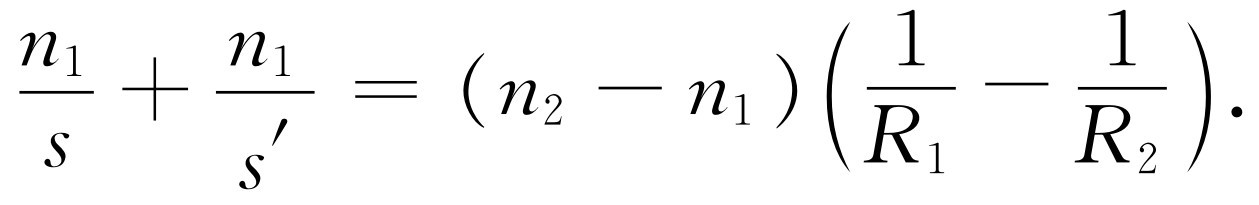 (27.10)
(27.10)
现在再记住当一点在无穷远时,另一点将在我们称之为焦距f 的地方。焦距f 由下式给出
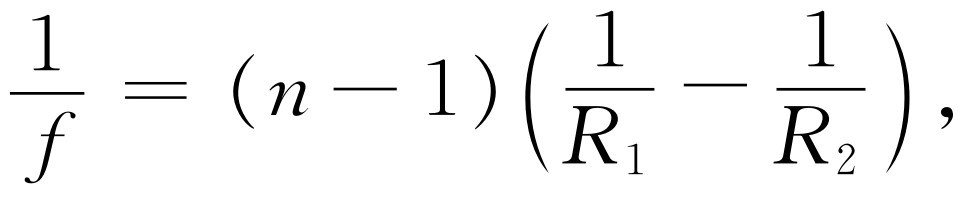 (27.11)
(27.11)
这里n =n 2 /n 1 。
如果现在取相反的情况,即s 趋于无穷远,则s ′等于焦距f ′。这时两焦距相等(这是两焦距之比等于光在其中聚焦的两介质折射率之比这一普遍规则的又一特殊情况)。在这一特殊光学系统中,初始和最后两个折射率都相同,因而两焦距也相等。
我们暂且把焦距的实际公式忘掉,如果我们购到一个由某人设计、具有某种曲率半径和某种折射率的透镜,那么我们可以这样来测量焦距,比如说观察一下无穷远处的一点聚焦在何处。一旦有了焦距,最好是直接用焦距写出我们的等式,于是这一公式为
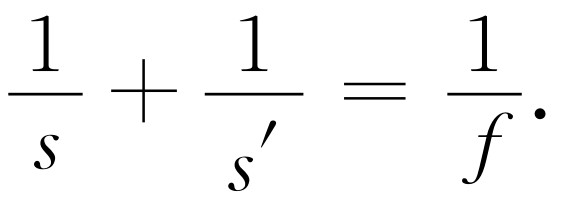 (27.12)
(27.12)
现在我们来看一下如何应用这个公式及其在不同情况下的含意。首先它指出,如果s (或s ′)为无穷大,则s ′(或s )为f 。这意味着平行光聚焦在距离f 处,实际上它定义 了f 。它告诉我们的另一有趣事情是,两个点(物点和像点)都朝同一方向运动。如果一点朝右运动,另一点也朝右运动。此外它还告诉我们若s 与s ′都等于2f ,则它们两者相等。换句话说,如果要得到一种对称情况,则我们发现它们都聚焦在距离2f 处。
§27-4 放大率
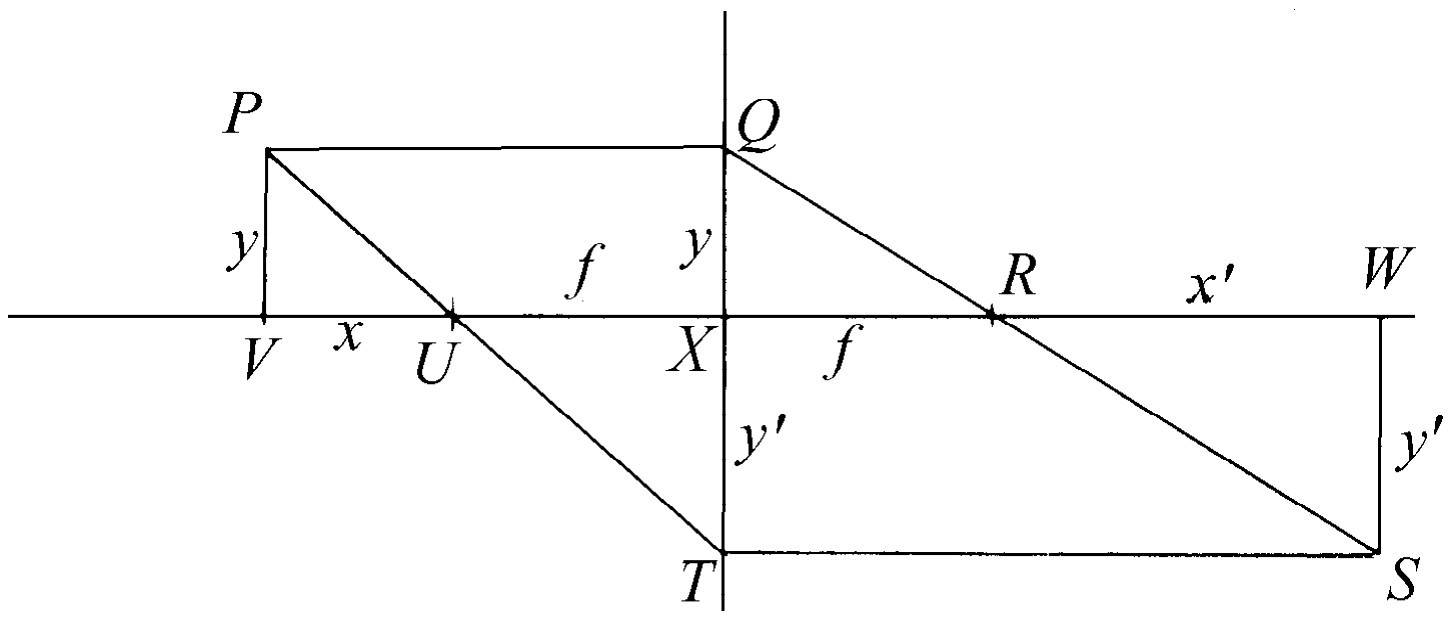
到现在为止,我们只讨论了轴上点的聚焦作用。现在我们来讨论不完全在轴上而稍为离开它一点的物体的成像,这样可以使我们了解放大率 的性质。当我们装置一个透镜把来自灯丝的光聚焦在屏上一“点”时,我们注意到,在屏上得到同一灯丝的“图像”,只是其大小比实际的灯丝大一些或小一些而已。这必然意味着从灯丝上每一点 发出的光都会聚到一焦点上。为了更好地理解这一点,我们来分析图27-7中所示的薄透镜系统。我们知道下列事实:
(1)从一边射来的任一平行于轴的光线都朝着另一边称为焦点的某一特殊点行进,这个点与透镜相距f 。
(2)任一从一边的焦点发出而到达透镜的光线,都在另一边平行于轴射出。
这就是我们用几何方法建立公式(27.12)所需要的全部知识,具体步骤如下:假定离焦点某一距离x 处有一物体,其高为y 。于是我们知道光线之中有一条光线(如PQ )将经透镜偏折而通过另一边的焦点R 。如果现在这个透镜能完全使P 点聚焦的话,那么只要找出另外一条光线的走向,就能找出这个焦点在哪里,因为新的焦点应在两条光线再次相交的地方。因此我们只要设法找出另外一 条光线的实际方向,而我们记得平行的光线通过焦点,反之亦然 :即通过焦点的光线将平行地射出!所以我们画出一条光线PT 通过U (诚然参与聚焦的实际光线可能比我们所画的两条光线的张角小得多,但它们画起来较为困难,所以我们假设能作这条光线)。既然它将平行射出,我们就画出TS 平行于XW 。交点S 就是所要求的点。这个点决定了像的正确位置和正确高度。我们把高度称为y′ ,离焦点的距离称为x′ 。现在我们可以导出一个透镜公式。应用相似三角形PVU 和TXU ,得
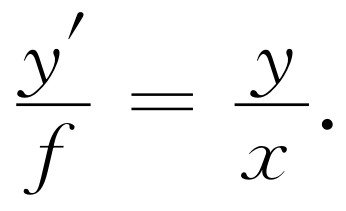 (27.13)
(27.13)
同样,从三角形SWR 和QXR ,得
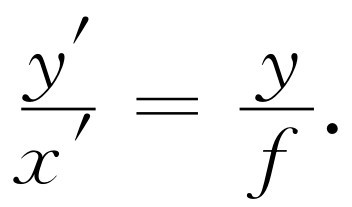 (27.14)
(27.14)
由此上两式各解出y ′/y 后,得
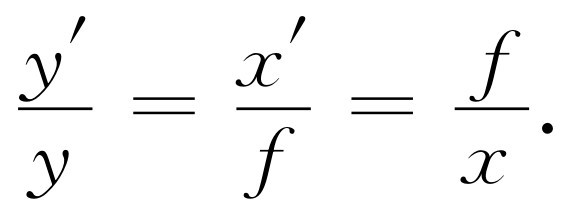 (27.15)
(27.15)
式(27.15)是有名的透镜公式;其中包括了我们关于透镜所需要知道的一切:它告诉我们放大率y ′/y ,用距离和焦距表示。它也把两个距离x 和x ′与f 联系起来
xx ′=f 2 ,(27.16)
这是一个用起来比式(27.12)简洁得多的形式。我们让同学自己去证明,若令s =x +f ,s ′=x ′+f ,则式(27.12)与式(27.16)相同。
§27-5 透镜组
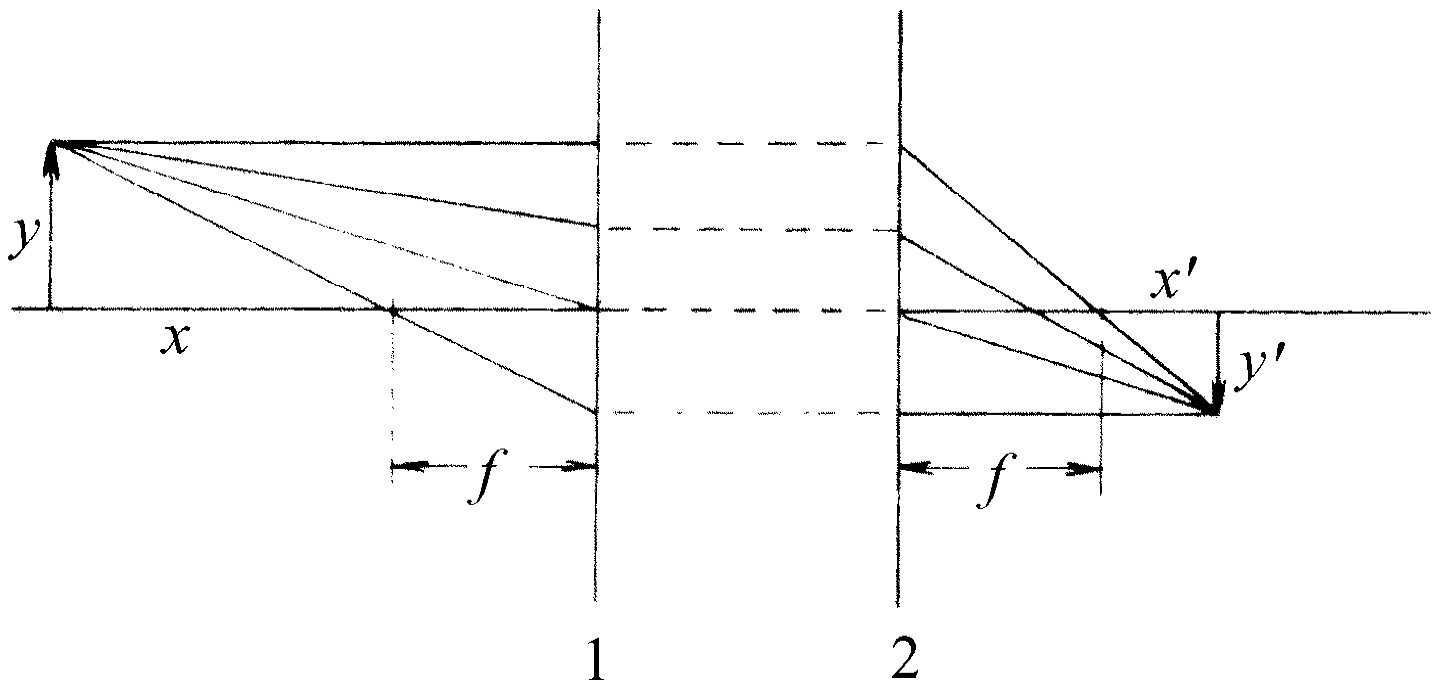
当有许多透镜时,我们将简短地叙述一下其一般的结果,而不加实际推导。如果有一个由几个透镜组成的系统,那么我们怎样来分析它呢?这很容易。先从某个物体开始,并利用式(27.16)或(27.12)以及任何别的等效公式,或者用作图法,算出它被第一个透镜成像在哪里。这样就得到一个像。然后把这个像作为下一个透镜的光源,并用第二个透镜(不管它的焦距是多少)再找出一个像。我们就这样对一连串透镜一直追踪下去。这就是要做的一切。由于它原则上没有什么新的东西,所以我们不准备深入下去。但是,就任一序列的透镜对于在某一介质例如空气中发出而终止在同一介质中的光所产生的各效应却有一个很有趣的最后结果。任何一种光学仪器——包括任意数目的透镜和反射镜的望远镜或显微镜——都具有下列性质:它有两个平面,叫做系统的主平面 (这些平面往往很接近第一个透镜的第一个表面和最后一个透镜的最后一个表面),它们具有下列性质:(1)如果光从第一边平行地射向系统,它就在一定的焦点射出,焦点位于离第二 主平面的距离等于焦距处,就好像这个系统是置于这一平面的一个薄透镜一样。(2)如果平行光从相反方向射来,那么它将会聚到离第一 主平面同一距离f 处的焦点上,又好像有一个薄透镜位于主平面处一样(见图27-8)。
当然,如果我们像以前一样测出距离x 与x ′,y 与y ′,那么对薄透镜所写的公式(27.16)在这里完全普遍适用,假定焦距从主平面而不是从透镜组中心算起的话。对薄透镜来说,两个主平面恰好重合。这种情况正像我们取来一个薄透镜,把它沿中间切开,再把它分开,而不去注意它已被分开一样。每一条射来的光线,会立即在第二个平面的另一边从光进入第一个平面的同一点突然射出!主平面与焦距可以用实验来求得,也可用计算来求得,于是光学系统的全部性质就此得到描述。当我们把这样巨大而复杂的光学系统处理完毕时,结果却并不复杂,这是一件很有趣的事。
§27-6 像差
在我们不致因透镜如此奇妙而感到过于兴奋之前,必须赶快补充一点,即透镜也有其严重的局限性,因为严格地说,我们的讨论只限于那些靠近轴的近轴光线。一个具有一定大小的真实透镜一般说来将显示出像差 。例如,在轴上的一条光线当然会通过焦点;一条很靠近轴的光线仍然也会很好地会聚到焦点上。但当光线离轴较远时,就开始偏离焦点,也许落到离透镜更近的地方,射到靠近透镜边缘上的光向下折射时将偏离焦点相当宽一段距离。因此,我们不是得到一个点像,而是得到一个模糊的光斑。这一效应称为球面像差 ,因为它是我们用以代替正确曲面的球面所具有的一种性质。对任一特定的物距来说,用修正透镜表面的形状,或者用几个透镜组合起来使各个透镜的像差趋于相互抵消的办法,球面像差可以得到纠正。
透镜还有另一个缺点:不同颜色的光在玻璃中具有不同的速率或不同的折射率,因而一个给定的透镜的焦距对不同的颜色是不同的。所以,如果我们把一个白的光点成像,其像将会有颜色,因为当我们使红光聚焦时,蓝光就不聚焦,或者反过来。这种性质叫做色像差 或色差 。
透镜还有其他一些缺点:如果物体在轴之外,那么当它离轴足够远时,聚焦实际上已不再很完善。验证这一点的最容易的方法是把一块透镜聚焦,然后把它偏转一下,以使光线与轴成大角度地射来。这时所形成的像一般都很粗糙,而且可能没有一个聚焦得很好的地方。因此,透镜中有好几种像差,以致光学设计者要用许多个透镜以补偿相互的像差的办法来加以校正。
要消除像差,我们必须谨慎到何种程度?是否可能构成一个绝对完善的光学系统?假定我们已经构成一个光学系统,并且认为它能把光正确地会聚到一点,那么,从最短时间的观点来论证,能否找到一个关于系统必须完善到什么程度的条件?这个系统总有某种形式的能使光进入的开孔。如果我们取离轴最远的光线,而它也能到达焦点(当然假定系统是完善的),那么对于所有光线,时间是正确相等的。但完全完善的东西是不存在的,所以问题在于,这条光线的时间可以差多少才不需要对它作进一步校正?这取决于我们所要成的像达到多么完善的程度而定。假定我们要使像做到尽可能地完善,那么,我们的想法当然是必须使每一条光线尽可能取几乎相同的时间。但结果证明这是不确切的,我们想做的事过于精细,以致超过了可能的限度,因为此时几何光学理论已不再适用!
记住最短时间原理并非是一种精确的表述,不像能量守恒原理和动量守恒原理那样。它只是一种近似 ,而寻求允许多少误差仍不致造成明显偏差倒是颇有意义的。回答是,如果我们作这样的安排,使得位于最边缘的光线——即成像最差的光线,也就是离轴最远的光线——与中心光线之间的时间差别小于与光的一次振动相应的周期,那么再作进一步改进已经无益。光是一种以确定频率振动的东西,这一频率与波长有关,如果我们已把系统安排得使不同光线的时间差别小于约一个周期,那么进一步改进系统已没有用处了。
§27-7 分辨本领
另一个有趣的问题——一个对于所有光学仪器都很重要的技术问题——是它们的分辨 本领 有多大。如果我们制造一架显微镜,就想看清楚所观察的物体,举例来说,这意味着,如果我们正在观察一个两端都有斑点的细菌,那么我们就要做到在把它们放大时能看清楚 有两个小点。人们也许会想,这只要把它们放足够大就行——我们总是可以再加上一个透镜,放大了又放大,而且凭着设计者的智慧,所有的球差和色差都可消除,因而没有理由说为什么不能不断地把像放大。所以显微镜的限度不在于不可能制造一个径向放大率大于2 000倍的透镜。我们能够制造一个径向放大率为10 000倍的透镜系统,但由于几何光学的局限性,以及最短时间原理并非精确成立这一事实,我们仍然 不能看清楚靠得太近的两个点。
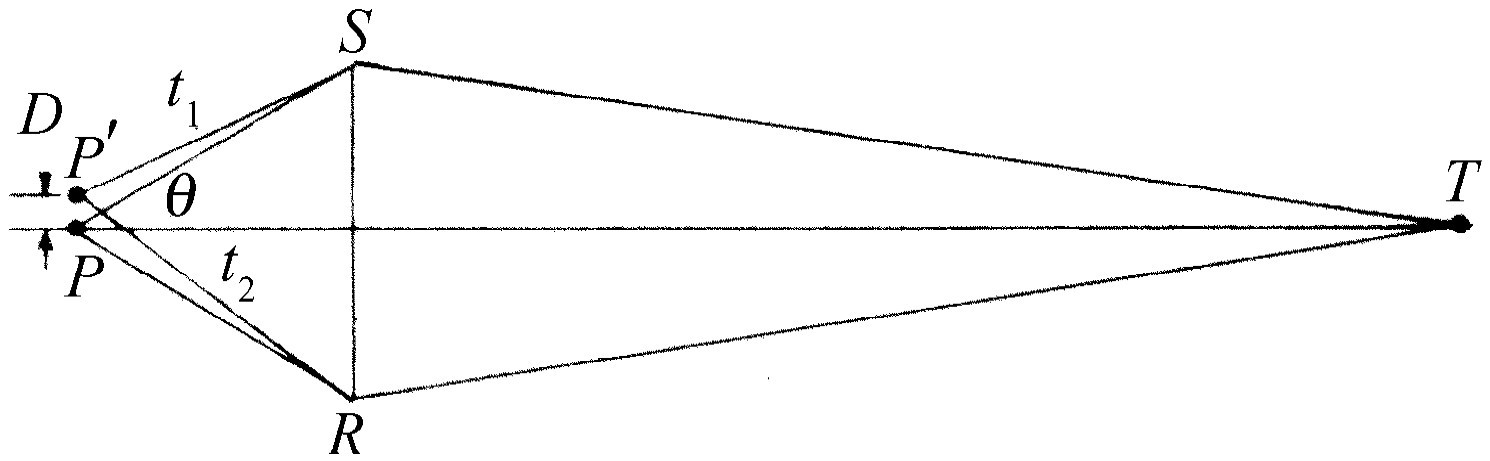
要找出用以决定两个点应分得多么开才能使它们的像看起来好像是分开的两个点的规则,可以结合不同光线所需的时间用一种很美妙的方法来叙述。假定现在不考虑像差,并设想对某一特殊点P 来说(图27-9),所有从物到像T 的光线所花的时间完全相同。(这是不确切的,因为它不是一个完善的系统,但那是另一个问题。)现在取附近另一个点P ′,并问其像是否能与T 分清楚。换句话说,我们是否能辨认出它们之间的差别。按照几何光学,当然应该有两个点像,但我们看到的可能是一个比较模糊的斑点,以致无从辨认出那里有两个点。第二个点聚焦在与第一个点显著不同的另一地方的条件是,对于通过透镜大开孔的两个边缘的极端光线P ′ST 与P ′RT ,光从一端行进到另一端所花的两个时间,必须与从两个可能的物点到同一给定的像点所花的时间不同 。为什么?因为,如果时间相同,两个物点当然都将聚焦 在同一点上。所以这两个时间不应相同。但它们必须相差多少才可以说两个物点不 都聚焦在同一点上,以致我们可以分清两个像点?对任何光学仪器,其分辨本领的一般规则是这样的:两个不同的点源,只有当一个点源聚焦在某一点,而从另一点源发出的两条极端光线到达这一点所花的时间与到达它自己的实际像点相比,相差大于一个周期时,才能被分辨。亦即顶端光线与底边光线到达非正确 焦点的时间差别必须大于某一数值,这个数值近似地等于光的振动周期
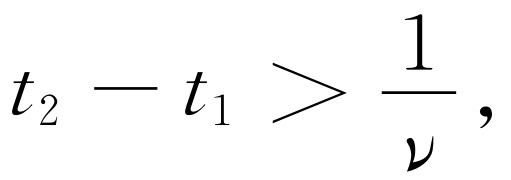 (27.17)
(27.17)
其中ν 是光的频率(即每秒的振动次数,也就是速率除以波长)。如果两点源之间的距离为D ,而透镜的张角为θ ,那么可以证明式(27.17)与D 必须大于λ /(n sin θ )的说法是完全等效的。这里n 是P 处介质的折射率,λ 是波长。所以我们所能看清楚的最小物体,其线度大约等于光的波长。望远镜也有一个相应的公式,它告诉我们恰好能分辨的两颗星的最小角差该为多少 [1] 。