第28章 电磁辐射
§28-1 电磁学
在物理学的发展中,最具戏剧性的时刻乃是不同现象得到高度综合的时刻,那时突然发现,以前看来似乎很不相同的现象,实际上只是同一事物的不同侧面而已。物理学史就是这种综合的历史,而物理科学所以能够取得成就,主要就是因为我们能够 进行综合。
19世纪物理学发展中最具戏剧性的时刻,也许是在1860年的某一天当麦克斯韦把电与磁的规律与光的规律联系起来的时候。这样一来,光的性质就被部分地阐明了。光,这个司空见惯而又难以捉摸的东西,它是那么重要而又神秘,以致在写《创世纪》的时候就觉得需要专门安排一天来创造它。然而当麦克斯韦完成他的发现时,他就可以说:“只要有了电与磁,就会有光!”
但是,为了达到这一登峰造极的时刻,却有一个逐渐发现并阐明关于电和磁的规律的漫长准备过程。这个准备过程我们留待下一学年去详细研究,现在仅简述如下。关于电和磁、电的斥力和引力以及磁力等等这些已被逐渐发现的性质表明,虽然这些力都很复杂,但它们都与距离平方成反比地衰减。例如我们知道,关于静止电荷的简单的库仑定律就表明,电力场的变化与距离平方成反比。因此,当距离足够大时,一个电荷体系对另一个电荷体系的影响就很小。当麦克斯韦试图把当时已经发现的所有方程或定律汇集在一起时,他注意到它们之间是相互矛盾的;为了使整个方程体系不矛盾,就必须在他所建立的方程中加进另外一项。于是,他就从这个新的一项得出了一个惊人的预言,那就是电场与磁场的一部分随距离的衰减远比反平方关系来得慢,也就是与距离的一次方成反比!因而他认识到,一处的电流可以影响远处的电荷,并且预言了我们今天所熟悉的一些基本效应——无线电传输、雷达,等等。
一个人在欧洲讲话,仅仅借助于电的影响,就能够被几千英里以外的洛杉矶的人听到,这好像是个奇迹。这怎么可能呢?这是因为场不是按距离平方成反比地变化,而是按距离一次方成反比地变化。最后,连光本身也被认识到是原子中的电子以非常惊人的快速振荡所产生的电磁扰动在空间的传播。所有这些现象我们可以概括为一个词:辐射 ,或更加明确地叫做电磁辐射 ,因为还有一两种其他辐射。但辐射一般都意味着电磁辐射。
这样一来,天地万物就被联系起来了。遥远星体上的原子运动仍能产生足够的影响以使我们眼睛中的电子运动,因而使我们看到了这些星星。如果这个规律不存在,我们就会对外部世界一无所知!甚至离我们50亿光年远的星系——这是我们至今所发现的最远的物体——中的电涌仍能影响射电望远镜前的大“圆盘”,使它产生足够大的、可以探测的电流。正因为如此,所以我们能够看到星体和星系。
这一值得注意的现象就是本章所要讨论的内容。在本物理课程开始的时候,我们曾给自然界描绘了一幅广阔的图画,我们现在已有较好的基础知识去了解它的某些方面,因此我们就来较详细地讨论它的某些部分。我们从19世纪末物理学所处的地位开始叙述。那时已经知道的基本定律可概括如下。
首先,有关力的定律:一是万有引力定律,我们已几次写过,即质量为M 的物体作用在质量为m 的物体上的力由下式给出
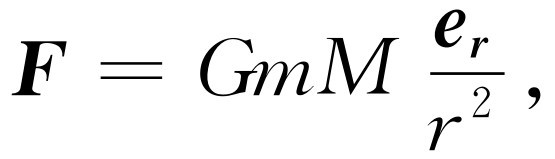 (28.1)
(28.1)
其中 e r 是由m 指向M 的单位矢量,r 为它们之间的距离。
其次,是关于电与磁的定律,在19世纪末所了解的情况是这样的:作用在电荷q 上的电力可用两个称为 E 和 B 的场及电荷q 的速度 v ,以下列等式描述
F = q ( E + v × B ).(28.2)
为使此定律完善,我们必须说明在给定情况下 E 和 B 的表示式。如果存在许多电荷,则 E 和 B 各为来自每个单独的电荷的贡献的总和。所以,如果我们能够找到单个电荷产生的 E 和 B ,只要将宇宙中所有电荷的效应加起来,就得到了总的 E 和 B !这就是叠加原理。
那么,由一个单独的电荷产生的电场与磁场的公式是怎样的呢?原来它很复杂,要懂得它必须做很多研究并花费许多精力。但这不要紧。我们现在写出这个公式来仅仅是为了使读者对大自然的美妙留下深刻的印象,我们之所以这样说,是因为我们可以 用读者现在所熟悉的符号在一页内概括所有的基本知识。这一关于由单独的电荷产生的场的定律就我们所知(量子力学除外)是完善而正确的,但它看上去相当复杂。现在,我们不准备研究所有的细节;我们写出它来仅仅是给读者一个印象,以说明可以把它写出,而且这样可使我们预先看到它的大致面貌。其实,电与磁的正确规律的最有用 的写法并不是我们现在的写法,而是包含所谓场方程 的写法,我们将在下一学年学习这些方程。但由于这些方程的数学符号形式特别而且新颖,所以我们用现在所知道的符号,而对于计算并不方便的形式写出定律。
电场 E 可表示为
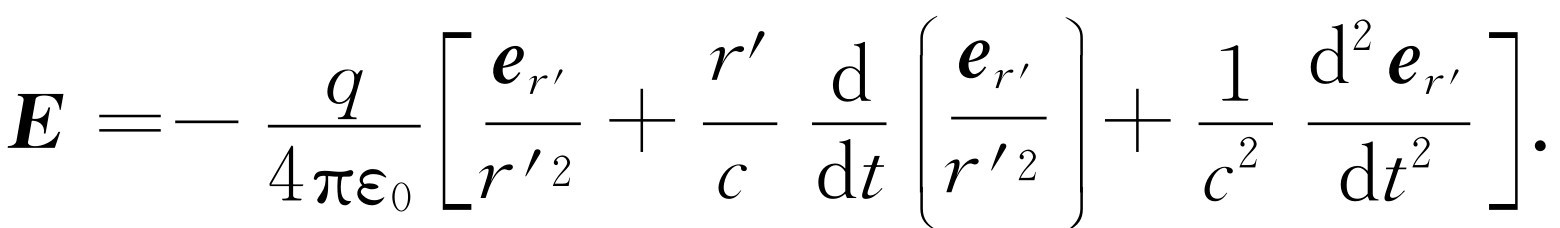 (28.3)
(28.3)
式中各项告诉我们一些什么?拿第一项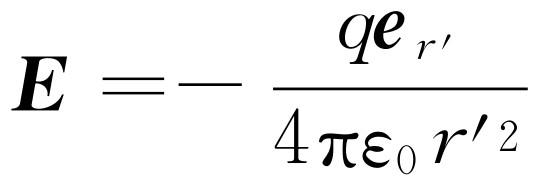 来说。这自然就是我们已经知道的库仑定律:q
是产生场的电荷,
来说。这自然就是我们已经知道的库仑定律:q
是产生场的电荷,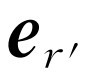 是从测量
E
的P
点出发的单位矢量,r
是从P
到q
的距离。但是,库仑定律是错误的。19世纪的发现揭示出任何作用不可能传播得比某个基本速度c
更快,这个速度我们现在称为光速。说第一项是库仑定律是不对的,这不仅因为我们不可能知道电荷现在
在哪里以及现在
的距离是多少,而且还因为在给定的地点和时间能够影响场的仅仅是电荷过去
的行为。过去多久
?时间的延迟,或者称为延迟时间
,是以速度c
从电荷到场点P
所需的时间,即延迟了r′
/c
。
是从测量
E
的P
点出发的单位矢量,r
是从P
到q
的距离。但是,库仑定律是错误的。19世纪的发现揭示出任何作用不可能传播得比某个基本速度c
更快,这个速度我们现在称为光速。说第一项是库仑定律是不对的,这不仅因为我们不可能知道电荷现在
在哪里以及现在
的距离是多少,而且还因为在给定的地点和时间能够影响场的仅仅是电荷过去
的行为。过去多久
?时间的延迟,或者称为延迟时间
,是以速度c
从电荷到场点P
所需的时间,即延迟了r′
/c
。
考虑到这个时间延迟,我们在r
上加一小撇,以表示现在到达P
点的信号在离开q
时离P
有
多远。暂且假定电荷带有光,而光只能以速度c
到达P
点。这样,当我们朝q
看时,当然看不见它现在在哪里,而只看见它若干时间以前曾在
哪里。在我们的公式中出现的是表
观的
方向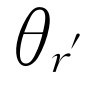 ——曾经所处的方向,即所谓延迟方向
,并处于延迟距离
r
′。这大概也是十分容易理解的,但这也是错误的。整个事情还要复杂得多。
——曾经所处的方向,即所谓延迟方向
,并处于延迟距离
r
′。这大概也是十分容易理解的,但这也是错误的。整个事情还要复杂得多。
还有另外几项。如果我们十分粗略地看,第二项就好像自然界试图考虑到推迟效应这一事实似的。它提示我们应计算延迟的库仑场,并附加一个改正项,即场的变化速率乘以所用的延迟时间。自然界似乎想用附加上变化速率乘以延迟时间这一项去推测现时的场要变成怎么样。但我们还没有完,还有第三项——在电荷方向上的单位矢量对时间的二次微商。现在公式总算 完成了,这就是来自一个任意运动电荷的电场的所有成分。
磁场可表示为
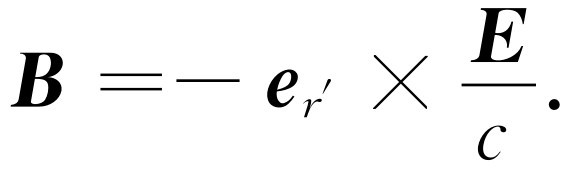 (28.4)
(28.4)
我们写下这些式子仅仅是为了显示自然界的美妙,或者在某种程度上,显示一下数学的威力。我们并不装作懂得怎么 可能在这么小的篇幅写下这么多的东西,但式(28.3)、(28.4)的确包含了发电机如何工作,光如何作用,以及所有电与磁现象的道理。当然,为了使描述完善起见,我们还必须知道所包含的物质行为的某些知识——即物质性质,这在式(28.3)中并未得到适当的表述。
为了完成我们对19世纪世界的描述,必须提及发生在那一世纪的,麦克斯韦在其中也做过许多工作的另一个巨大的综合,这就是热现象与力学现象的综合。我们将很快地学习到这方面的内容。
在20世纪必须补充说明一下的是发现牛顿的力学定律完全错了。必须引进量子力学去修正它。当物体尺度充分大时牛顿定律才近似有效。直到最近,这些量子力学定律才与电的定律结合起来而形成一组称为量子电动力学 的定律。另外,还发现了许多新的现象,其中首先是1898年 [1] 贝克勒尔发现的放射性现象——他只是在19世纪偷偷地把它带了进来。在发现这个放射性现象后,跟着就产生了关于原子核和新型力的知识,这些力不是引力,也不是电力,而是新的粒子间的另一种相互作用,这是至今仍未被阐明的一个课题。
对于那些知识渊博的咬文嚼字者(例如偶然读到此文的教授们),我们应补充一点:当我们说式(28.3)是电动力学知识的完整表述时,我们并不完全准确。有一个在19世纪末还没有完全解决的问题。当我们想计算来自所有电荷的场,包括来自此场所作用的电荷本身的场时 ,在寻找例如从电荷到该电荷本身的距离以及某一量除以该距离时遇到了麻烦,因为此距离为零。关于如何处理电场中由场所作用的电荷本身产生的这部分场的问题,至今还未解决。所以我们让它留着;既然对此难点尚无完善的解决办法,我们就尽可能地避开它。
§28-2 辐射
以上就是世界面貌的概括。现在我们用它来讨论称为辐射的一些现象。为了讨论这些现象,我们必须从式(28.3)中选出跟距离成反比而不是跟距离平方成反比的那一项来。当我们终于找到那一项时,发现它的形式是那么简单,以致只要把它作为远处运动电荷产生电场的“定律”,就完全可以用初等方法去研究光学和电动力学。我们将暂且把它作为已知的定律,到下一学年再详细地学习它。
在式(28.3)的诸项中,第一项显然与距离的平方成反比,第二项只是因延迟而作的修正,所以容易证明它们两者都随距离的反平方而变化。所有我们感兴趣的效应来自第三项,它倒并不十分复杂。这一项讲的是:看着电荷,并注意单位矢量的方向(我们可以把矢量的尾端投射到单位球的球面上)。当电荷来回运动时,单位矢量开始摆动,而单位矢量的加速度就是我们所要求的 。就这些。这样
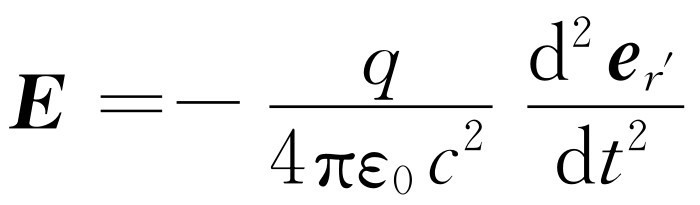 (28.5)
(28.5)
就是辐射定律的表述,因为当我们离得足够远时,它是唯一重要的项,这时场的变化与距离成反比(与距离平方成反比的部分已衰减为很小,以致我们对它们已不感兴趣)。
现在我们可以稍稍地深入一步来研究一下式(28.5),看看它的意义是什么。假定一电荷以任意方式运动,而我们在远处观察它。暂且想象在某种意义上它被“点亮”了(虽然我们想要解释的是光);我们把它想象为一个小的白点。于是我们将看到此白点在来回跑动。但是因为我们已经讲过的延迟的缘故,我们看不清楚它此刻
究竟在如何跑。重要的是它以前
怎么运动。单位矢量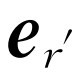 是指向电荷的表观位置的。显然,
是指向电荷的表观位置的。显然,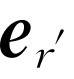 的尾端沿着稍稍弯曲的路线运动,因此它的加速度有两个分量。一个是横向分量,因为其尾端在上下运动;另一个是径向分量,因为它停留在球面上。容易论证后者要小得多,并且当r
很大时与r
的平方成反比。这很容易看出的,因为当我们想象把一给定的源移到很远很远时,
的尾端沿着稍稍弯曲的路线运动,因此它的加速度有两个分量。一个是横向分量,因为其尾端在上下运动;另一个是径向分量,因为它停留在球面上。容易论证后者要小得多,并且当r
很大时与r
的平方成反比。这很容易看出的,因为当我们想象把一给定的源移到很远很远时,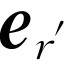 的摆动就显得很小很小,并与距离成反比,但加速度的径向分量比距离的倒数变化得更快。所以对实际目的来说,我们只要将运动投射在单位距离的平面上就行。于是我们得到下述规则:想象我们看着运动电荷,并且我们所看到的一切都是被延迟的——就像一位画家想把风景画在单位距离远的屏上一样。当然,真的画家并不考虑光以一定速率行进这一事实,而是画下他所见到的世界。我们想看看他的画将会是什么样子的。于是我们看到代表电荷的一个点在画面上运动,这个点的加速度与电场成正比。这就是我们所需要的一切。
的摆动就显得很小很小,并与距离成反比,但加速度的径向分量比距离的倒数变化得更快。所以对实际目的来说,我们只要将运动投射在单位距离的平面上就行。于是我们得到下述规则:想象我们看着运动电荷,并且我们所看到的一切都是被延迟的——就像一位画家想把风景画在单位距离远的屏上一样。当然,真的画家并不考虑光以一定速率行进这一事实,而是画下他所见到的世界。我们想看看他的画将会是什么样子的。于是我们看到代表电荷的一个点在画面上运动,这个点的加速度与电场成正比。这就是我们所需要的一切。
因而式(28.5)就是辐射的完整而正确的公式;甚至相对论效应也都包含在其中了。然而我们常常需要将它应用于电荷以比较慢的速度运动一段不大的距离这样更简单的情况。既然它们运动得较慢,它们就不会从始点移动太大的距离,所以延迟时间实际上不变。于是规律就更简单,因为延迟时间是固定的。因而我们想象电荷在实际上差不多不变的距离作很小的运动。在距离r
上的延迟是r
/c
。这样我们的规则变为如下:如果带电物体作很小的运动,并横向位移了距离x
(t
),则单位矢量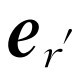 的角位移就是x
/r
,既然r
实际上不变,
的角位移就是x
/r
,既然r
实际上不变,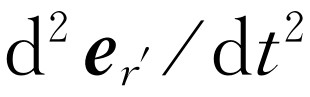 的x
分量就是x
本身在前一时刻的加速度
[2]
,最后我们得到所需的定律为
的x
分量就是x
本身在前一时刻的加速度
[2]
,最后我们得到所需的定律为
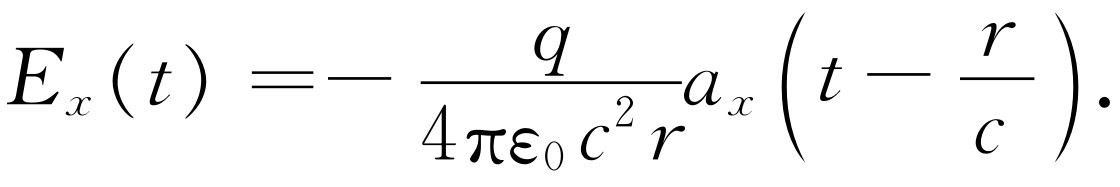 (28.6)
(28.6)
只有a x 的垂直于视线的分量是重要的。我们来看为什么是这样。显然,如果电荷笔直朝着我们运动或背向我们运动,此方向上的单位矢量根本就不会摆动,于是它没有加速度。所以只有横向运动是重要的,即我们所看到的投影在屏上的加速度是重要的。
§28-3 偶极辐射子
作为电磁辐射的基本“定律”,我们打算假定式(28.6)是正确的,也就是说,由一个在很远距离r 处作非相对论运动的加速电荷产生的电场近似取那个形式。此电场与距离r 成反比,与投影到“视平面”上的电荷的加速度成正比,这个加速度不是现在的加速度,而是前一时刻所具有的加速度,延迟的量是时间r /c 。在本章的其余部分我们将讨论这一定律,以使我们能更好地理解其物理意义,因为我们打算用它去理解光和无线电传播的所有现象,诸如反射、折射、干涉、衍射和散射等。这是主要的定律,而且是我们所要求的。我们写下式(28.3)的其余部分只是作为一个阶梯,使我们能够估计式(28.6)在哪里适用以及它是如何得出的。
下一学年我们将更深入地讨论式(28.3)。暂且我们当它是正确的,但不仅仅是在理论的基础上。我们可以设计许多实验来说明此定律的特征。为此,我们需要一个加速电荷。它应是单个电荷,但是如果我们使许多电荷一起作同样的运动,我们知道这时的场将是每个电荷单独产生的效果的总和,因而只要将它们加在一起就行了。作为一个例子,考虑两根与信号发生器相连接的导线,如图28-1所示。我们的想法是这样的:信号发生器产生一个电位差或电场,在某一瞬时它把电子从A拉出,推向B,经过极短时间以后,它又使过程反过来,把电子从B拉出而注回到A!所以可以说在这两根导线中的电荷一会儿在A线与B线上都向上加速,过一会儿在A线与B线上又都向下加速。我们之所以需要两根导线与一个发生器,只是因为那是做到这一点的一种方法。其净效果如同A和B是单根导线,只有一个电荷在其上下加速一样。一根长度比光在一个振动周期内传播的距离短得多的导线叫做电偶振子 。这样我们就有了应用定律的条件,此定律告诉我们此电荷产生一个电场,因而我们需要用仪器去探测电场,而这类仪器就是同一个东西——像A和B一样的一对导线!如果有电场作用在这样的装置上,电场将产生一个力把两根导线上的电子都拉上或拉下。此信号用接于A和B之间的整流器来探测,并用一根纤细导线将其输入一个放大器,信号在其中放大后,我们就能听到调制在无线电频率上的声频音调。当这一探头探到电场时,将会有一个响亮的声音从喇叭中发出,当没有电场激励它时,就不会有声音。
由于我们测量波所在的房间里还有其他一些东西,电场也将扰动这些东西上的电荷;电场使这些其他的电子上下运动,在这个过程中,电子也会对探头产生作用。所以为了使实验获得成功,必须把仪器放得相当靠近,这样,来自墙上和我们自己身上的影响——反射波——就比较小了。所以测出的现象的结果不会精确而完全地与式(28.6)相符,但将接近得足以使我们能够验证定律。
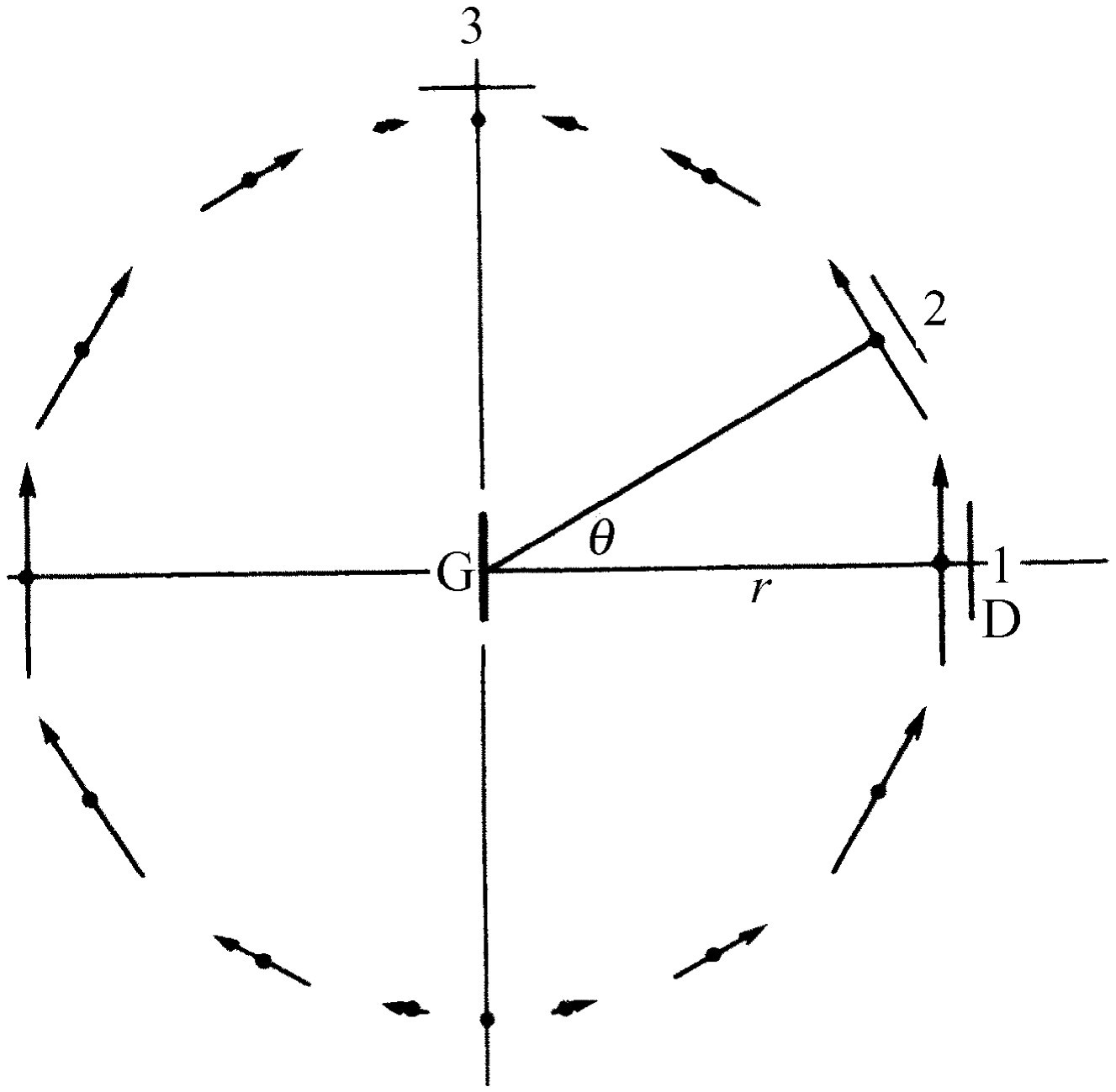
现在我们接上发生器来听音频信号。当处于位置1的探测器D与发生器G平行时(图28-2),我们发现一个强电场。在环绕G的轴的其他任何方位角上我们也发现同样大小的场,因为它没有方向性效应。另一方面,当探测器在位置3时场为零。这是对的,因为我们的公式表明场是由电荷的加速度对于视线的垂直投影 引起的。当我们向下看G时,电荷朝着D或背离D运动,所以没有效应。因而它验证了第一个规则,即当电荷直接朝我们的方向运动时没有效应。其次,公式表明电场应垂直于r ,并在G和r 组成的平面内;所以如果我们把D放在1处而转过90°,应得不到信号。这正是我们所发现的,电场确实是竖直的,而不是水平的。当我们把D移到中间某角度时,我们看到最强的信号出现在D处如图所示的取向上,因为虽然G是竖直的,但它并不只简单地产生与G本身平行的场——起作用的是加速度在垂直于视线方向上的投影 。在2处的信号比1处的弱,因为此处投影较小。
§28-4 干涉
接下来,我们试验一下当有两个源相距几厘米并排着时将发生什么现象(图28-3)。它的规律是:当两个源与同一发生器相联,其上电子以同一方式一起上下运动时,它们在1处的效应应当相加,因而总电场是两个电场的和,即为原来强度的两倍。
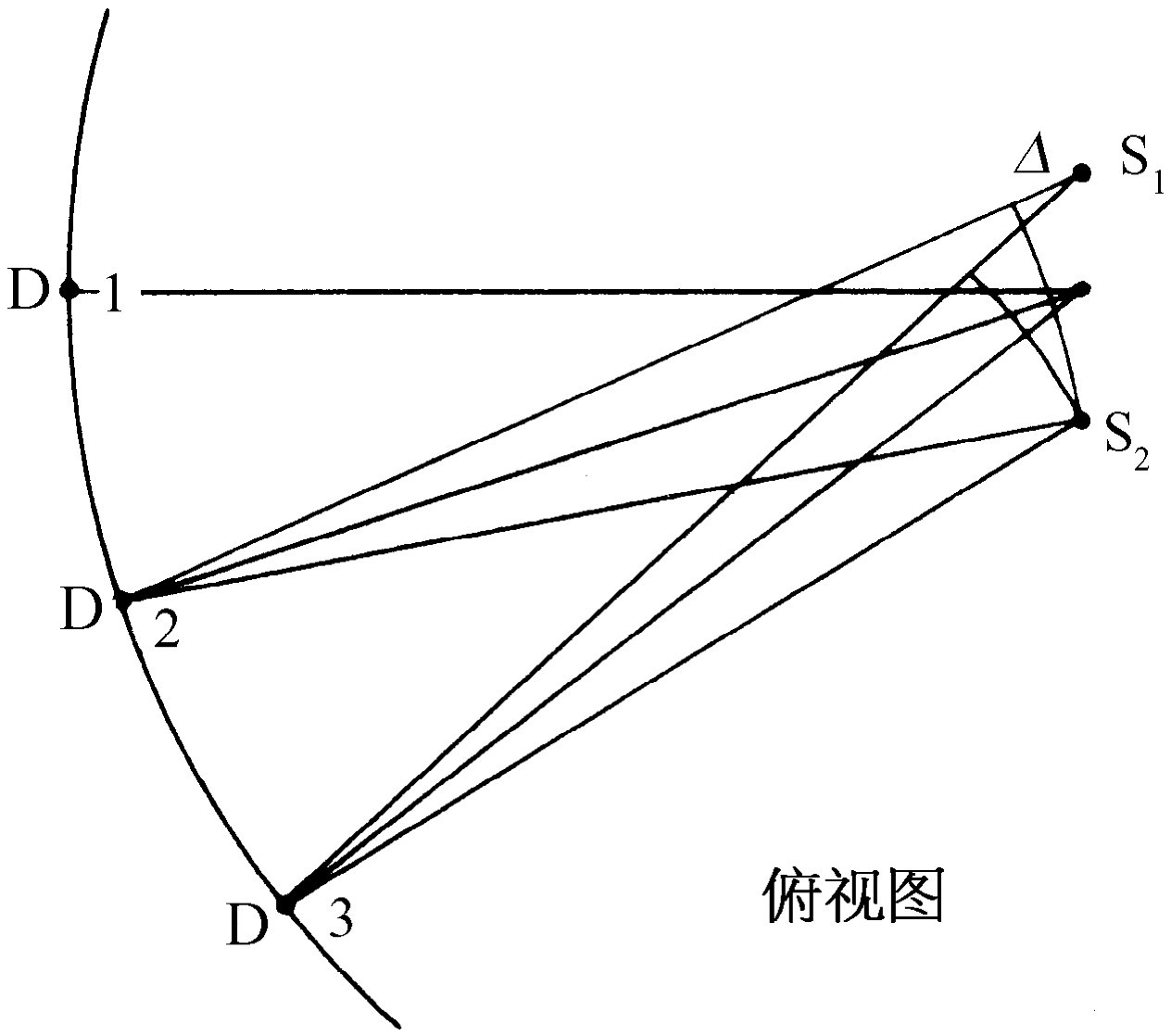
图28-3 两个源的干涉的示意图
现在出现了一个有趣的可能性。假如使S1 和S2 中的电荷都上下加速运动,但让S2 延迟一些时间,使它们的相位差180°。这样,在任一瞬时,若S1 产生的场沿某一方向,S2 产生的场就沿相反方向,于是我们在1处就得到零 效应。振荡的相位借助于将信号输送给S2 的一个管道可巧妙地加以调节。改变此管道的长度,我们可以改变信号到达S2 的时间,于是就改变了振荡的相位。调节这一长度,我们确实能够找到没有什么信号的地方,尽管S1 和S2 中的电子都在运动着!它们的电子都在运动这一事实是可以验证的,因为如果将一个源切断,就可观察到另一个源是在运动。所以,只要调节得恰当,两个源在一起能够产生零 效应。
证明两个场的叠加是矢量 叠加这一点是十分有趣的。我们刚才已验证了源的上下运动,现在我们来验证两个运动方向不平行的源。首先,让S1 与S2 恢复为同相;这就是说,它们又一起运动了。但现在把S1 转过90°,如图28-4所示。那么在1处我们应得两个效应之和,一为竖直的,另一为水平的。电场为此两个同相信号——它们同时达到最强又一起通过零——的矢量和;总的场应为在45°方向上的信号R 。如果我们转动D以听到最大声音,它应在约45°方位,而非竖直方向。若我们将D转至与该方向垂直的方位,应得到零,那是很容易测量的。诚然,我们确实观察到这样的现象!
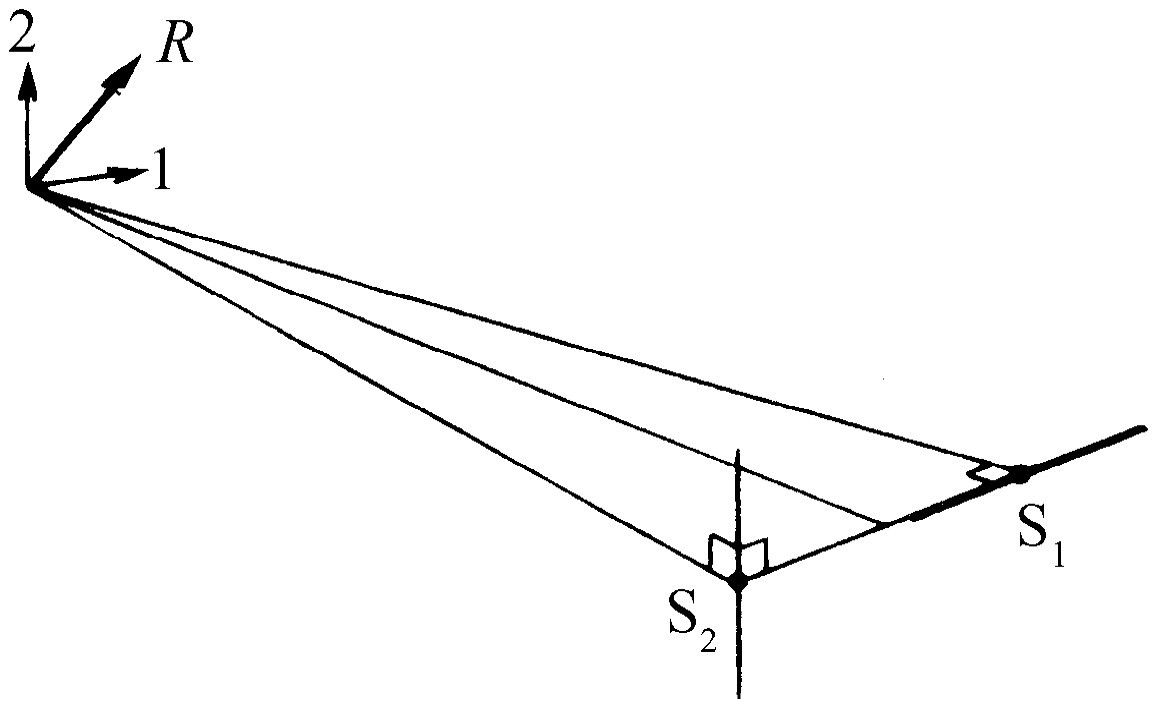
图28-4 两个源叠加时的矢量特征示意图
那么,推迟效应在哪里?我们如何演示信号被推迟了?我们可以利用大量装置来测量到达的时间,但另有一个非常简单的方法。再参看图28-3,假定S1 与S2 同相。它们一起振动,并在1处产生相等的电场。但是如果我们把D移到靠S2 较近,而离S1 较远的2处,那么,根据加速度应延迟一个r /c 值的原理,如果两个延迟量不相等,两个信号就不再同相了。于是就能找到一个位置,使从D到S1 和到S2 的距离相差某一个量Δ ,在此位置上没有净信号。那就是说,距离Δ 即为光在发生器振荡半周期中所通过的距离。还可以把D再移过去一些,找到相差为一个整周的点;那就是说,信号从第一根天线S1 到达3处的延迟时间比第二根天线S2 到达3处的延迟时间正好长了电流振荡一次所需的时间,因此在3处产生的两个电场又同相了。在3处信号又是强的。
这样就完成了我们对式(28.6)的一些重要特征的实验证明的讨论。当然我们没有真正验证电场强度按1/r 变化这一点,也没有验证磁场伴随电场行进这一点。要做到这几点需要相当复杂的技术,而且几乎不会增加我们对该点的理解。总之,我们已验证了那些对我们以后应用最重要的特征,下一学年我们将回过来再研究电磁波的另外一些性质。

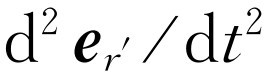 的
的