第35章 色视觉
§35-1 人眼
颜色的现象部分地依赖于物理世界。我们讨论肥皂膜等等的颜色时,认为它们是由干涉所产生。但颜色当然也取决于眼睛,以及在眼睛后面大脑中所发生的过程。物理学描述进入眼睛的光的特性,但在进入以后,我们的感觉是光化学神经过程和心理反应的结果。
有许多有趣的现象往往和视觉联系在一起,这些现象是物理现象与生理过程的一种混合,而要完全理解各种自然现象,像我们所看到的那样,则必定超出了通常意义下的物理学范围。我们不需要为离开正题去讨论其他领域的内容提出辩解,因为各个领域的划分,正如我们已经强调的,仅仅是由于人们的方便,而且也是一种很不自然的事。自然界对我们的这种划分并不感兴趣,而许多有趣的现象就在各个领域之间的沟壑上架起了一座座桥梁。
在第3章中我们已经一般地讨论过物理学和其他科学的关系,但现在我们将稍微详细地研究一下一个特殊的领域,在这个领域里物理学和其他科学是非常紧密地互相联系着的。这个领域就是视觉 。我们特别要讨论色视觉 。在这一章中将讨论视觉的生理方面,包括人和其他动物的。
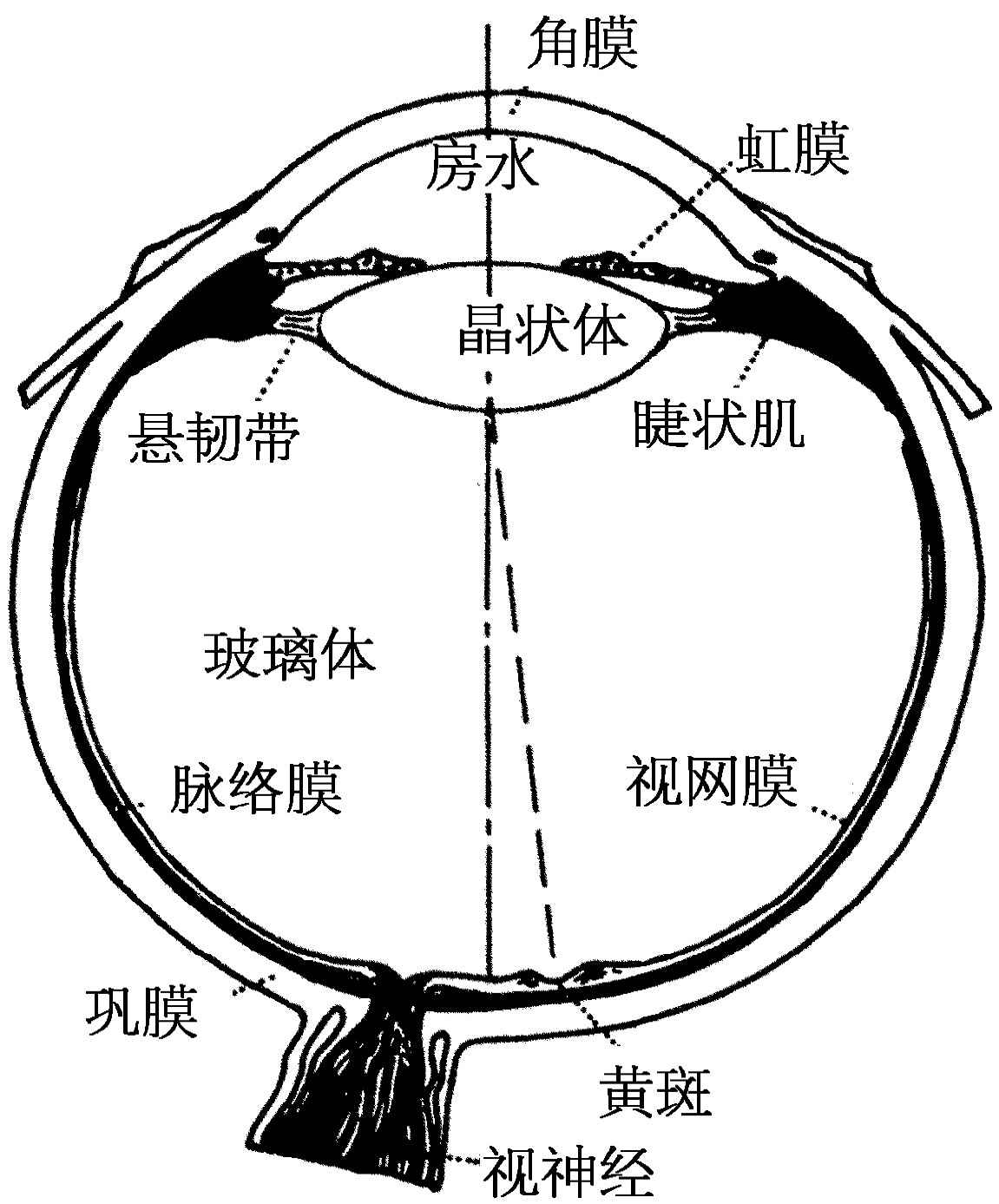
一切都是从眼睛开始;所以,为了要理解我们所看到的是一些什么现象,就需要某些有关眼睛的知识。在下一章中,我们将比较详细地讨论眼睛的各个部分是怎样工作的,以及它们和神经系统怎样相互连结。但在目前,我们只想简单地描述一下眼睛是怎样起作用的(图35-1)。
光通过角膜 进入眼睛。我们已经讨论过它如何被弯曲而成像在眼睛背后叫做视网膜 的薄膜上,从而视网膜的不同部分接收到从外界视场不同部分射来的光。视网膜不是绝对均匀的:在我们的视场中心有一个地方,即一个斑点,当我们试图非常仔细地观察物体时就使用这个斑点,在这里我们有最大的视觉敏锐度,这个斑点叫做中央凹 或黄斑 。眼睛的旁边部分,正像我们注视物体时所获得的经验立刻促使我们意识到的那样,对于看清楚物体上的细节不像眼睛中央部分来得有效。视网膜上还有另一个斑点,输送各种信息的神经就是从这里延伸出去的,那是盲点。这里没有视网膜的敏感部分,并且可以这样来证明:如果我们闭上比如说左眼,用右眼对直观察某一物体,然后把一个手指或者一个小的物体慢慢地从视场中央向外移开,那么在某个地方它会突然消失不见。关于这个事实,我们所知道的唯一的实际用处就是,某个生理学家因为向法国国王指出了这一点而成了宫廷中的宠臣,在国王和他的大臣们举行的令人厌倦的例行朝会上,国王可以用“砍掉他们的头”,即盯着一个头而看着另一个头消失来自我消遣。
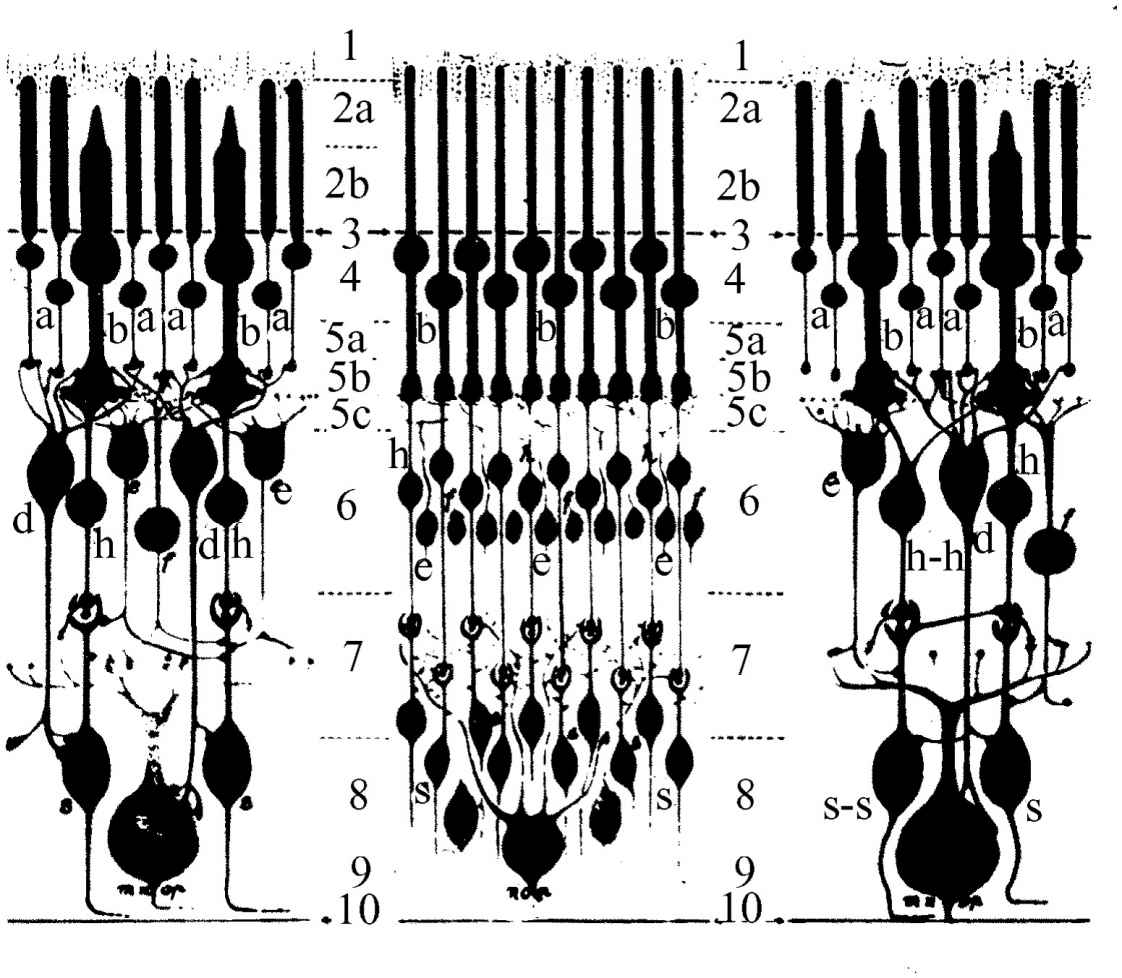
图35-2以比较简单的形式显示视网膜内部的放大图像。视网膜的不同部分具有不同的结构。密集在视网膜外周的那些感光细胞叫做视杆细胞 ,而靠近中央凹处,除了这些视杆细胞外,我们还看到视锥细胞 。关于这些细胞的结构,我们将放到以后去讲。越接近中央凹处视锥细胞的数目越多,而在中央凹处,事实上别无他物,只有视锥细胞,它们靠拢得非常紧密,以致这些视锥细胞比任何其他地方都细小得多。所以我们必须意识到,我们是使用位于视场正中的视锥细胞来观看的,但是在外围地方,则有另一种细胞,即视杆细胞。现在有趣的是,视网膜中每一个对于光敏感的细胞不是通过一根纤维直接与视神经相连结,而是与许多细胞交错连结联系在一起的。此外,还有好多种细胞:有向视神经输送信息的细胞,也有主要是“水平地”相互连结在一起的其他细胞。实质上有四种细胞,但是我们现在不预备深入讨论这些细节。我们要强调的主要一点就是光信号已被“考虑”过了。这就是说,来自各种细胞的信息不是一点一点地直接通往大脑,而是在视网膜中,把来自几个视觉接收器的信息组合起来,将一定数量的信息整理汇编。这里重要的是应理解到,有些大脑功能现象是在眼睛本身中发生的。
§35-2 颜色依赖于光的强度
最令人惊奇的视觉现象之一是眼睛对黑暗的适应性。假如我们从明亮的房间走进黑暗中去,开始有一段时间什么也看不清楚,但是渐渐地物体变得越来越清晰,终于在我们以前看不到东西的地方能够看到一些东西。如果光的强度非常弱,我们看到的东西是没有颜色 的。我们知道,这种适应黑暗的视觉几乎应完全归功于视杆细胞,而适应亮光的视觉则应归功于视锥细胞。作为这方面的一个结果,有好些现象我们可以很容易把它们解释为由于功能的这种转换,即视锥细胞和视杆细胞的共同作用转换为只有视杆细胞作用所引起。
在许多情形中,如果光的强度比较强,我们就能看到颜色,而且还会发现这些东西极其美丽。一个例子是,通过望远镜观察微弱的星云时,我们几乎总是看到它的“黑白”像,但是威尔逊山天文台帕洛玛天文台的米勒先生却耐心地给某些星云拍摄了彩色图像。从来没有人曾经真正用肉眼看到过这些颜色,然而这些颜色并不是人为的颜色,只是光的强度还不足以使我们眼睛中的视锥细胞能够看到它们。这些星云中比较壮丽的有环状星云和巨蟹座星云。前者呈现美丽的蓝色内核,并带有亮红色的外晕,后者呈现蓝色的云雾,并带有明亮橘红色的细丝渗入其中。
在亮光中,视杆细胞的灵敏度显然非常低,但在黑暗中,随着时间的流逝,它们逐渐获得了能够看到光的本领。人们所能适应的光的强度变化超过了一百万比一的范围。大自然并不是只用一种细胞来完成所有这一切,而是把她的职能从看到亮光的细胞,即看到颜色的细胞,也就是视锥细胞转移到看到低光强的细胞,即适应黑暗的细胞,也就是视杆细胞。在这一转移所产生的有趣的结果之中,首先是没有颜色,其次是颜色不同的物体其相对亮度也不同。这是因为视杆细胞对蓝色的感光比视锥细胞要好,而视锥细胞能看到的光的颜色如深红色,视杆细胞却绝对不可能看到。所以对视杆细胞来说,红光是黑色的。因此,两张颜色纸,比如说一蓝一红的,在明亮的光线下,红色甚至可能比蓝色更亮一些,可是在黑暗中却看上去完全相反。这是一个非常惊人的效应。如果我们在黑暗中能找到一本杂志或者有颜色的某种东西,在我们能确切知道它们是什么颜色之前,先判断一下哪些是较亮,哪些是较暗的区域,然后把杂志带到亮光中去,那么,我们就会看到这种在最亮和不是最亮的颜色之间发生明显的转移。这种现象叫做普尔基涅效应 。
在图35-3中,虚线表示眼睛在黑暗中的灵敏度,也就是它用的是视杆细胞;实线表示在亮光中的灵敏度。我们看到,视杆细胞的峰值灵敏度在绿色区域,而视锥细胞的峰值灵敏度更多的在黄色区域。如果有一页红纸(红光波长大约为650 nm),在明亮的光照下,我们能够看到它,但在黑暗中就几乎看不见它。
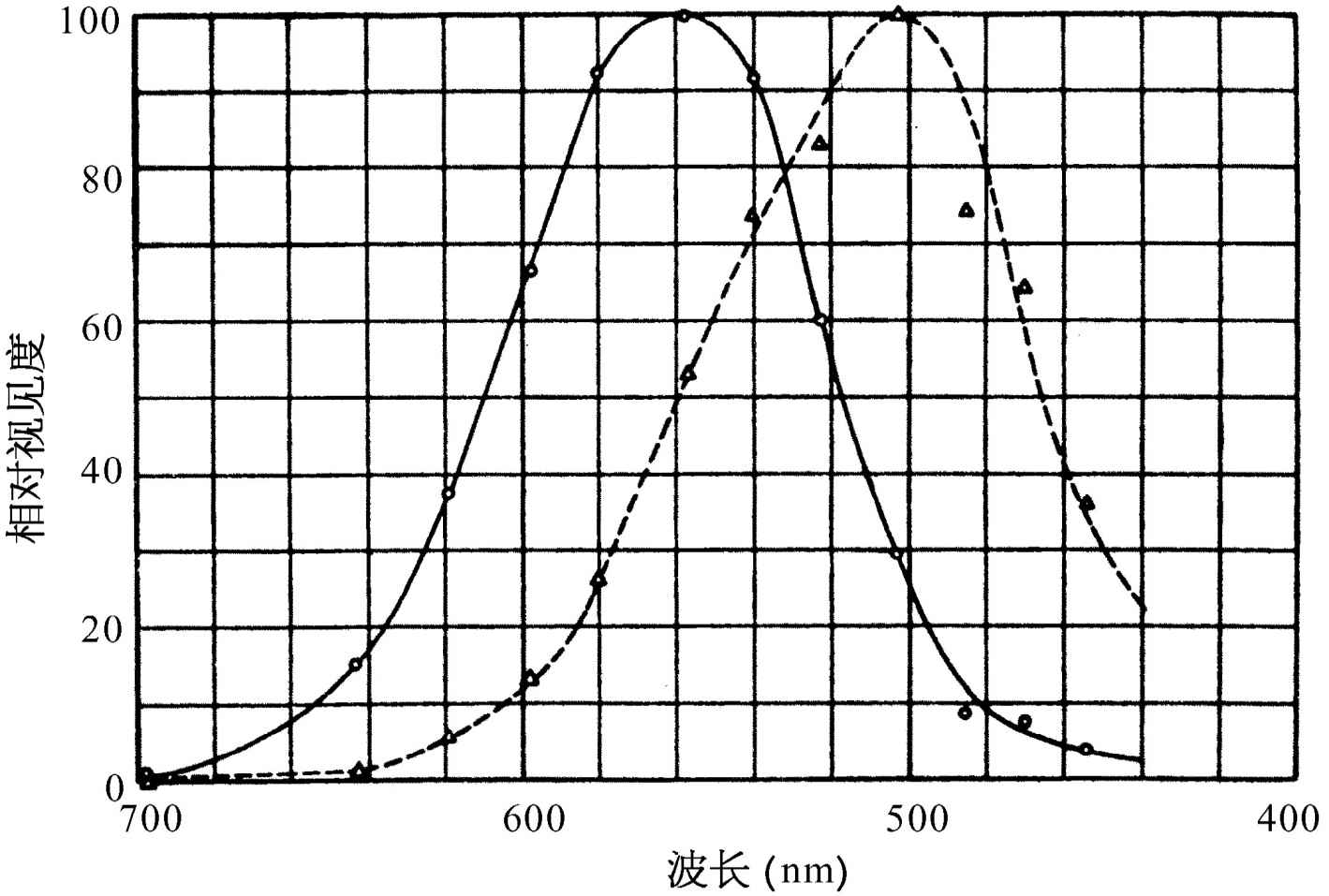
图35-3 眼睛的光谱灵敏度。虚线——视杆细胞;实线——视锥细胞
在黑暗中由视杆细胞来承担任务以及在中央凹处没有视杆细胞这一事实的另一效应是,当我们在黑暗中直接观察某一物体时,我们的视觉不如向一边看时来得敏锐。对弱的星或星云,当我们稍微偏向一边注视时,有时会比直接对着它注视更为清楚,因为在中央凹处的中心没有灵敏的视杆细胞。
越往视场旁边视锥细胞的数目越是减少这个事实的另一有趣的效应是,当物体往一边移去时,即使在明亮的亮光中颜色也会消失。试验它的方法是朝着某一特定不变的方向看去,请一位朋友拿着一些有颜色的卡片从一边走进来,在这些卡片到你面前之前先试试看判定它们是什么颜色。人们发现,在他能够看见这些卡片在哪里之后很久,才能确定它们的颜色。在做这项试验时,建议最好从与盲点相反的一边走进来,因为不然的话,就会被搞糊涂,一会儿几乎看见了颜色,一会儿(当经过盲点时)什么也看不见,然后又重新看到了颜色。
另一个有趣的现象是视网膜的外围对于运动非常敏感。虽然从我们的眼角去看时不可能看得很清楚,但是如果有一个小虫在爬动,而且我们原来未料想到那里有某一种东西在移动,我们就会立即对它很敏感。我们都会“紧张起来”去寻找正在爬到视场边上的那个东西。
§35-3 色感觉的测量
现在我们转到视锥细胞视觉,即亮光中的视觉上来,所涉及的问题是视锥细胞视觉最主要的特征是什么,那就是颜色。我们知道,白光可以用棱镜分解成具有各种波长的整个光谱,而光谱的不同波长在我们就看到不同的颜色;当然这就是我们能看到的各种颜色。任何光源都可用光栅或棱镜加以分析,并且可以确定它的光谱分布,也就是每一波长的“份量”。某一种光可以包含有大量的颜色,相当数量的红色,以及一点点黄色,等等。这在物理的意义上是非常精确的。但问题是它看起来是什么颜色 ?很明显,各种不同的颜色在一定程度上依赖于光的光谱分布,但是问题在于要去找出产生各种不同感觉的是光谱分布 的哪些特征。例如,我们必须怎样去做才能获得绿色?大家知道,我们可以简单地从光谱中取绿色的那部分。但这是否是得到绿色,橙色或任何其他一种颜色的唯一 方法呢?
能够产生同样表观视觉效应的光谱分布是否不止一种呢?答案是完全肯定 的。视觉效应的数目非常有限,而且事实上正如我们下面就要看到的那样,它们正好是一个三维流形。但是对于不同光源发出的光,我们所能画出的不同曲线数目是无限的。现在我们要讨论的问题是,在什么情况下光谱的不同分布对于眼睛会显示出完全相同的颜色?
在判断颜色方面,一个最有力的心理-物理技术是把眼睛用作衡消仪器 。这就是说,我们并不试图去定义究竟是什么造成绿色的感觉,或者去测量在什么情况下我们得到绿色的感觉,因为很清楚要这样去做是非常复杂的。我们代之以研究在什么条件下两个刺激是不可区分的 。这样,我们就无需判定在不同情况下两个人是不是会得到同样的感觉,而只去判定如果两种感觉对于一个人是相同的话,对于另一个人是否也相同。我们并不需要去判定,当一个人看到某个绿色的物体时,在他内心深处引起的感觉和另外某个人在他看到某个绿色的物体时是否也相同,关于这一点我们什么也不知道。
为了说明这种可能性,我们可以用一组四盏各带有滤色片的投影灯,它们的亮度可以在一个较宽的范围内连续调节:一盏灯带有红色滤色片,在屏幕上映出一个红色光斑。另一盏灯带有绿色滤色片,在屏幕上映出一个绿色光斑。第三盏灯带有蓝色滤色片。第四盏灯在屏幕上映出一个白色圆环形光圈,它的中央有一个黑斑。现在如果我们开亮红光,并且靠近它加上一些绿光,我们看到,在两种光重叠的区域里所产生的并不是我们所说的那种绿色带红的感觉,而是一种新的颜色,在我们这个特例中是黄色。改变红光和绿光的比例,我们可以得出各种深浅不同的橙色,等等。如果我们已把它配成某一种黄色,那么我们不通过这两种颜色的混合而是把另外的一些颜色混合起来也能得到同样的黄色,也许用黄色滤色片和白光,或者诸如此类的东西混合起来,可以得到同样的感觉。换句话说,可以用不止一种方法把通过各种滤色片的光混合起来以形成各种颜色。
我们刚才发现的这种情况可以用解析方法表述如下。例如,一种特定的黄色可以用某一符号Y 表示,它是某一数量的红色滤色光(R )和绿色滤色光(G )的“和”。在用两个数字比如r 和g 描写(R )和(G )有多亮,我们可以写下这种黄色的一个公式
Y =rR +gG .(35.1)
现在的问题在于,是否通过把两种或三种固定的不同颜色相加在一起,就能做成所有 各种不同的颜色?我们来看一看,在这方面可以得到什么结论。只把红色和绿色混合起来,肯定是不能得到所有各种不同的颜色的,因为比如说在这样的混合物中决不会出现蓝色。然而在加进一点点蓝色后,可以使所有三个斑点重叠的中央区域看来像是一种十分美妙的白色。把这三种不同的颜色混合起来,并且观察这个中央区域,我们会发现,通过改变颜色的比例,可以在这个区域中得到范围相当宽广的不同颜色,所以所有的 颜色可以用这三种色光的混合来做成并非不可能。我们要讨论一下这在多大程度上是真实的。事实上这一点基本上是正确的,不久我们将看到怎样把这个命题定义得更加完善一些。
为了说明我们的观点,在屏幕上移动各个光斑,使它们彼此都落在其他光斑的上面,然后试着去配制出一种特殊的颜色使它落在第四只灯映出的圆环中央并使内外颜色相同。从第四盏灯射出的以前我们曾经认为它是“白色”的光现在却呈现出淡黄色。我们可以借助于尝试法尽可能适当地调节红色、绿色和蓝色以配制那种颜色,并且发现,我们能够相当接近于这种特殊浓淡的“奶油”色。所以不难相信,我们能够配制出所有的颜色。我们不久就要试制黄色,但是在这以前,必须指出:有一种颜色可能很难制成。教颜色这门课程的人都只制成所有“鲜明的”颜色,但从来没有制成过棕色 ,而且人们很难回忆起曾经看见过棕色的光。事实上,为了增加任何舞台效果,这种光从来没有被使用过,人们也从来没有看到使用棕色光的聚光灯。所以我们想,或许不可能制成棕色光。为了弄清楚是否可以制成棕色光,我们指出,棕色光仅仅是这样一种光,如果没有背景的衬托,我们就不习惯于看它。事实上,我们能够把一些红光和黄光混合起来而制成棕色光。为了证明我们看到的是棕色光,只要增加圆环背景的亮度,相对于这个背景,我们看到的正是这种光,它就是我们所说的棕色!棕色在靠近比较明亮的背景时,总是一种深暗的颜色。棕色的特征很容易改变。比方说,如果我们从中取出一些绿色,就得到略带红的棕色,这显然是一种巧克力似的红棕色。如果加进更多的绿色,那么我们就相应得到那种令人讨厌的所有的军队制服都由它染成的颜色。但是来自这种颜色的光本身并不那样令人讨厌,它是略带黄的绿色,但是在明亮的背景的衬托下就显得非常可憎了。
现在我们在第四盏灯的前面放置一片黄色滤色片,并试图配制出这种颜色(光的强度当然必须限于各灯的范围之内,我们不可能去配制太亮的光色,因为我们的灯没有足够的功率)。然而我们能够 配制出黄色,为此只要把绿色和红色混合起来,甚至加上一点点蓝色,使它更加完美。或许我们已经相信,在恰当的条件下,能够完美地配制出任何给定的颜色。
现在我们来讨论颜色混合的定律。第一,我们曾发现不同光谱分布的光能够产生同样的颜色;其次,我们曾看到“任何”颜色可以通过把三种特殊的颜色:红、蓝和绿加在一起而配制出来。混合的颜色最有趣的特点是:设有某一种光,我们把它叫做X ,又设从眼睛看来它和Y 没有什么区别(它可以是一种与Y 不同的光谱分布,但它看起来 与Y 是不可区别的),那么我们称这些颜色是“相等”的,这是从这个意义上来说,即眼睛看到它们是相等的,并且可以写成
X =Y .(35.2)
颜色的主要定律之一是:如果两个光谱分布是不可区别的,我们给每一个加上某一种光,比如说Z (如果我们写成X +Z ,就意味着把这两种光照射在同一个斑点上),然后再取Y 并加上同样数量的另一种光Z ,那么这些新的混合物也是不可区别的
X +Z =Y +Z .(35.3)
我们刚才已经配制出黄色,如果现在把粉红色的光照射到全部物体上,它们仍然能够匹配。所以对已经匹配的光,加上任何其他的光,留下的仍然是相匹配的光。换句话说,我们可以把所有这些颜色现象总结起来:两种色光在相同情况下彼此靠近观察时,如果一经匹配,那么这种匹配将继续保持下去,而且在任何其他的颜色混合情形中,一种光可以用另一种光来代替。事实上,这证明了一个非常重要和有趣的情况,即色光的这种匹配不依赖于眼睛在观察那个时刻的特性:我们知道,如果我们长时间地注视一个明亮的红色表面或者明亮的红光,然后去看一张白纸,那么它看上去略带绿色,而且其他颜色也会因我们长时间地注视着明亮的红色而走样。如果我们现在把两种颜色,例如黄色相匹配,我们注视它们,然后长时间地去注视一个明亮的红色表面,然后再回过来看黄色,这时它看上去不是黄色的了。我不知道它看上去是什么颜色,但看来不会是黄色。虽然如此,这些黄色看上去仍然是匹配的 ,因此,由于眼睛能适应光的不同强度,颜色的匹配仍然发生作用,除非一个明显的例外,那就是当我们进入一个领域,在那里光的强度如此之弱,以致我们必须从视锥细胞转移到视杆细胞的时候,这时原来相匹配的颜色不是相匹配的了,因为我们运用了不同的系统。
颜色混合的第二个原理是:任何一种颜色都可以用三种颜色组成 ,在我们的情况中,就是红、绿和蓝三种色光。适当地把这三种颜色混合在一起,我们就能够配制出任何一种颜色,正像我们在前面两个例子中所表明的那样。此外,这些定律在数学上也非常有趣。对那些对于事物的数学感兴趣的人来说,情况是这样:假设我们取红、绿和蓝三种颜色,用A 、B 和C 来标记,并且把它们叫作原色 。于是任何一种颜色都可以由这三种颜色的一定数量配成:比如由颜色A 的数量a ,颜色B 的数量b 和颜色C 的数量c 配成X
X =aA +bB +cC .(35.4)
现在假设另一种颜色Y 由同样这三种颜色配制成
Y =a ′A +b ′B +c ′C .(35.5)
于是我们发现这两种光的混合物(这是我们在前面已经提到过的那些定律的结论之一)可以通过取X 和Y 的分量之和来求得
Z =X +Y =(a +a ′)A +(b +b ′)B +(c +c ′)C .(35.6)
这正好像数学中的矢量加法,其中(a ,b ,c )是一个矢量的分量,而(a′ ,b′ ,c ′)是另一矢量的分量,这时新的光Z 就是这些矢量的“和”。这个问题一直在引起物理学家和数学家们的注意。事实上,薛定谔曾经写过一篇有关色视觉的精彩论文,他在这篇论文中发展了这个可用于颜色混合的矢量分析理论。
现在的问题是,哪些可正确地用作原色?就光的混合来说,是没有正确的原色这类东西的。对于实用的目的,可能有三种颜色在得到比较多的混合色方面比其他颜色更为有用,但是我们现在不讨论这个问题。无论哪三种不同的颜色 [1] ,总能用正确的比例混合起来以产生无论哪种颜色。我们是不是能够证明这一奇妙的事实呢?若我们在投影灯中改用红色、蓝色和黄色来代替红色、绿色和蓝色。我们是否能用红色、蓝色和黄色配制成比如说绿色呢?
以各种比例把这三种颜色混合起来,我们得到范围相当大的一系列不同颜色,它们几乎遍及整个光谱。但是事实上,经过大量的尝试和失败,我们发现没有什么东西曾经看上去有点像绿色。问题在于我们是否能配制出绿色?回答是肯定的。那么如何配制呢?把一些红色光投射到所要配制的绿色上 ,我们就能用黄色和蓝色的某一混合色来与之相匹配!就这样,我们确实把它们匹配了,只是除去一点,那就是我们不得不欺骗自己一下,把红色放到另一边去。但是既然我们掌握了某种数学技巧,那就能理解到我们实际上所证明的并不是说X 总能从比如红色、蓝色和黄色配制,而是在把红色放在另一边之后,我们发现红色加上X 可以从蓝色和黄色中配制出来。把它放在等式的另一边,这可以解释为它是一个负的数量 ,所以如果我们允许像式(35.4)那样的等式中的系数既可以是正的也可以是负的,以及把负的数量解释为把它加到另一边 ,那么任何颜色都可以用任何三种颜色来配制,因而并没有像“这种”基本的原色这样的东西。
我们可以问,是不是有三种颜色,它们对于所有混合只有正的数量。回答是否定的。每一组三原色都对某些颜色要求负的数量,因而也就没有用以定义一种原色的唯一方法。在初等教材中,它们被说成是红色、绿色和蓝色,但那只是因为用这些原色对有些组合无需用负号即可得到较宽 的颜色范围而已。
§35-4 色品图
我们现在从数学的层面上作为一个几何学的命题来讨论颜色的组合。假如任何一种颜色能用等式(35.4)来表示,那么我们可以把它当作一个空间矢量来作图,沿着三根坐标轴画出a 、b 和c 的数值,于是一种颜色就是一个点。如果另一种颜色是a′ 、b′ 、c′ ,那么这种颜色就处在图中别的什么地方。我们知道,这两者之和就是把它们作为矢量相加而得到的颜色。我们可以把这个图解简化一下,并且通过如下的观察把所有东西表示在一个平面上:如果我们有某种颜色的光,而且仅仅把a 、b 和c 都加倍,也就是说,使它们都以同样的比例增强,那么它还是同一种颜色,只是更亮了一些。所以如果我们约定把所有东西都化为同样的光强 ,那么我们就能把所有东西都投影到一个平面上,这在图35-4中就已这样做了。由此可知,由给定的两种颜色以某一比例混合而成的任何颜色,将处在联结这两点的直线上某一地方。例如,50比50的混合色将处在它们之间的中点,一种色的1/4和另一种色的3/4将出现在从一点到另一点的1/4处,依此类推。如果我们以蓝色、绿色和红色作为原色,那么我们看到所有能用正的系数配制而成的颜色都处在虚线三角形之内,这几乎包含了所有我们能够看到的颜色,因为这些颜色都包围在以曲线为边界的钟形面积之中。这个面积是从哪里来的呢?有人曾经把所有我们能够看到的颜色与三种特殊颜色非常仔细地比较过。但是我们不必核对所能看见的所有颜色 ,而只要核对纯光谱色,即光谱线。任何一种光都可以认为是各种纯光谱色的各种正的数量之和——所谓纯是从物理观点来说的。一个给定的光包含有一定数量的红、黄、蓝等等这些光谱色。所以如果我们知道了要获得每一种纯成分需要用多少所选定的每一种三原色,那么就能算出要配制我们所给定的颜色每一种需要多少。所以,如果对任意给定的三原色,我们找出了所有光谱色的色系数 ,那么我们就能制订出整个的颜色混合表。
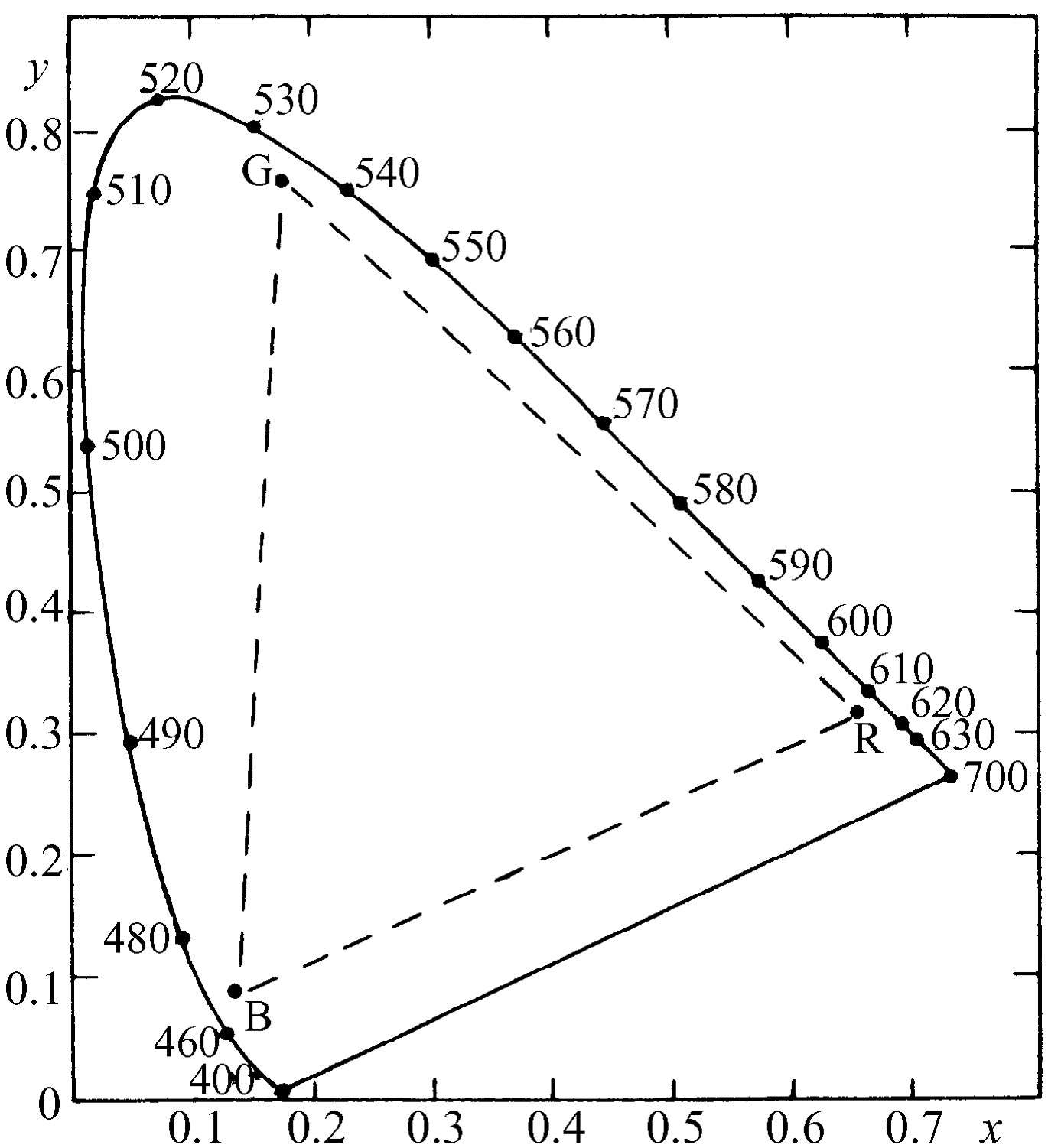
图35-4 标准色品图
把三种光混合起来这类实验的结果的一个例子如图35-5所示。这个图表明,要用红、绿、蓝三种不同的特殊原色配制出每一种光谱色时每一种的数量需要多少。红色在光谱的左端,黄色次之,依此类推,一直到蓝色。但应注意到,有些地方必须用负的符号。只是从这样一些数据才可能在一张其x 和y 坐标和所用各原色的数量有关的图上确定所有颜色的位置。这是找出两条弯曲边界线的方法。它是纯光谱色的轨迹。任何其他颜色当然都可通过光谱线的相加得到,因而我们发现,把曲线的一个部分和另一部分联结起来所能产生的任何颜色都是自然界中可以得到的一种颜色。图中的直线把光谱中紫色的最外一端和红色的最外一端联系起来。这是紫红色的轨迹。在边界之内是那些可以用各种光配制的颜色,而在它之外是不能用光配制的颜色,这些颜色从来没有人看到过(除非在余像中可能看到)。
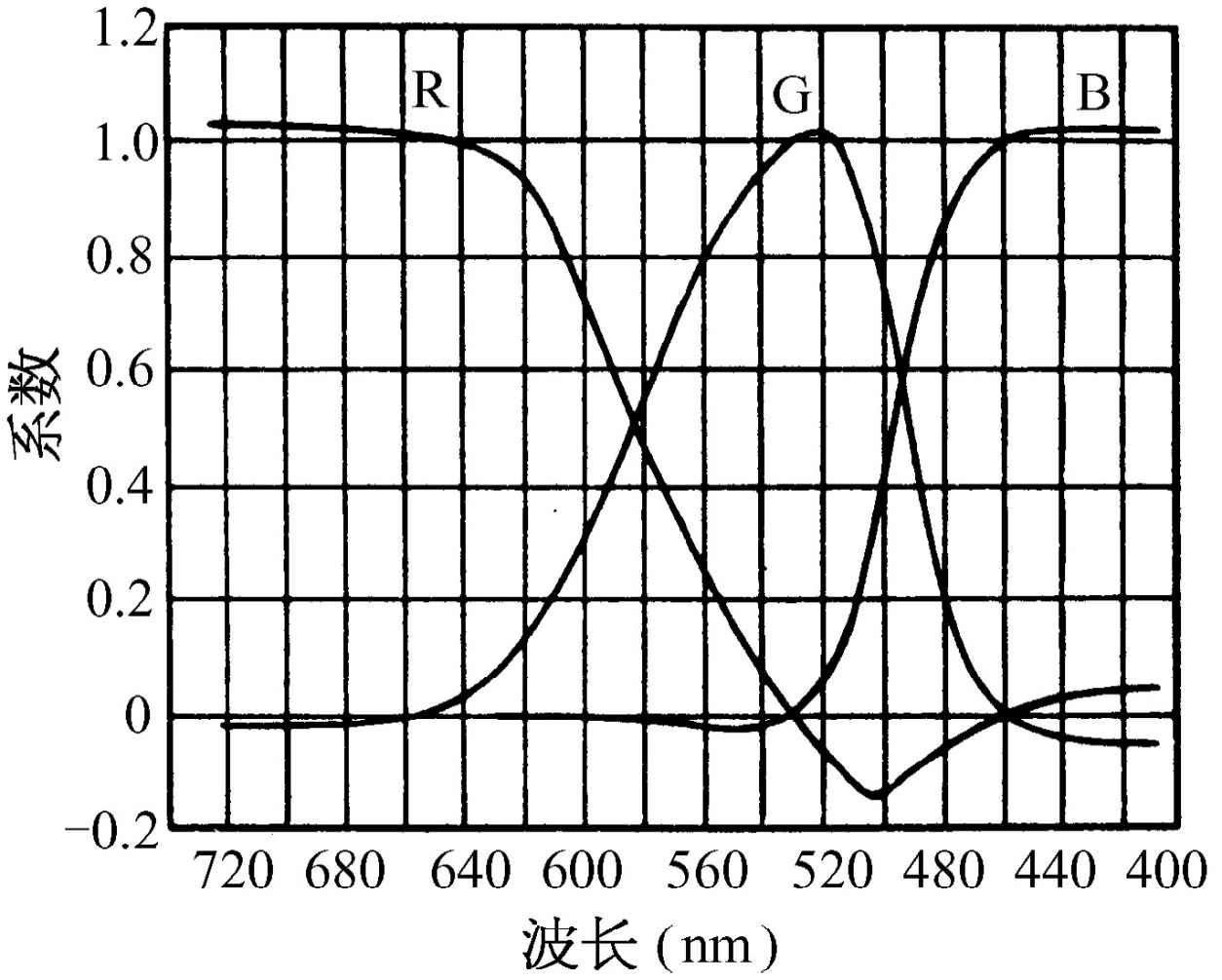
图35-5 以某组标准原色表示的纯光谱色的色系数
§35-5 色视觉的机制
谈到现在,下一步就提出这样的问题:为什么颜色的行为竟是如此?由杨和亥姆霍兹提出的最简单的理论,假设眼睛中有三种不同的感光的色素,它们有不同的吸收光谱,因此一种色素比如说在红色区吸收很强,另一种色素在蓝色区吸收很强,再一种色素在绿色区吸收很强。当我们把光照射到它们上面时,就会在三个区域内得到不同数量的吸收,而这三部分信息在大脑中、眼睛中、或某个地方以某种方式调节,以确定这是什么颜色。很容易证明,所有颜色的混合法则都符合这一假说的结果。关于这个问题曾经有过相当多的争论,因为接下来的问题当然就是要找出这种色素各自的吸收特性曲线。遗憾的是,我们发现,由于我们能以任何愿意的方式变换颜色坐标,所以用混合颜色的实验只能找到吸收曲线的各种线性组合,而不是个别色素的吸收曲线。人们曾用各种方法试图获得一条特殊的曲线,用它确实能够描述眼睛的某种特殊的物理性质。这种曲线之一是图35-3所示的亮度曲线 。在这张图上有两条曲线:一条是对于处在黑暗中的眼睛,另一条是对于处在亮光中的眼睛;后者是视锥细胞的亮度曲线。它是这样测得的,即一种色光,其最小数量应是多少才能使眼睛恰好看到它。这条曲线表明眼睛在不同光谱区内的灵敏度有多高。另外,还有一个非常有趣的方法可以测量这条曲线。假如我们取两种颜色,并使它们显示在同一区域内,再把它们一个变到另一个交换闪变,那么如果闪变频率过低,我们就能看到颜色交替地闪现。然而,随着频率的增加,这种闪变终于会在某一频率消失,这个频率依赖于光的亮度,例如说:每秒来回16次。现在,如果我们相对于这一种颜色调节另一种颜色的亮度或强度,那么到达某一强度时16 Hz频率闪变就会消失。在这样调节出来的亮度下再得到闪变,就必须回到低得多的频率,才能够看到颜色的闪变。所以我们得到频率较高时的所谓亮度闪变以及频率较低时的颜色闪变。利用这种闪变技术可以使两种颜色在“亮度相等”上相匹配。所得结果几乎与测量眼睛时使用视锥细胞观察微弱光线的灵敏度阈值所得的一样,但不是完全相同。大多数研究工作者在这方面都用闪变系统作为亮度曲线的定义。
现在,如果眼睛中有三种对颜色灵敏的色素,那么问题就是要确定每一种色素的吸收光谱的轮廓。怎样做呢?我们知道,有些人——男性人口中的百分之八,女性人口中的百分之零点五——是色盲。大多数色盲或色视觉不正常的人对颜色的变化与其他正常人相比具有不同程度的灵敏度,但他们仍需要用三种颜色来进行匹配。然而,有一些人被称为二色性色盲者 (dichromats),对于这种人任何颜色只要用两种 原色就可以匹配。于是一个明显的设想是他们缺少三种色素中的一种。如果我们能够找到三种具有不同颜色混合法则的二色性色盲者,那么一种应是缺少红色 ,另一种应是缺少绿色 ,再一种应是缺少蓝色 的色素沉积。因而通过对所有这些色盲类型的测量,我们就能确定三条曲线!结果发现果然有三种类型的二色性色盲,两种是一般的类型,第三种是极稀少的类型,从这三种类型就可以推断出色素的吸收光谱。
图35-6表示一种特殊类型的称为患绿色盲者的颜色混合。对他来说,相同颜色的轨迹不是一个一个点,而是一条一条直线,沿着每一条直线,颜色是相同的。如果像这种理论所说的,他缺少三部分信息中之一是正确的话,那么所有这些直线应该相交于一点。如果我们在这张图上仔细地进行测量,那么它们确实 完全相交。因此,很明显,这是数学家设想出来的,并不表示真实的数据!事实上,如果我们看一下具有真实数据的最新文献,就会发现,图35-6中所有直线的焦点并不准确地位于恰当的位置上。利用上图中的直线不可能找出合理的光谱;在不同区域内,我们需要用负的和正的吸收。但是如果用余斯托伐(Yustova)的新的数据,那么就会发现每一条吸收曲线到处都是正的。
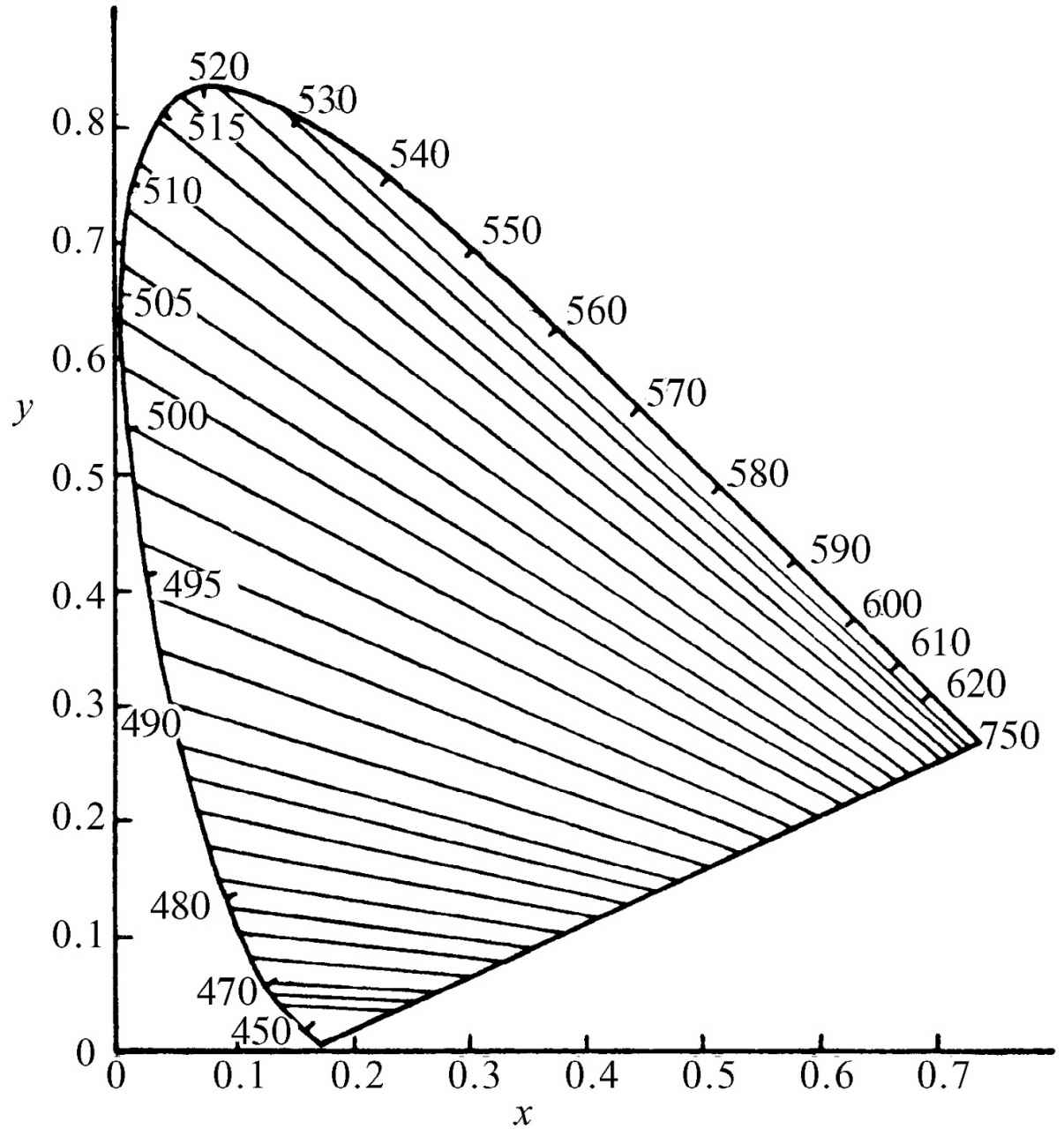
图35-6 被患绿色盲的人搞混乱的颜色轨迹
图35-7表示另一种色盲,即患红色盲的人的情况,它在靠近边界曲线的红端有一个焦点。在这种情况下,余斯托伐近似地得到了同一个位置。利用三种不同的色盲,三种色素的响应曲线最后被确定了下来,如图35-8所示。这是最终的结果吗?或许是,但对下列各点还是有一些问题,那就是三种色素的想法是否正确、色盲是否由于缺少一种色素所引起的结果,甚至关于色盲的颜色混合数据是否正确。不同的研究工作者得出不同的结果。这个领域仍在不断发展中。
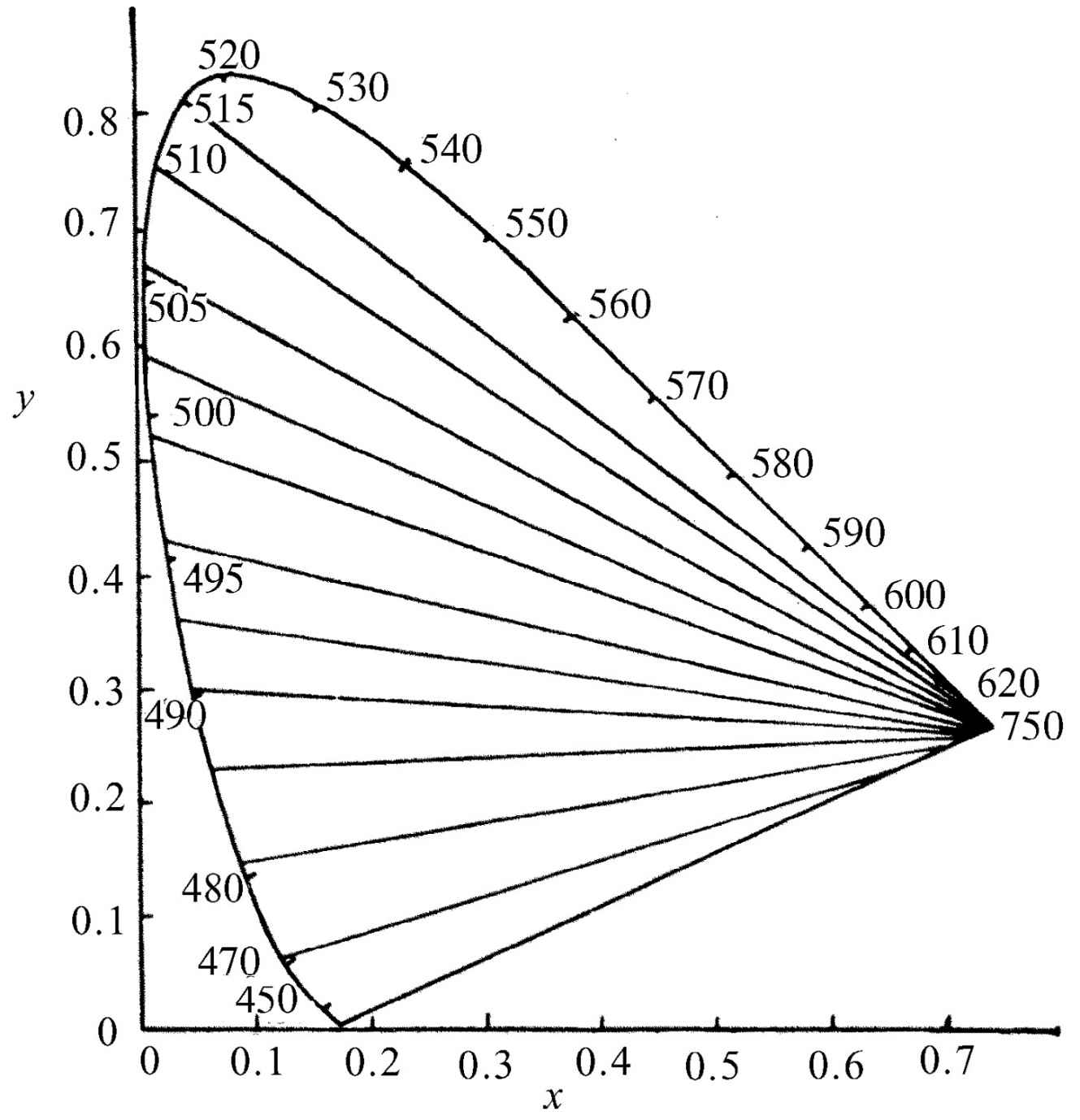
图35-7 被患红色盲的人搞混乱的颜色轨迹
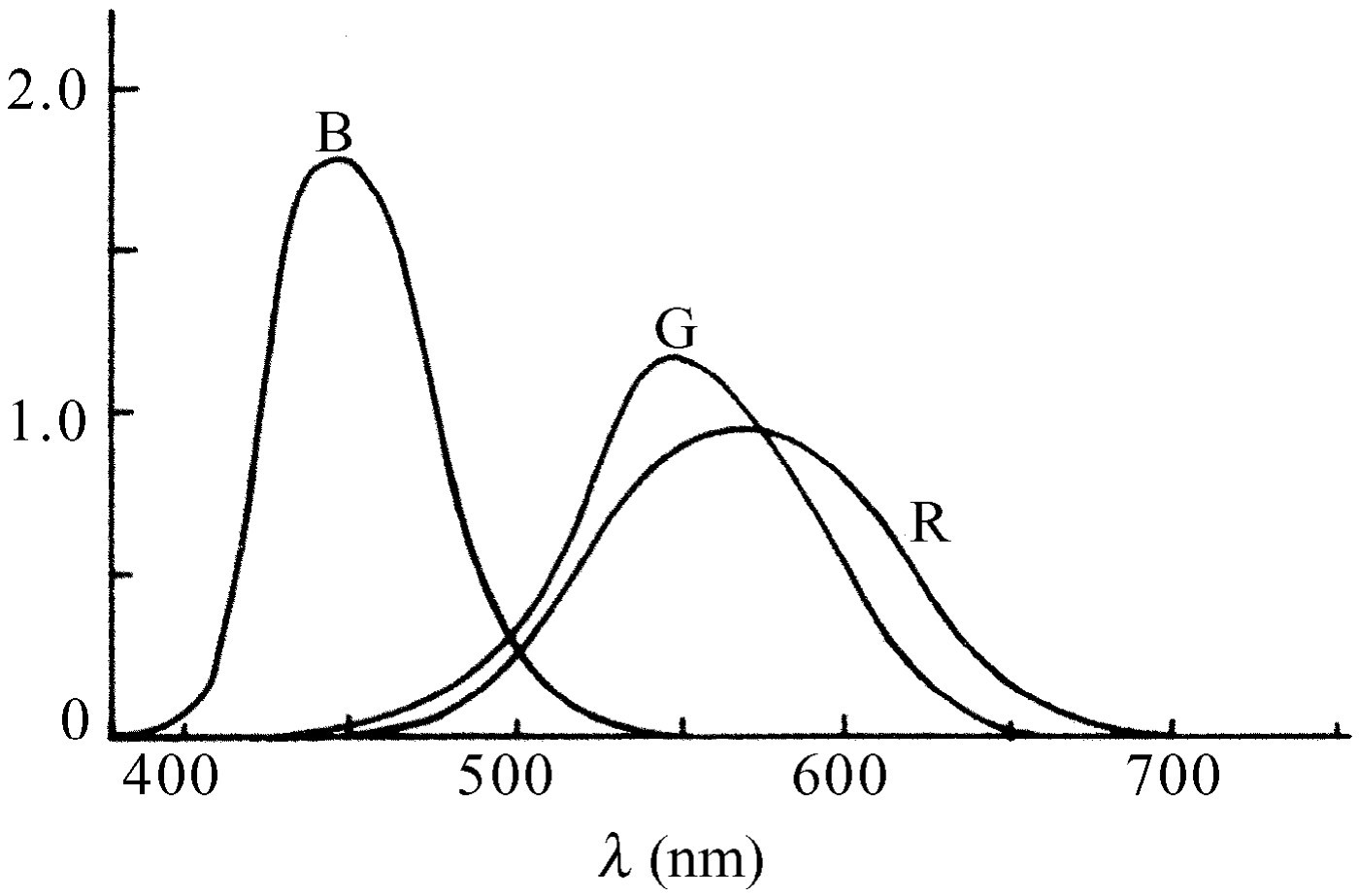
图35-8 正常三色者的接收器的光谱灵敏度曲线
§35-6 色视觉的生理化学
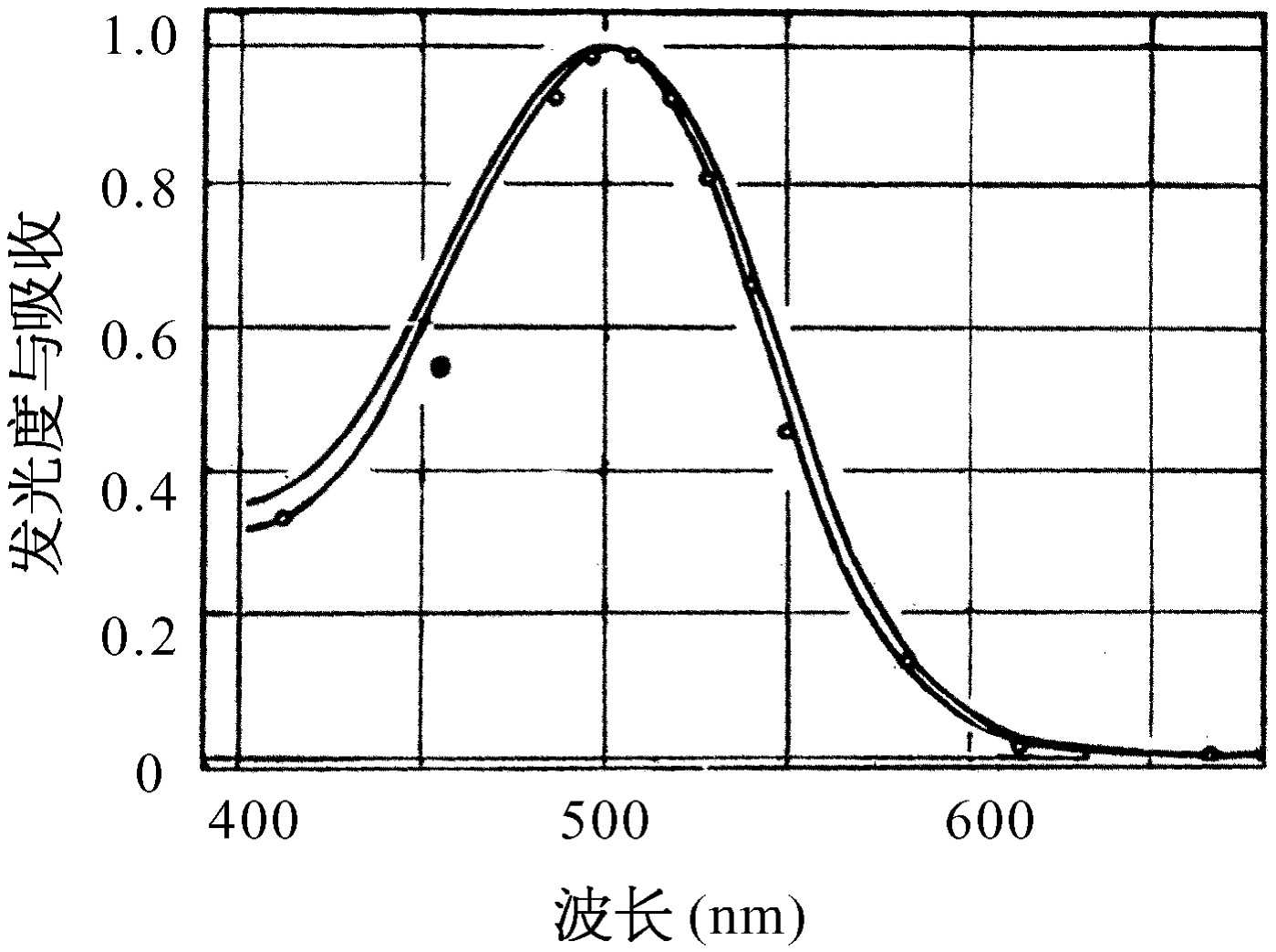
现在,怎样根据眼睛中的真实色素来核对一下这些曲线?从视网膜获得的色素主要是由一种叫做视紫质 的色素组成的。它最突出的特性是:第一,它几乎存在于每一种脊椎动物的眼睛中;第二,它的响应曲线和眼睛的灵敏度完美地相适合,像从图35-9中可以看到的那样符合得非常好。图中我们用同样的比例画出了视紫质的吸收曲线和适应黑暗的眼睛的灵敏度。这种色素显然是我们在黑暗中用来观察的色素:视紫质是视杆细胞所用的色素,它和色视觉毫无关系。这一事实是1877年发现的。即使在今天,还是可以说视锥细胞的色素从来没有在试管中获得过。1958年人们还是可以说,色素从来没有被看到过。但是从那时候起,拉什顿(Rushton)曾经用非常简单而又巧妙的技术探测到两种这样的色素。
由于眼睛对明亮的光比之对强度弱的光非常不灵敏,所以困难大概在于需要用很多视紫质来观察弱光,但不必用许多色素来观察颜色。拉什顿的想法是:让色素留在眼睛内 ,并用不论何种方法来测量它。他是这样做的。有一种仪器叫检眼镜,它把光通过眼球的晶状体送进眼睛,然后把反射回来的光聚焦在一起。使用这种仪器人们可以测量出有多少光被反射回来。这样,我们对两次 通过色素的光(被眼球的背层所反射,并且再次通过视锥细胞的色素出来的)测量了它的反射系数。自然界并不总是设计得这样美妙的。但视锥细胞有趣地被设计成这样,使得进入视锥细胞的光被来回反射,最后向下钻进顶端处的微小的灵敏点中。光一直往下进入灵敏点,在其底部被反射,而在穿过相当数量的色视觉色素后重新反射回来;而且,通过观察中央凹,那里没有视杆细胞,这样人们就不会被视紫质所搞混。但是视网膜的颜色很早以前就已被人们观察到:它是一种带橙色的粉红色。然后又看到了所有的血管和背后物质的颜色,等等。我们怎么知道看到的就是这种色素呢?回答 :首先,我们找一个患有色盲的人,他的色素较少,因此很容易对他进行分析。其次,各种色素像视紫质一样,当被光漂白后强度就有所改变。当我们把光照射它们时,它们就改变浓度。所以,在观察眼睛的吸收光谱时,拉什顿用另一束 光照射整个眼睛,使它改变色素的浓度,同时,他测量了光谱的变化 ,这个差别当然与血液的数量或者反射层的颜色等等无关,而只与色素有关。拉什顿用这种方式获得了患红色盲的人的眼睛的色素曲线,如图35-10所示。
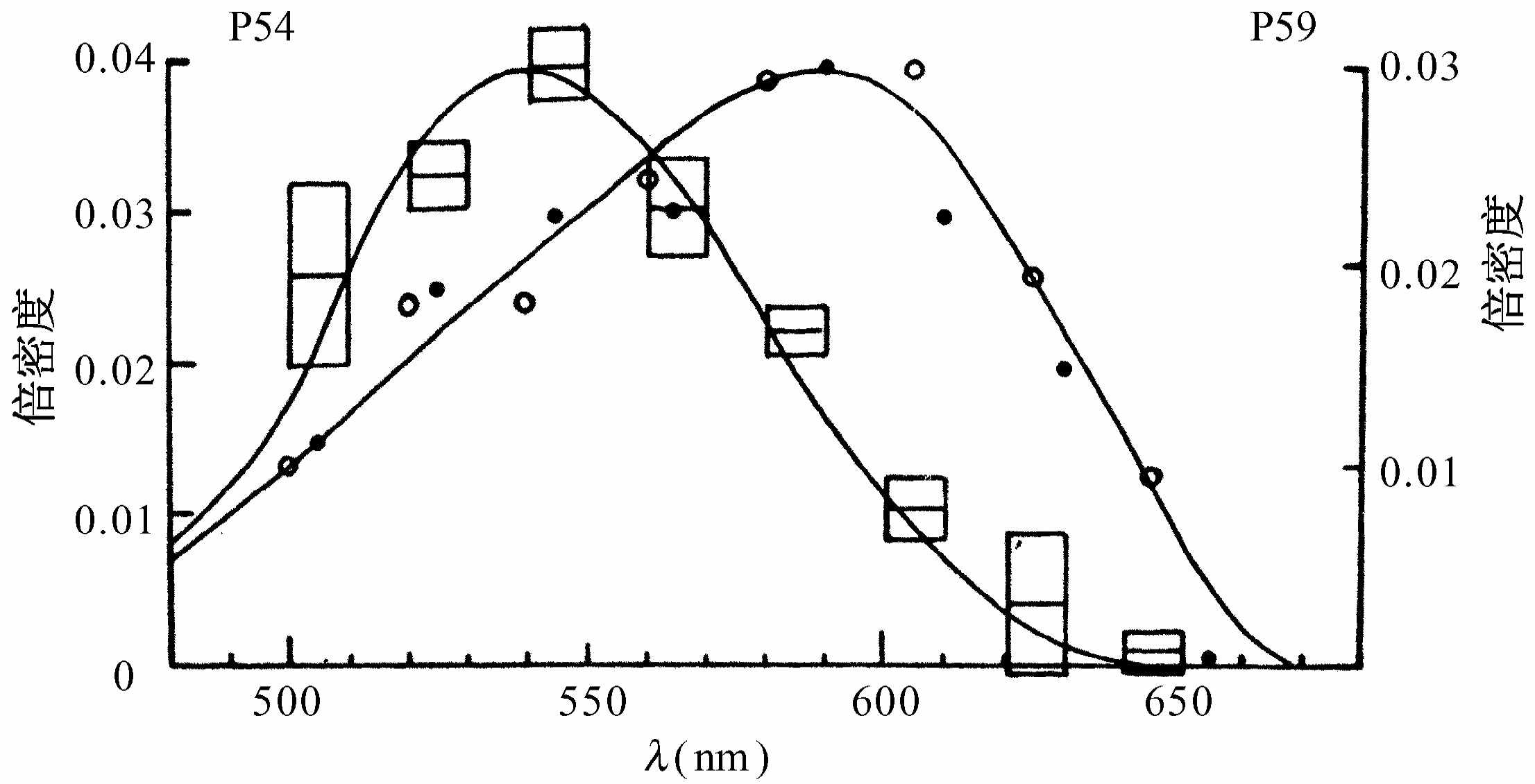
图35-10 患红色盲的人的眼睛(方块)和正常眼睛(点)的色素吸收光谱
图35-10中的第二条曲线是用正常眼睛得到的曲线。并且是在已经确定这种色素是什么色素,而把另一种用对第一种不灵敏的红色漂白之后得到的。红光对患红色盲的人的眼睛没有影响,但对正常眼睛却有影响。这样人们就能对所缺少的色素得到一条曲线。一条曲线的形状和余斯托伐的绿色曲线符合得很好,但红色曲线有少许位移。或许我们抓住了正确的线索,或许没有——最近对患绿色盲的人所进行的工作并没有显示出缺少什么确定的色素。
颜色不是光本身的物理学问题。颜色是感觉 ,不同颜色的感觉在不同情况中是不同的。举例来说,假如我们有一种由白光和红光叠加而成的粉红色光(用白色和红色所能配制的显然总是粉红色),我们就可以证明白光可以显示为蓝色。如果我们把一个物体放在光束中,它投射两个影子——一个单独为白光所照亮,而另一个为红光所照亮。对大多数人来说,物体的“白色”影子看上去是蓝色,但是如果我们不断扩大这个影子,直到它遮盖住整个屏幕,那么我们将看到它突然显示为白色,而不是蓝色!将红光、黄光和白光混合时,我们能够得到性质与此相同的其他效应。红光、黄光和白光只能产生橙黄色,等等。所以如果我们把这些光大致等量地混合在一起,我们只能得到橙色光。然而,当在这束光中投射出不同种类的影子时,那么由于颜色的各种叠加,人们得到一连串美丽的颜色,这些颜色并不存在于光本身之中(它只是橙色),而只存在于我们的感觉 之中。我们清楚地看到许多颜色完全与光束中的“物理”颜色不同。重要的是要意识到视网膜已经在“思考”光,它正在把一个区域中所能看到的东西同另一个区域中所看到的东西进行比较,虽然是不自觉的。至于它是怎样进行的,我们在这方面所知道的一切将在下一章中进行讨论。
参考文献
Committee on Colorimetry, Optical Society of America, The Science of Color , Thomas Y. Crowell Company, New York, 1953.
Hecht, S., S. Shlaer, and M.H. Pirenne, "Energy, Quanta and Vision", Journal of General Physiology , 1942, 25, 819~840.
Morgan, Clifford and Eliot Stellar, Physiological Psychology , 2nd ed., McGraw-Hill Book Company, Inc., 1950.
Nuberg, N.D. and E.N. Yustova, "Researchs on Dichromatic Vision and the Spectral Sensitivity of the Receptors of Trichromats," presented at Symposium No.8 Visual Problems of Colour , Vol.II, National Physical Laboratory, Teddington, England, September, 1957. Published by Her Majesty's Stationery Office, London, 1958.
Rushton, W.A., "The Cone Pigments of the Human Fovea in Colour Blind and Normal", presented at Symposium No.8, Visual Problems of Colour , Vol.I, National Physical Laboratory, Teddington England, September 1957. Published by Her Majesty's Stationery Office, London, 1958.
Woodworth, Robert S, Experimental Psychology , Henry Holt and Company, New York, 1938.Revised edition, 1954, by Robert S. Woodworth and H. Schlosberg.