第43章 扩散
§43-1 分子间的碰撞
迄今为止,我们只考虑了处于热平衡状态下气体中的分子的运动。我们现在要讨论当情况接近但不是精确处于平衡态时将发生什么。在远离平衡态的情况下,问题极其复杂,但在非常接近于平衡态时,我们很容易得出会出现什么。然而为了要看出会发生什么事情,我们必须回到分子动理论上去。统计力学和热力学所处理的是平衡态,但是在偏离平衡的情况下,可以说,我们只能通过一个一个原子来分析所发生的事情。
作为非平衡状态的一个简单例子,我们来考虑气体中离子的扩散。假设在气体中存在着浓度相当小的离子——即带电分子。如果在气体上施加一个电场,则每个离子将受到一个力,这个力不同于气体中的中性分子所受的力。假设没有其他分子存在,直至到达容器壁前,离子都有一个恒定加速度。但是,由于存在着其他分子,它不能这样,它的速度只在和其他分子发生碰撞并失去动量以前增加。此后再次增加速率,它又会再次失去动量。净结果是,这个离子沿着一条奇特的路径运动,但是净运动总是沿着电力的方向。我们将看到离子在作一种平均速率正比于电场的平均“漂移”,电场越强,离子跑得越快。当加上电场,并且离子沿着电场方向运动时——当然这不是 处在热平衡状态,而是力图趋向于平衡——离子位于容器的终端。利用分子动理论,我们可以计算漂移速度。
我们现在的数学水平实际上不能精确 计算将出现的事情,但是我们可以获得能显示所有基本特色的近似结果。我们可以找出事情如何随着压强、温度等变化,但是不可能精确地得出所有各项前面的正确的数值因子。所以,在推导过程中,我们将不去为数值因子的精确值而担心。这只有使用非常细致的数学处理方法才能得出。
当我们考虑在非平衡状态下将会出现什么之前,需要稍微仔细地考察热平衡状态下的气体还会发生什么情况。比如说,我们要知道分子相继两次碰撞之间的平均时间。
显然,任何分子会以一种无规则的方式与其他分子作一连串碰撞。在一段相当长的时间T 中,一个特定的分子具有一定的碰撞次数N 。如果使时间加倍,碰撞次数也将加大一倍。可见碰撞次数正比于时间T 。我们可以将这一点写成
N =T /τ .(43.1)
这里将比例常数写为1/τ ,常数τ 具有时间的量纲,并且是碰撞之间的平均时间。例如,假定在1 h内有60次碰撞,τ 就是1 min。我们将说,这个τ (1 min)就是碰撞之间的平均时间 。
我们常常会提出这样的问题:“在下一个很短的时间间隔 dt 内,一个分子受到一次碰撞的机会 是多少?”可以直接想到,答案是dt /τ 。但是我们要作出一个更使人信服的论证。假设分子数N 很大。在下一个时间间隔dt 内将发生多少次碰撞?如果处在平衡态,任何东西对时间的平均 值不变。所以N 个分子在时间dt 内发生的碰撞次数与一个 分子在时间N dt 内发生的碰撞次数相同。我们知道这个数目是N dt /τ 。所以N 个分子在时间dt 内的碰撞次数是N dt /τ ,而任何一个分子作一次碰撞的机会或者概率都正好是1/N ,或者正像我们上面所猜测的那样,是(1/N )(N dt /τ )=dt /τ ,这就是说,在时间dt 内受到一次碰撞的分子数占总分子数的比例为dt /τ 。举一个例子来说,如果τ 是1 min,那么在1 s内受到碰撞的分子所占的比例是1/60。当然,这意味着,占总数1/60的分子正好和那些下一个时刻就会碰撞的分子靠得足够近,因而它们的 碰撞将在下一个1 min内发生。
当我们说碰撞之间的平均时间τ 是1 min时,并不意味着所有的碰撞都分别在正好相隔1 min时发生。某一特定的分子并不要等1 min后才有另一次碰撞。相继两次碰撞间的时间完全是可变的。我们后面的工作也并不需要知道它。但是我们可以将“两次碰撞之间的时间是什么?”这样的问题略加改动。我们知道,对于上述情况,平均 时间是1 min,但是我们或许还想知道,比方说,在2 min内不发生碰撞的机会有多大?
我们将找出对以下的一般性问题的答案:“一个分子在时间t 内一次碰撞也不发生的概率是多少?”在某一个任意时刻——可以称为t =0——我们开始注视一个特定的分子。直到时刻t 它还未和另一个分子碰撞的机会有多大?为了计算这个概率,我们观察在容器内所有N 0 个分子将发生什么情况。在等了一段时间t 后,它们中的某些已受到碰撞。令N (t )为直到时间t 为止没有 受到碰撞的分子数。当然,N (t )小于N 0 。我们可以求得N(t)因为我们知道它随时间怎样变化。如果我们知道了直到t为止的未碰撞分子数是N(t),那么,直到t +dt 为止的未碰撞分子数N (t +dt )小于 N (t ),其差值就是在dt 内发生碰撞的分子数。我们上面已用平均时间τ 将dt 时间内所发生的碰撞数写为
dN =N (t )dt /τ .
于是有方程式
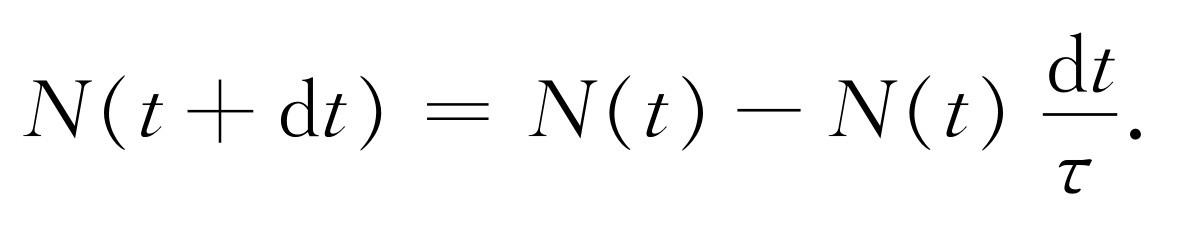 (43.2)
(43.2)
按照微分的定义,左边的量N (t +dt )可写为N (t )+(dN /dt )dt ,将此代入后,方程式(43.2)就成为
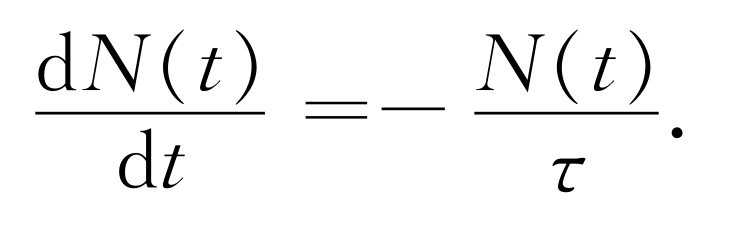 (43.3)
(43.3)
在dt 间隔内损失的分子数正比于现在的分子数,反比于平均寿命τ 。如果把式(43.3)改写为
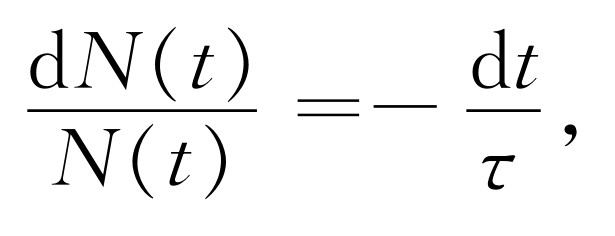 (43.4)
(43.4)
就很容易积分。每一边都是个全微分,所以积分是
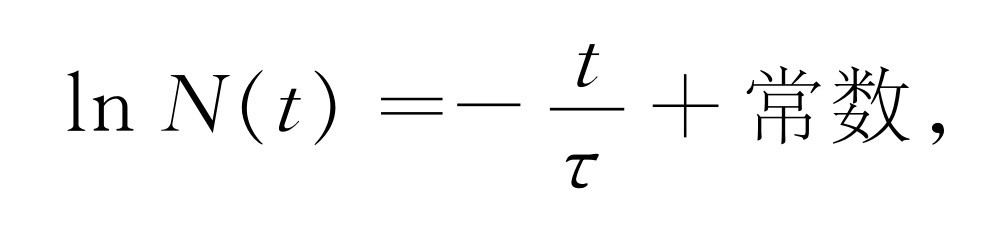 (43.5)
(43.5)
也就是说
N (t )=常数·e-t / τ .(43.6)
我们知道常数必定正好是现在的总分子数N 0 ,因为从t =0开始它们全都等待着它们的“下一次”碰撞。我们可以把结果写为
N (t )=N 0 ·e-t / τ .(43.7)
如果我们要知道不发生碰撞的概率 P (t ),可以将N (t )除以N 0 来得到,于是
P (t )=e-t / τ .(43.8)
我们的结果是:某个分子直到时间t 还没有发生碰撞的概率是e-t / τ ,这里的τ 是两次碰撞间的平均时间。概率从t =0时的1(或者必然发生)开始随t 越来越大而变小。一个分子在等于τ 的时间内还不发生一次碰撞的概率是e-1 =0.37…。两次碰撞之间的时间大于平均碰撞时间的机会小于1/2。这是完全正确的,因为有足够多的分子在远大 于平均碰撞时间的时间前不发生碰撞,因而平均碰撞时间仍然可以是τ 。
我们原来定义τ 为碰撞之间的平均时间。由式(43.7)得到的结果也表明从任 一时刻开始到下 一次碰撞的平均时间也是τ 。我们可以证明这个多少有点使人惊讶的事实:在任意选定的初始时刻后的时刻t ,在时间间隔dt 内,受到下一次 碰撞的分子数是N (t )dt /τ 。当然,这些分子的“在下一次碰撞前的时间”正好是t 。“在下一次碰撞前的平均时间”可以用通常求平均值的方法写为

利用式(43.7)得出N (t ),并计算积分,我们确实发现τ 是从任一 时刻到下一次碰撞的平均时间。
§43-2 平均自由程
描写分子碰撞的另一种方式是不谈碰撞之间的时间 ,而谈碰撞之间分子走了多远 。如果我们说碰撞之间的平均时间是τ ,而分子的平均速度是v ,我们就可预期碰撞之间的平均距离 (记为l )正好是τ 与v 的乘积。两次碰撞之间的距离通常称为平均自由程
平均自由程l =τv .(43.9)
在本章中,我们对每一个特殊场合下所指的究竟是哪一类平均 并不那么在意。各种可能的平均——权重平均,方均根,等等——全都近似相等,只差一个接近于1的因子。不管怎样,为了得到正确的数值因子,必须进行详细的分析,因此我们不必担心在每一种特殊情况下需要用哪种平均值。我们也要提醒读者注意,这里对某些物理量采用的代数符号(如平均自由程的l )并非根据共同接受的习惯方式,主要是因为没有被普遍采纳的记法。
正如一个分子在短时间dt 内进行一次碰撞的机会是dt /τ 一样,它在距离dx 内进行一次碰撞的机会是dx /l 。按照上面采用过的同样论证,读者可以证明一个分子在下一次碰撞前至少跑过距离x 的概率是e-x / l 。
一个分子在与其他分子碰撞前走过的平均距离——平均自由程l ——取决于它周围有多少分子以及这些分子的“大小”,即取决于它面临的“靶”有多大。我们通常用“碰撞截面”来描写在一次碰撞中靶的有效“大小”,这与核物理或光散射问题中采用的概念相同。
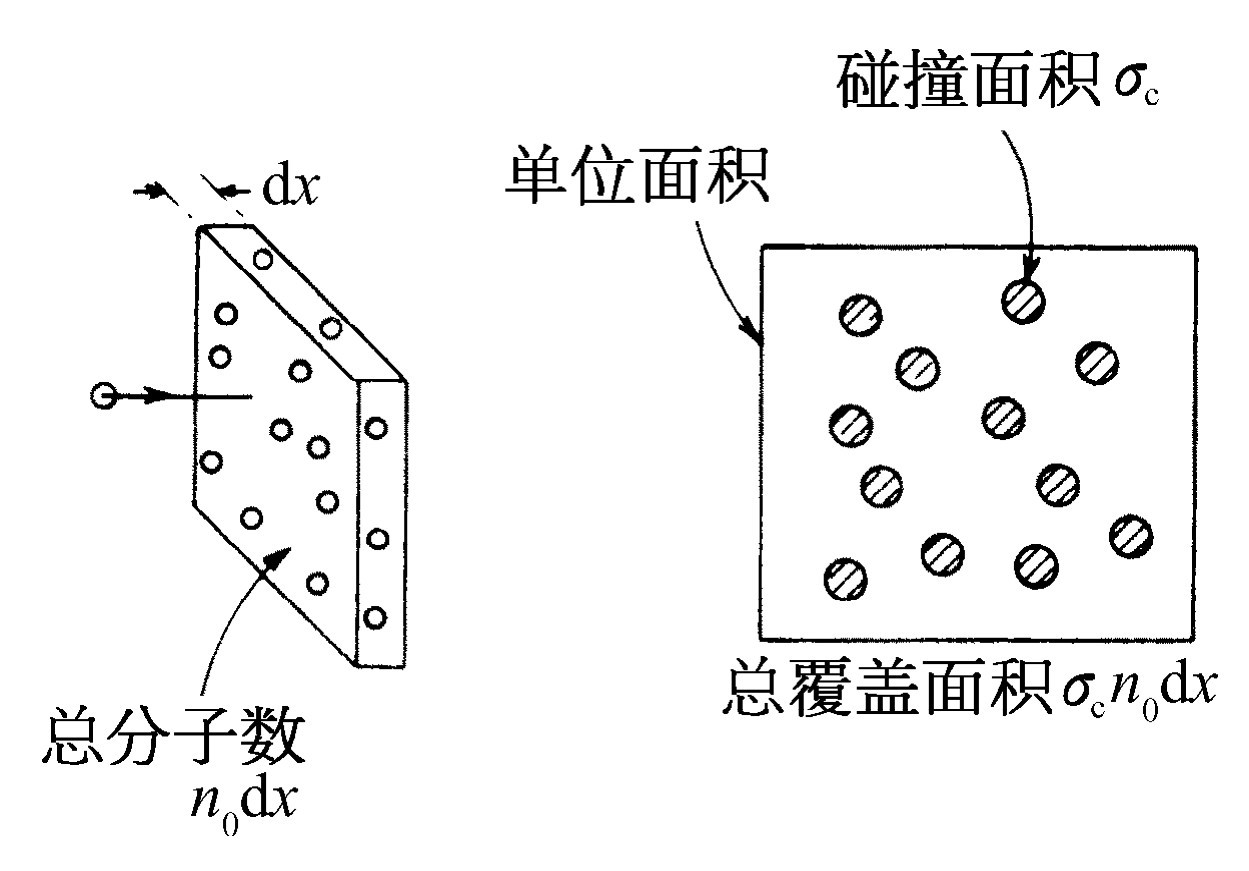
考虑一个运动粒子在气体中移动距离dx 的情况。气体中每单位体积内有n 0 个散射体(分子)(图43-1)。观察与所选定的粒子运动方向相垂直的每单位面积,将发现那里有n 0 dx 个分子。如果每个分子提供一个有效碰撞面积,即通常说的“碰撞截面”σ c ,则散射体所覆盖的总面积为σ c n 0 dx 。
所谓“碰撞截面”指的是这样一种面积,只要所研究的分子和一个特定的分子相碰撞,这种分子的中心必定处在那块面积内。假如分子是一些小球(一幅经典图像),我们就可以预期σ c =π (r 1 +r 2 )2 ,这里的r 1 和r 2 是两个碰撞体的半径。分子发生一次碰撞的机会是散射分子所覆盖的面积与总面积之比,总面积可取为一个单位。故在距离dx 内发生一次碰撞的概率正好是σ c n 0 dx
在dx 中发生一次碰撞的机会=σ c n 0 dx .(43.10)
我们从上面已经看到过在dx 内发生一次碰撞的机会也可用平均自由程l 写为dx /l ,与式(43.10)比较,就可以把平均自由程与碰撞截面联系起来
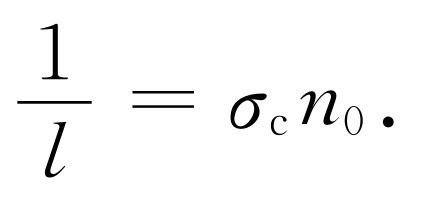 (43.11)
(43.11)
如果把它写为
σ c n 0 l =1,(43.12)
将更便于记忆。
这个公式可以这样来看,当分子经过距离l ,在这段距离内散射分子正好能够 覆盖住整个面积时,平均说来将会发生一次碰撞。在一个长度为l 、底面积为单位面积的圆柱形体积内,有n 0 l 个散射体,如果每一个散射体具有面积σ c ,则总的覆盖面积是n 0 lσ c ,它正好是一个面积单位。当然,整块面积并没有被覆盖住,因为有些分子被其他分子遮盖了一部分。这就是为什么有些分子在碰撞前跑得比l 远的原因。分子在跑过距离l 的这段时间内进行了一次碰撞,这只是就平均 而言。从平均自由程的测量中,我们可以确定散射截面σ c ,并与建立在更详尽的原子结构理论基础上算出的结果进行比较。但这是一个不同的课题!所以我们还是回到非平衡态的问题上来。
§43-3 漂移速率
我们来描述一个或几个分子发生的行为,它们在有的方面与气体中的大多数分子不同。我们把“大多数”分子称为“背景”分子,而跟背景分子不同的分子则称为“特殊”分子,或简称为S分子。任何原因都可以使分子变成特殊:比如它可能比背景分子重一些,可能有不同的化学成分,还可能带有电荷——也就是说是一个在中性分子(不带电荷分子)背景下的离子。由于S分子在质量或电荷上的不同,S分子可能受到的力与作用在背景分子上的力不同。考虑了在这些S分子上所发生的情况后,我们就能够理解一些基本效应,它们在许多不同的现象中以相似的方式出现。可以列举几个例子:气体的扩散、电池中的电流、沉淀、离心分离,等等。
我们先集中注意以下基本过程:在背景气体中的一个S分子受到某种特殊的力 F 的作用(比如说可能是重力或电力),此外 它还受到由于和背景分子碰撞而产生的比较寻常的力。我们现在来描写S分子的一般行为。就细节 来说,它所表现出的就是一再与其他分子碰撞,一会儿冲到这里,一会儿冲到那里。但是,如果我们留心观察的话,会注意到在力 F 的方向上,这个分子确实有某些净移动。可以说,在它的无规则运动上再叠加了一个漂移 运动。我们希望知道这个分子由于力 F 而产生的漂移速度 有多大。
如果我们从某个时刻开始观察S分子,可以预期它处在两次碰撞之间的某个位置上。除了它在最后一次碰撞中所留下的速度外,还获得了由于力 F 产生的某一速度分量。在一个短时间内(平均而言,在τ 时间内),它受到一次碰撞,因而开始沿着一个新的轨道运动。它将具有一个新的初速度,以及由 F 产生的加速度。
为了简单起见,暂时假设每次碰撞后,S分子都获得一个“全新”的开始。也就是说,它根本不记得由 F 产生的过去的加速度。如果我们的S分子比背景分子轻得多,这是一个合理的假说,但一般说来它肯定不成立。以后我们将讨论一种改进的假设。
所以,暂时我们假定S分子在每次碰撞后所具有的速度沿任何方向的可能性都是相等的。这个初始速度是各向同性的,而且对任何净运动均无贡献,所以在一次碰撞后,我们将不必考虑它原来的速度。每个S分子除了它的无规则运动外,在任何时刻,还具有自上一次碰撞起由力 F 的作用而引起的沿 F 方向的附加速度。速度的这一部分的平均 值是多大呢?它正是加速度 F /m (这里的m 是S分子的质量)乘以自上一次碰撞以来的平均 时间。而自上一次 碰撞以来的平均时间必定和直到下一次 碰撞为止的平均时间相同,前面我们曾把它称为τ 。当然,由 F 所引起的平均 速度正是我们所说的漂移速度,这样得到关系式
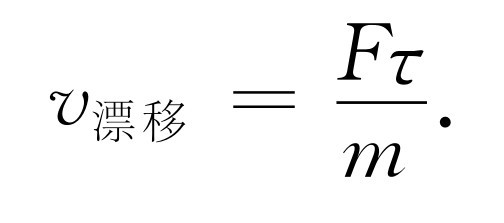 (43.13)
(43.13)
这个基本关系式是本章课题的核心。在确定τ 是什么时,会出现某些复杂性,但是基本过程由式(43.13)确定。
你们会注意到,漂移速度正比 于力。遗憾的是,对比例常数没有通用的名称。对于每类不同的力采用了不同的名称。在电学问题中,力可以写成电荷乘以电场 F =q E ,而速度和电场 E 之间的比例常数通常称为“迁移率”。尽管有可能出现一些混淆,对于任何 力,我们都将采用迁移率 这个词来表示漂移速度与力的比值,即写为
v 漂移 = μ F ,(43.14)
而一般地称 μ 为迁移率。由式(43.13)有
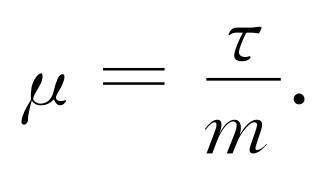 (43.15)
(43.15)
迁移率正比于碰撞之间的平均时间(τ 长时使S分子运动减慢的碰撞也少),并反比于质量(较大的惯性意味着在碰撞之间获得的速率较小)。
要想得到式(43.13)(它是正确的)中的正确数值系数,必须小心一些。为了避免混淆起见,我们还应当指出,在论证中包含着一个只有经过小心而详尽的考察才能领会的微妙之处。不管表面上如何,为了说明确实存在困难,我们以一种似乎合理但却是错误 的方式重复一次能导出式(43.13)的论证(这种方式可以在许多教科书上找到)。
我们本来可以这样说:碰撞之间平均时间是τ 。在一次碰撞后粒子以无规速度开始运动,但在两次碰撞之间它得到了某个附加速度,并且等于加速度乘以时间。由于到下一次 碰撞所需的时间为τ ,那时它具有(F /m )τ 的速度。在碰撞开始时,它的速度为零。所以在两次碰撞之间,平均说来,速度是末速度的一半,因而平均漂移速度为Fτ /2m 。但这个结果是错误的!而式(43.13)才是正确的,虽然这些论证听起来同样使人满意。第二个结果之所以不正确,其理由较为微妙。它与下述情况有关:有论证中,似乎所有的碰撞间隔时间都是平均时间τ 。事实上,某些时间比平均值短,另一些时间又比平均值长。短的时间出现得较频繁 ,但是对漂移速度的贡献却较小 ,因为它们提供给粒子进行“真正得以运动”的机会较小。如果计及碰撞间自由时间的分布,可以证明没有从第二种论证中得到的因子1/2。发生错误的原因在于企图通过简单的论证将平均末速度 与平均速度本身联系起来。这种联系不是简单的,所以最好还是集中注意我们所想要的东西本身,即平均速度。我们给出的第一个论证直接地——并且正确地——确定了平均速度!但是也许我们现在可以看出,为什么在初步的推导中,一般地说我们并不企图得出所有正确的数值系数!
现在回来讨论我们的简化假设,即每次碰撞把所有与过去运动有关的记忆全部消除掉——每次碰撞后都有一个全新的开始。假如S分子是在较轻的背景分子中的一个较重的物体,那么在每次碰撞中S分子将不会丢失它“前进”的动量。在它的运动再次“无规则化”以前,还要经过几次碰撞。因此我们应该假设,在每次碰撞中——平均说来在每一个时间τ 内——S分子将失去其一定比例的动量。我们不打算讨论细节,而只是说明结果等价于用一个新的较长的τ ——它相应于平均“忘却时间”,即“忘却”它的前进动量的平均时间——来代替平均碰撞时间τ 。对τ 作了这样一个解释,我们就可以把式(43.15)运用到那种不完全像起先所假设的那样简单的情况中去。
§43-4 离子电导率
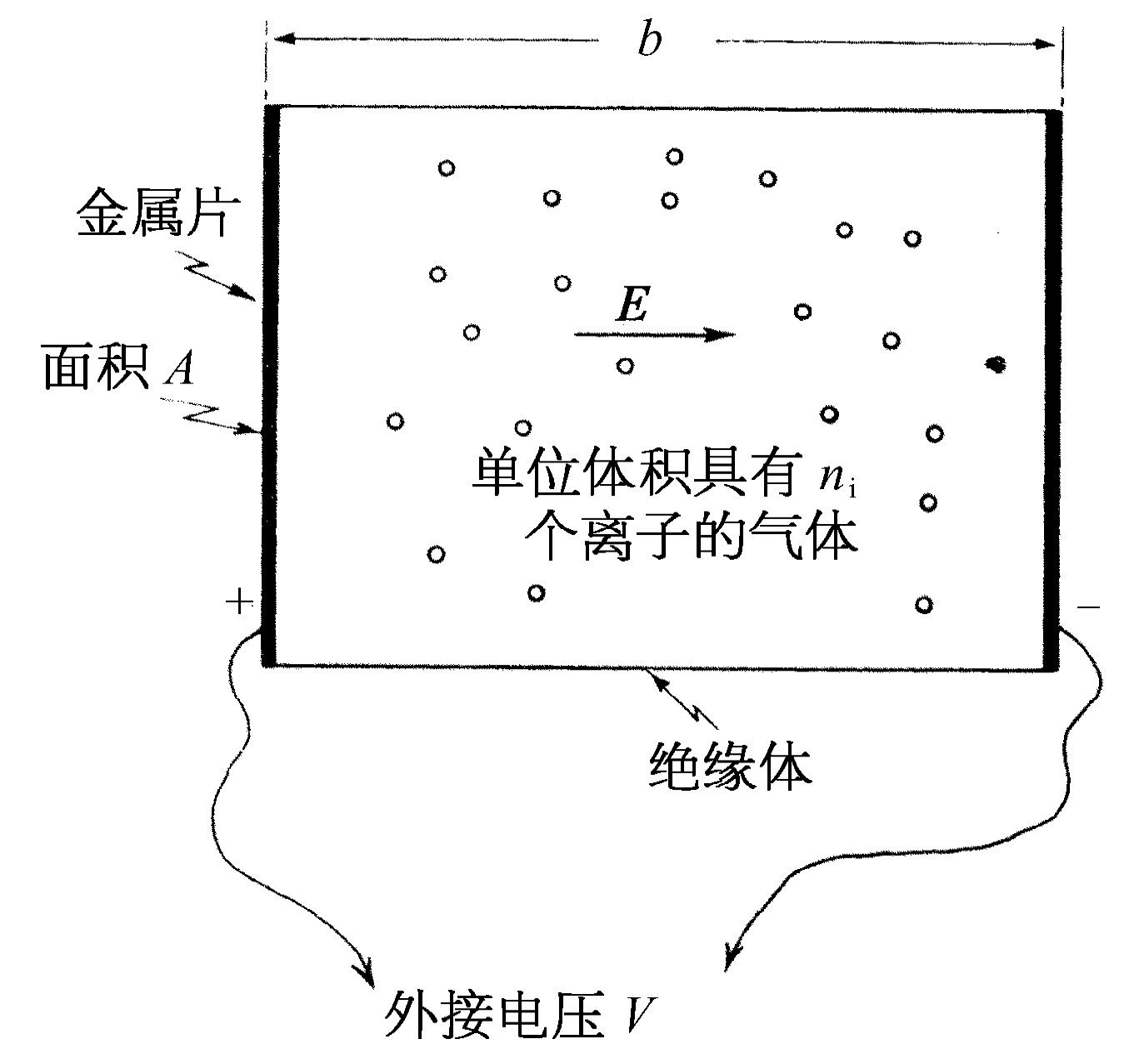
现在我们把所得结果运用到一个特殊情况中去。假设在一个容器内盛有气体,其中也有某些离子——带净电荷的原子或分子。图43-2描绘了这一情况。如果容器的两个正对面的器壁都是金属板,我们可以将它们联在电池的正负极上,从而在气体内产生一个电场。电场使离子受到作用力,这样它们开始向这一块或那一块极板漂移,引起一个电流,而带有离子的气体的行为就像一个电阻器。由漂移速度算出离子流后,就可以算出电阻。我们特别要问:电流与加在两板之间的电位差V 的关系如何?
假设我们的容器是一个长方形的盒子,长为b ,横截面积为A (图43-2)。如果从一块极板到另一块极板的电位差或电压降是V ,极板之间的电场E 就是V /b (电势就是使单位电荷从一块极板跑到另一块极板所做的功。在单位电荷上的力是 E 。如果两极板之间的任何地方 E 都相同——在我们这里这是一个足够好的近似,那么电场在单位电荷上所做的功正好是Eb ,所以V =Eb )。作用在气体的一个离子上的特殊的力是q E ,这里q 是离子的电荷。因而离子的漂移速度是 μ 与这个力的乘积,即
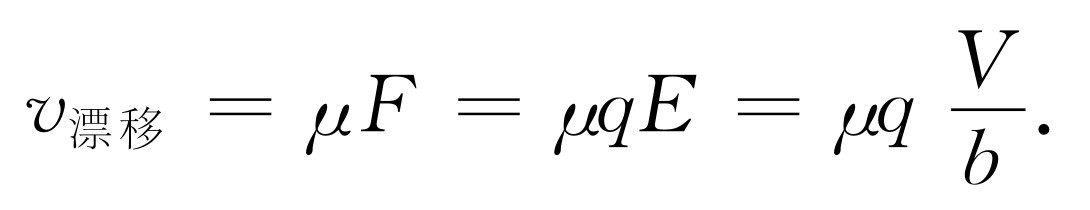 (43.16)
(43.16)
电流I 是单位时间内流过的电荷。抵达两块极板之一的电流由单位时间内到达这块极板的离子的总电荷给出。如果离子向这块极板漂移的速度是v 漂移 ,则在距离(v 漂移 T )内的离子将在时间T 内到达这块极板。如果每单位体积内有n i 个离子,则在T 时间内到达极板的离子数为(n i Av 漂移 T )。每个离子带电荷q ,故有
在时间T 内收集的电荷=qn i Av 漂移 T .(43.17)
电流I 是在T 时间内所收集的电荷再除以T ,这样
I =qn i A v 漂移 ,(43.18)
用式(43.16)的v 漂移 代入,就有
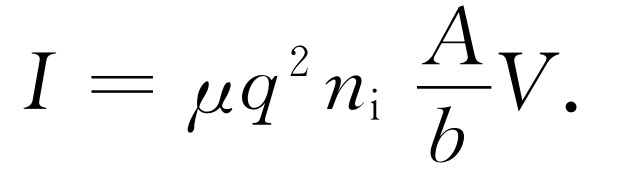 (43.19)
(43.19)
我们发现电流正比于电压,这正好是欧姆定律的表达形式,而电阻R 是比例常数的倒数
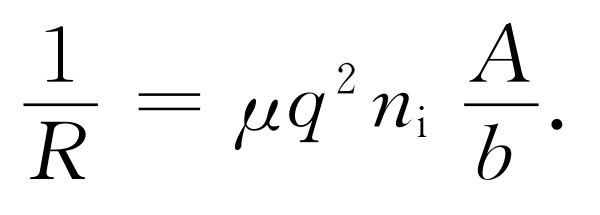 (43.20)
(43.20)
这样我们就得到了电阻与分子的性质n i 、q 和 μ 之间的一个关系式, μ 又取决于m 和τ 。如果由原子的测量中知道n i 与q ,就可用R 的测量来确定 μ ,由 μ 还可以确定τ 。
§43-5 分子扩散
现在我们转到另一类问题和另一类分析——扩散理论。假设有一个处在热平衡状态的气体容器,我们在容器中的某处放入少量不同种类的气体。我们把原来的气体称为“背景”气体,新的气体称为“特殊”气体。特殊气体将开始扩展到整个容器中,但是由于有背景气体的存在,它只能缓慢地扩展开来。这种缓慢的扩展过程称为扩散 。扩散过程主要由特殊气体的分子与背景气体的分子之间的碰撞所控制。经过大量碰撞后,结果特殊分子或多或少均匀地遍布整个容器。我们必须十分小心,不要 把气体的扩散和可能由于对流引起的大量分子的总体输运现象混为一谈。更一般地说,两种气体的混合通常都是由对流和扩散组合而成的。我们现在感兴趣的只是那种不存在“风生流”的情况。气体只是由于分子运动和扩散而扩展的。我们希望算出扩散有多快。
现在我们来计算由于分子运动而引起的“特殊”气体分子的净的流动 。只有在分子的分布上存在某种不均匀性时,才会有净的流动,否则,所有分子运动取平均后不会有净的流动。我们首先考虑沿x 方向的流动。为此设想一个表面垂直于x 轴的平面,并计算经过这个平面的特殊分子数目。为了得到净分子流,我们必须把沿正x 方向通过平面的分子数计为正的,然后减去 沿负x 方向通过平面的分子数。我们曾多次看到,在时间ΔT 中经过一个表面积的分子数等于在该表面和与之相距v ΔT 处的表面间的体积内的分子数(注意这里的v 是分子的实际速度,而不是漂移速度)。
为了简化代数运算,取平面面积为一个单位面积。因而从左向右(以向右表示正x 方向)通过的特殊分子数是n - v ΔT ,这里n - 是左边每单位体积的特殊分子数(实际上差一个2左右的因子,但我们不去管这些因子)。类似地,从右向左通过平面的分子数是n + v ΔT ,这里n + 是平面右边的特殊分子数密度。如果我们称分子流为J ,即单位时间通过单位面积的净分子流,则有
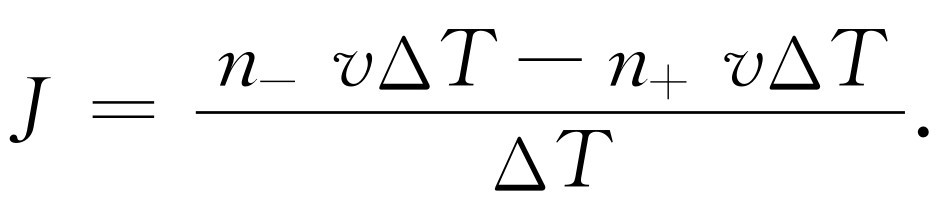 (43.21)
(43.21)
或
J =(n - -n + )v .(43.22)
对n - 和n + 将用什么值呢?当我们说“左边的密度”时,究竟指的是离左边多远 距离处的密度?我们应当选择分子开始“飞行”的那个地方的密度,因为开始 这种旅行的分子数由在那个地方的分子数来决定。因此n - 应当是在左边的距离等于平均自由程l 处的密度,而n + 则是在我们的假想平面右边l 处的密度。
如果考虑用一个称为n a 的x 、y 与z 的连续函数来描写特殊分子在空间的分布,这将是方便的。n a (x ,y ,z )指的是中心在(x ,y ,z )的小体积元中的特殊分子数密度。利用n a ,可以将差(n + -n - )表示为
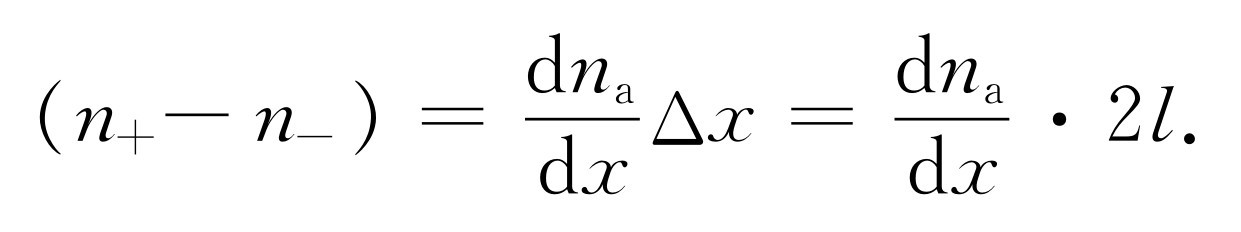 (43.23)
(43.23)
将这个结果代入式(43.22)并略去因子2,得
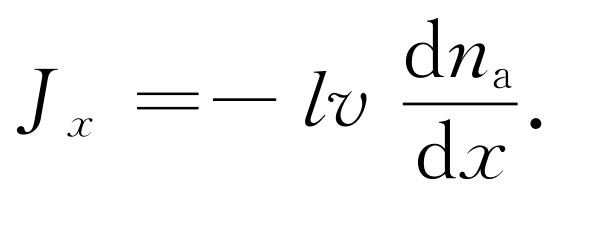 (43.24)
(43.24)
我们发现,特殊分子流正比于密度的微商,或者说正比于有时称为密度“梯度”的那个量。
显然,我们已经作了某些粗略的近似。除去略掉几个2之类的因子外,我们在原来应当用v x 的地方用了v ,并且还假设了n + 与n - 是离开假想平面垂直距离为l 的两个地方的值,而对于那些没有垂直地飞过平面元的分子来说,l 应该是离开平面的斜向距离。所有这些都可以改进,更仔细的分析结果表明,式(43.24)的右边应乘以1/3,所以更好的答案是
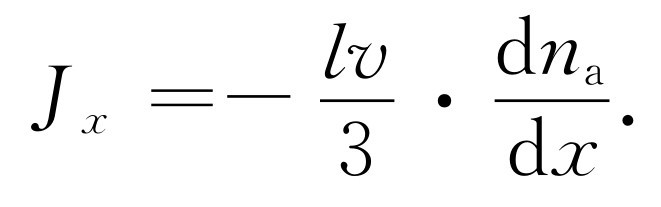 (43.25)
(43.25)
对y 方向与z 方向可以写出类似的方程式。
扩散流J x 与密度梯度dn a /dx 可以由宏观的观察来进行测量。它们从实验上测得的比值称为“扩散系数”D ,这样
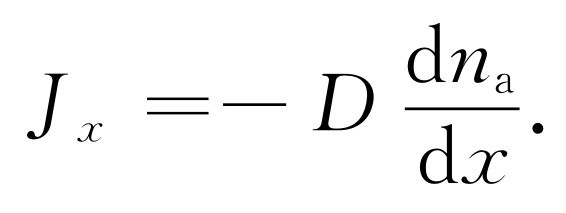 (43.26)
(43.26)
我们已经能够表明,对于气体来说
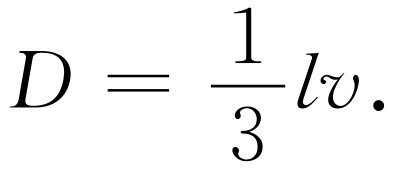 (43.27)
(43.27)
到目前为止,在本章中已考虑了两种不同的过程:迁移率 ,即由于“外”力而引起的分子的漂移;扩散 ,即仅由内力和无规则碰撞引起的分子的扩展。然而,在它们之间存在一个关系,因为它们两者从根本上说都依赖于分子的热运动,而在两种计算中都出现平均自由程l 。
如果在式(43.25)中,以l =vτ 及τ = μ m 代入,我们就有
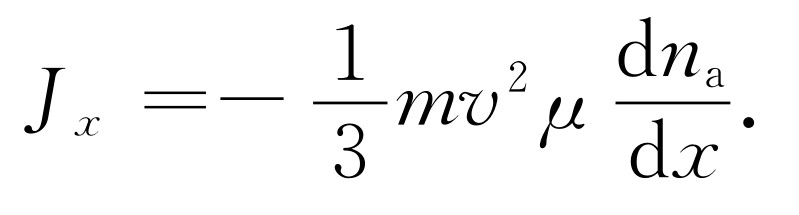 (43.28)
(43.28)
但mv 2 只取决于温度。回想一下
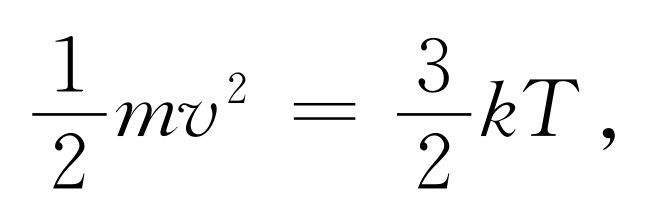 (43.29)
(43.29)
则
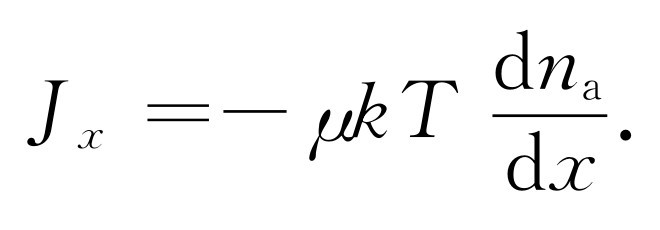 (43.30)
(43.30)
我们发现扩散 系数D 正是kT 乘以迁移率 μ
D = μ kT .(43.31)
实际情况是式(43.31)的数值系数是完全正确的——不用再加上什么别的因子来修正我们的粗糙假设。事实上,可以证明,即使在我们简单计算的细节完全不适用的复杂情况中(例如,液体中微粒悬浮的情况),式(43.31)也必定同样正确。
为了说明式(43.31)一般来说也必然正确,我们将以另一种方式,即只使用统计力学的基本原则来推导它。设想一种存在“特殊”分子的梯度的情况,按照式(43.26),将有一个正比于密度梯度的扩散流。现在我们在x 方向上施加一个力场,使每个特殊分子感受到力F 。按迁移率 μ 的定义 ,将出现一个由下式决定的漂移速度,即
v 漂移 = μ F .(43.32)
利用我们通常的论证,漂移流 (单位时间内通过单位面积的净分子数)将是
J 漂移 =n a v 漂移 ,(43.33)
或
J 漂移 =n a μ F .(43.34)
现在,我们来调整 力F 使得由它引起的漂移流刚好与扩散流平衡 。这样,在我们的这些特殊分子中不存在净流 。于是有
J x +J 漂移 =0,
或
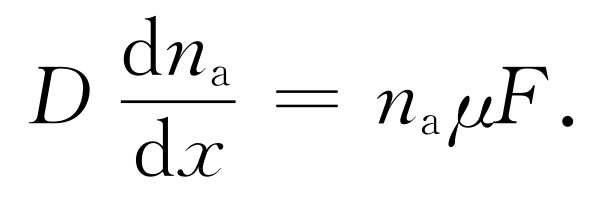 (43.35)
(43.35)
在“平衡”条件下,我们找到了一个稳定的(对时间说来)密度梯度
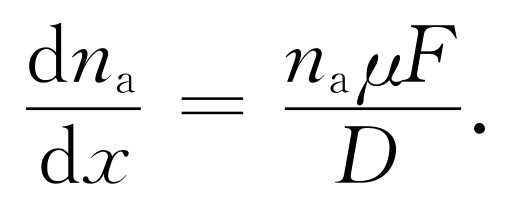 (43.36)
(43.36)
但是,请注意!我们正在描写一个平衡 条件,所以可以运用统计力学的平衡 定律。按照这些定律,在坐标x 处找到一个分子的概率正比于e -U/(kT) ,这里U 是势能。用数密度n a 表示,这意味着
n a =n 0 e-U / kT .(43.37)
将式(43.37)对x 求微商,得
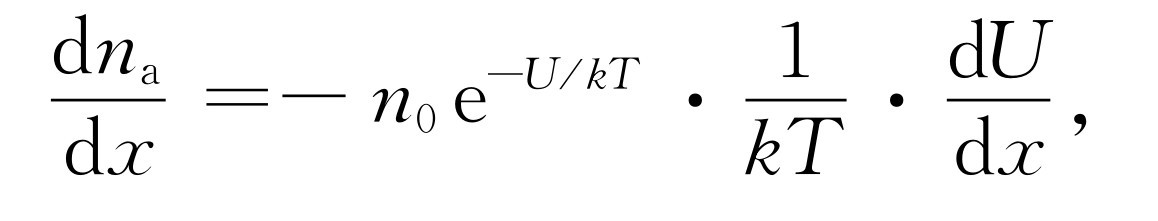 (43.38)
(43.38)
或
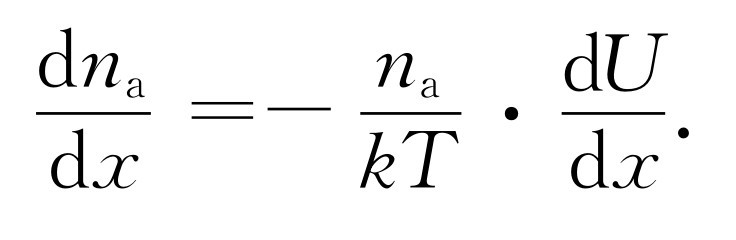 (43.39)
(43.39)
在我们的情况下,由于力 F 沿x 方向,势能U 正好是-Fx ,而-dU /dx =F 。由式(43.39)得出
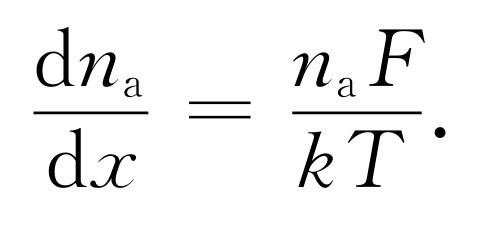 (43.40)
(43.40)
[这正是式(40.2),我们曾由它第一次推导出e-U / kT ,所以我们兜了一个圈子]!比较式(43.40)与(43.36),正好得出式(43.31)。这样,我们就证明了式(43.31)(它用迁移率 μ 给出扩散流)具有正确的而且是十分普遍的系数。迁移与扩散有着密切联系,这一联系首先是由爱因斯坦推得的。
§43-6 热导率
上面运用的分子动理论方法也可以用来计算气体的热导率 。如果某个容器顶部的气体比底部的气体热,热量将从顶部流到底部(我们假定顶部的气体较热,是因为否则将会形成对流现象,这样问题就不再是热传导 问题了)。热量由较热的气体向较冷的气体传递是由于带有较大能量的“热”分子往下扩散,以及“冷”分子往上扩散而引起的。为了计算热能流,我们可以问:通过面积元向下运动的分子带到下面的能量,以及通过这个面积向上运动的分子带到上面的能量是多少。它们的差就是向下的净能流。
热导率κ 定义为单位时间内通过单位面积的热能与温度梯度之比
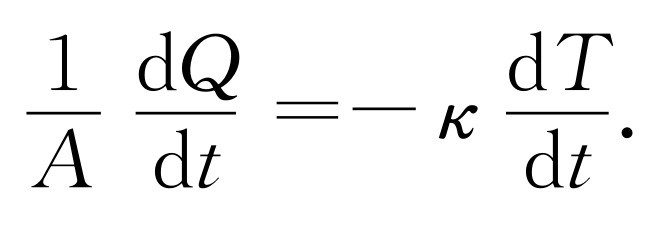 (43.41)
(43.41)
由于具体的计算十分类似于我们前面在考虑离子气体中的电流时 [1] 所作的计算,因此我们把证明
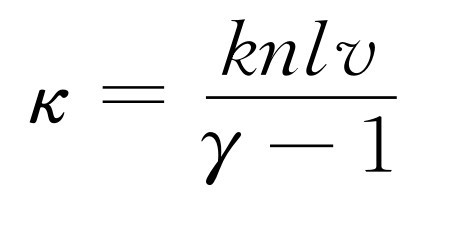 (43.42)
(43.42)
留给读者作为一个练习。(γ -1)kT 是一个分子在温度T 时的平均能量。
如果我们利用关系式nlσ c =1,热导率κ 可以写为
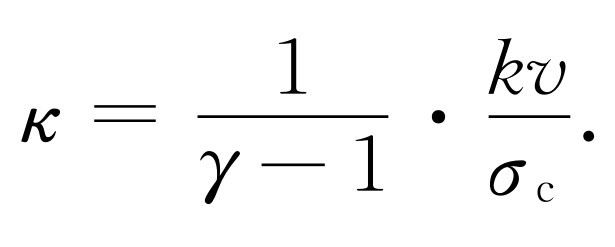 (43.43)
(43.43)
这是一个十分惊人的结果。我们知道,气体分子的平均速度与温度有关,而与密度无关 。我们期望σ c 只与分子的大小 有关,这样上面那个简单的结果表明热导率κ (因此也就是在任何特定情况下的热流率 )与气体的密度 无关!由于密度变化而带来的能量“载流子”数目的变化正好被两次碰撞之间载流子跑过的较长的距离所抵消。
有人会问:“在气体密度趋向于零的极限情况下,热流是否也和气体密度无关?如果这里根本没有气体呢?”当然不会!式(43.43)的推导和本章中的所有其他推导一样,是建立在碰撞之间的平均自由程远小于容器的任何尺度这个假设之上的。只要气体密度低到这种程度,使得一个分子有充分机会无碰撞地从容器的一个器壁跑到另一个器壁,本章的所有计算就都不能用。在这种情况下,我们必须回到分子动理论上去,重新计算将会出现的具体情况。