
当场随时间变化时,可通过给出场对时间的微商加以描述。我们希望用同样办法来描述场对位置的变化,因为对于例如在一点的温度与在邻近一点的温度间的关系,我们是感兴趣的。怎样求温度对位置的微商呢?我们求温度对x的微商吗?还是对y,或是对z?
有用的物理定律应当不依赖于坐标系的取向。因此,它们应被写成两边都是标量或两边都是矢量的一种形式。一个标量场的微商,比如说∂T/∂x,究竟是什么呢?是标量、矢量,还是其他什么东西?它既不是标量,也不是矢量,因为正如你能容易领会的,假如我们取不同的x轴,∂T/∂x肯定会不同。可是要注意,微商可能有三个:∂T/∂x,∂T/∂y和∂T/∂z。由于有这三个微商,而我们又知道要形成一矢量需要三个数,也许这三个微商就是一个矢量的分量:

当然,一般并非任何 三个数都能构成为一矢量。只有当我们旋转坐标系,矢量的各个分量按照正确的方式变换时,这才成立。所以需要分析坐标系旋转时,这些微商究竟是如何变换的。我们将证明式(2.11)确实是一个矢量。当坐标系转动时,这些微商的确按正确的方式变换。
我们可用几种方法来看这个问题。一个方法是,提一个答案与坐标系无关的问题,并尝试用“不变量”的形式来表示这一答案。例如,若S=A·B,而且若A和B都是矢量,则我们知道——因为我们已在第1卷第11章中加以证明——S是一个标量。无需研究它是否会随坐标系改变而改变,我们就已知道 S是一个标量,因为它是两个矢量的标积,所以它不可能 改变。与此相仿,如果我们有三个数B1 ,B2 ,B3 ,并且对每一个 矢量A都能找出
Ax B1 +Ay B2 +Az B3 =S, (2.12)
式中S对于任何坐标系都相同。那么,这三个数B1 ,B2 ,B3 必定 是某一矢量B的分量Bx ,By ,Bz 。
现在让我们考虑温度场。假设取P1 和P2 两点,它们分开一小间距ΔR。P1 处的温度为T1 而P2 处的为T2 ,彼此间的差ΔT=T2 -T1 。在这些实际的物理点,温度肯定与为测量其坐标而选取的各坐标轴无关。尤其是,ΔT为一个与坐标系无关的数值。所以它是一个标量。
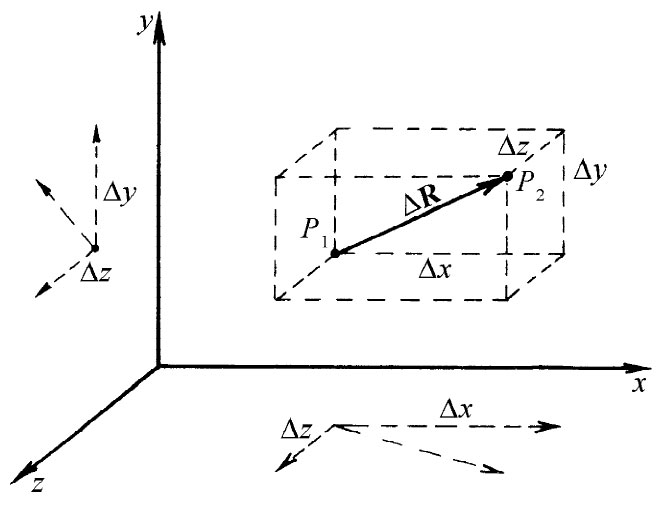
图2-5 矢量ΔR,其分量为Δx,Δy和Δz
如果我们选取一组方便的坐标轴,则能写出T1 =T(x,y,z)和T2 =T(x+Δx,y+Δy,z+Δz),其中Δx,Δy和Δz是矢量ΔR的分量(图2-5)。记住式(2.7),我们便可以写出:
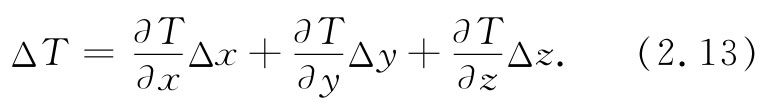
式(2.13)的左边是一个标量。右边是各含有Δx,Δy和Δz(一个矢量的分量)的三个乘积之和。这样我们得出结论,这三个数值
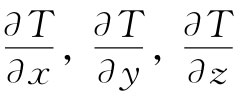
也是一矢量的x,y和z分量。我们用符号▽T描写这个新矢量。这个符号▽是Δ的颠倒,这会使我们回忆起微分来。人们用各种不同方式来读▽T:“del-T”,或“T的梯度”,或“grad T”,
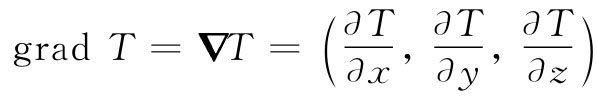 [1]
. (2.14)
[1]
. (2.14)
利用这个符号,可以把式(2.13)重写成一个更简洁的形式:
ΔT=T·ΔR. (2.15)
口头上这个式子说,两邻近点之间的温度差等于T的梯度与两点间位移矢量的点积。式(2.15)的形式也清楚地说明了上面我们关于▽T确是一个矢量的证明。
也许你还未相信吧!让我们用另一种办法来证明它(不过,如果你仔细加以考察,你可能会看到这实际上是兜一个更大圈子的同一种证法)。我们将证明,▽T的分量会按照与R的分量完全相同的方式变换。如果它们的确是这样,则按照第1卷第11章里我们关于矢量的原来定义,▽T就是一矢量。试取一个新坐标系x′,y′,z′,并用这一新系统算出∂T/∂x′,∂T/∂y′和∂T/∂z′。为了使事情稍微简单些,我们令z=z′,以便可以忘记z坐标。你尽可以自己检验更普遍的情况。
我们取一个相对于xy系转过角度θ的x′y′系,如图2-6(a)所示。对于点(x,y),在加撇系统中其坐标为:
x′=xcosθ+ysinθ; (2.16)
y′=-xsinθ+ycosθ. (2.17)
或者,解出x和y,则得:
x=x′cosθ-y′sinθ; (2.18)
y=x′sinθ+y′cosθ. (2.19)
如果任何一对数字在用这些方程进行变换时,其方式与x和y的变换方式一样,那么它们便是一个矢量的分量。
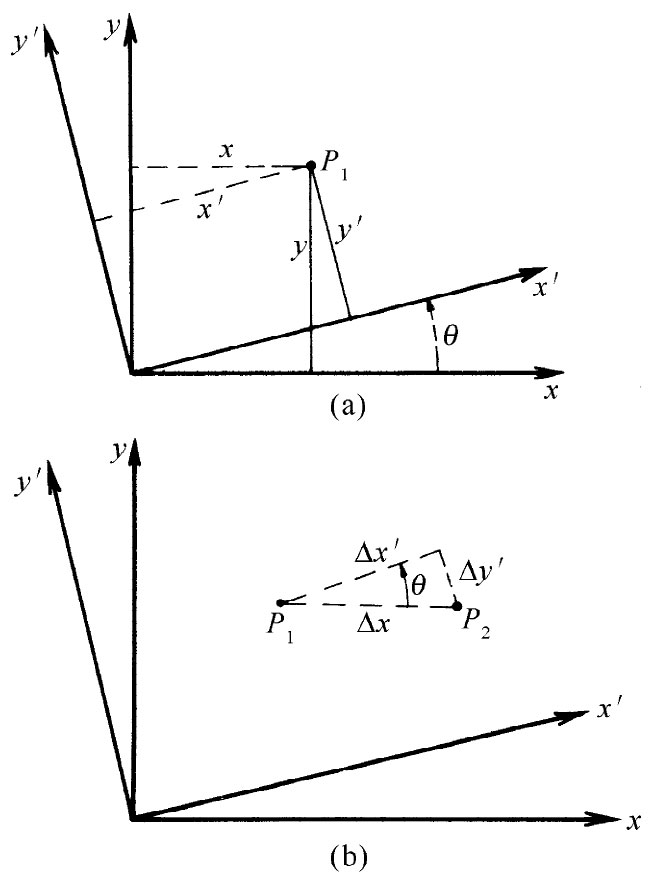
图2-6 (a)变换到一个已转动了的坐标系上去;(b)间距ΔR与x轴平行的一个特殊情况
现在让我们来看看如图2-6(b)所选取的两个邻近点P1 和P2 的温度差。若我们用x和y坐标来计算,则可以写成

因为Δy等于零。
在那个加撇的系统里进行计算,会得出个什么呢?我们应写成

看一看图2-6(b),即可知道
Δx′=Δxcosθ (2.22)
和 Δy′=-Δxsinθ, (2.23)
因为Δx为正时Δy′为负。把这些代入式(2.21),得:
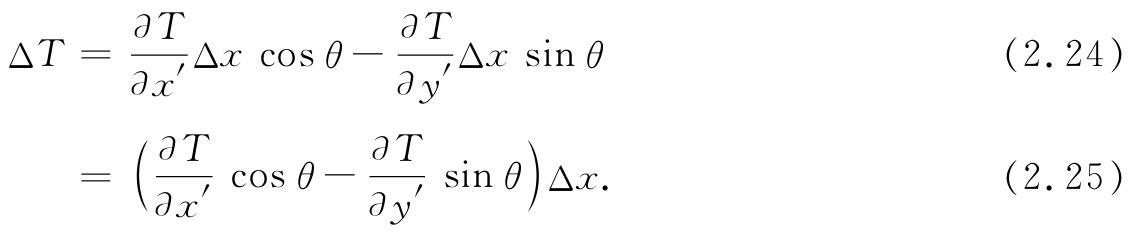
比较式(2.25)和(2.20),我们看到
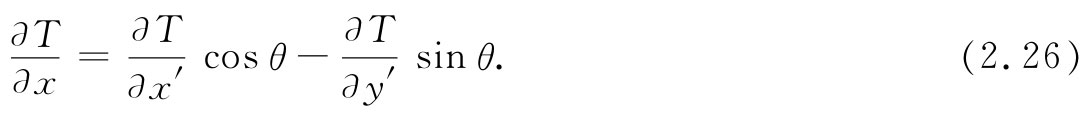
这个式说明:∂T/∂x可从∂T/∂x′和∂T/∂y′获得,正如同式(2.18)中的x可以从x′和y′获得那样。因此∂T/∂x就是一个矢量的x分量。同样的论据也可以证明,∂T/∂y和∂T/∂z分别为一个矢量的y和z分量。所以▽T肯定是一个矢量,它是从标量场T导出的一个矢量场。