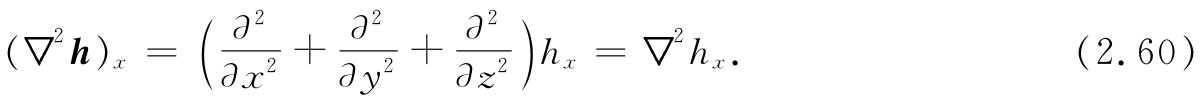
我们正在把关于一般矢量代数的知识应用到算符▽的代数上来,可是必须当心,因为有可能误入歧途。存在两个即将提到的陷阱,虽然它们并不会出现于本课程中。对于含有两个标量函数ψ和ϕ的下列表示式:
(▽ψ)×(▽ϕ),
你该说些什么呢?你也许会说:它必然等于零,因为它恰巧像
(Aa)×(Ab),
而两个相同 矢量的叉积始终是零。但是在这个例子中两个算符▽却不相同!前一个算符作用于函数ψ上;而另一个则作用于一个不同的函数ϕ上。所以尽管所用的是同一个符号▽,但它们仍应被认为是不同的算符。很明显,▽ψ的方向取决于函数ψ,因而它不大可能平行于▽ϕ。因此,
(▽ψ)×(▽ϕ)≠0 (一般地).
幸而,我们今后无需用到这些表示式(刚才所说的不会改变这么一个事实,即对于任一标量场ψ,▽×▽ψ=0,因为这里两个▽是对同一函数的作用)。
第二号陷阱(在这门课程中我们没有必要去研究它)如下:当应用直角坐标系时这里提出的法则既简单而又美妙。比方,若有了▽2 h,而希望获得它的x分量,那便是
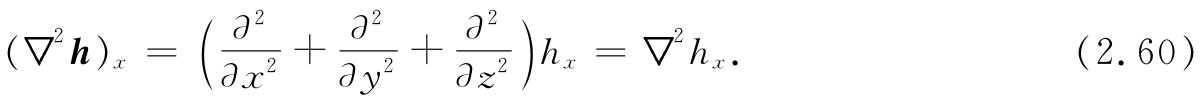
但如果我们所要求的是▽2 h的径向 分量,则这同一个表式就不 行了。▽2 h的径向分量并不等于▽2 hr 。原因是,如果我们同矢量代数打交道,矢量的方向就都是十分确定的。但当我们与矢量场打交道时,它们的方向则处处不同。如果我们试图用(比如说)极坐标来描述一个矢量场,则称为“径向”的那个方向便会逐点不同。因此,当我们开始对它的分量进行微分时,就会陷入一大堆麻烦之中。例如,甚至对一恒定不变 的矢量场,它的径向分量仍然逐点变化。
坚持只用直角坐标系往往是最保险和最简单的做法,而且避免了麻烦,但有一个例外值得一提:由于拉普拉斯算符▽2 是一个标量,所以我们就可能在我们想要的任意坐标系(例如在极坐标系)中把它写出来;但由于它是一个微分算符,所以只可以把它用到其分量各保持在固定方向上——即在直角坐标上——的那些矢量。因此,当我们用分量来写出矢量微分方程时,就必须把矢量场全部用它们的x,y,z分量来表达。
[1] 在我们的符号中,表示式(a,b,c)代表一个具有分量a,b和c的矢量。如果你喜欢用单位矢量i,j和k的话,那么可以写成:
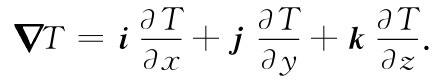
[2] 我们把h设想成一个取决于空间位置的物理量 ,而不是把它设想成一个严格的含有三个变量的数学函数。当h对于x,y,z或对于x′,y′,z′求微商时,h的数学表达式就必须先表示为合适的变量的函数。