
矢量算符▽,能否用作其他方面的代数运算?让我们尝试把它同一个矢量组合起来。可以通过点积来组合两个矢量,这可构成这样两种点积:
(矢量)·▽;或▽·(矢量).
第一种还没有什么意义,因为它仍然是一个算符。最终的含意取决于它所运算的对象如何。第二种乘积则是某个标量场(A·B总是一个标量)。
让我们就用一个已知的矢量场、比如h,来试试它与▽的点积吧。把它写成分量为:
▽·h=▽x hx +▽y hy +▽z hz (2.32)
或

这个和式在坐标变换之下是不变的。假如我们选择一个不同的坐标系(通过加撇来表明),则我们会有 [2]
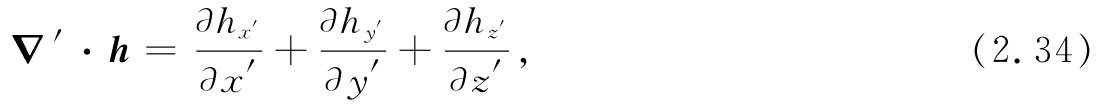
上式与式(2.33)尽管看起来不同,但所得的值相同 。这就是说,对于在空间每一点,
▽′·h=▽·h. (2.35)
因此,▽·h是一个标量场,它必定代表某个物理量。你会认识到,在▽·h中,各微商的组合方式相当特殊。此外,还有许多像∂hy /∂x的其他各种组合,它们既不是标量,也不是矢量的分量。
标量▽·(矢量)在物理学中非常有用。它的名称叫做散度 。例如,
▽·h=divh=“h的散度”. (2.36)
就像在上面对▽T所做的那样,也可以赋予▽·h一个物理意义。然而,我们将把这项工作推迟到以后。
首先,我们希望看看,由矢量算符▽是否还能设计些别的什么。我们必然指望
▽×h=一个矢量. (2.37)
它是一个矢量,其分量可按照有关叉积的通常规则[参见式(2.2)]写出:
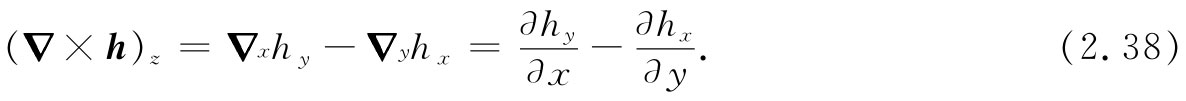
同理,
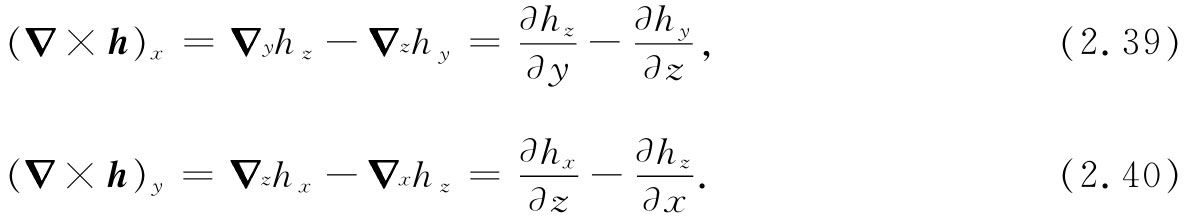
组合▽×h称为“h的旋度 ”,其命名原因及物理意义都将在以后讨论。综上所述,同▽的组合有三种:
▽T=gradT=矢量;
▽·h=divh=标量;
▽×h=curlh=矢量.
利用这些组合,我们可以用一种常规的方法——一种并不依赖于任何特定坐标系的普遍方法——来写出关于场的空间变化。
作为对矢量微分算符▽应用的一个例子,我们写出一组矢量方程,它们包含着我们在第1章中口头上给出的相同的电磁学定律,它们被称为麦克斯韦方程组。
麦克斯韦方程组 :
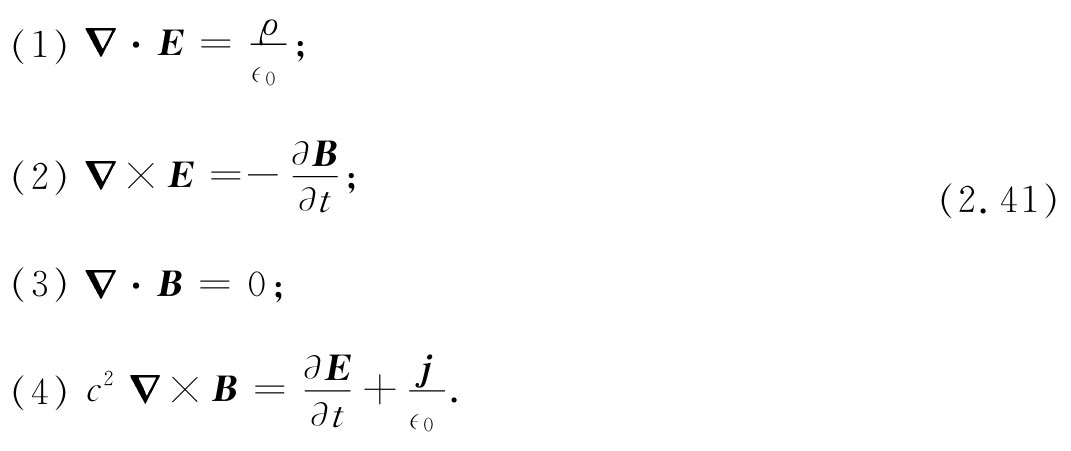
式中,ρ为“电荷密度”,即单位体积的电量;j为“电流密度”,即每秒通过单位面积的电荷流。这四个方程式包含了电磁场完整的经典理论。你们看到,采用这种新符号,我们可能得到多么优美而又简洁的形式!