
在本章中,我们将继续讨论与恒定电流有关的磁场——静磁学课题。磁场与电流之间由如下的基本方程相联系:

现在我们希望以一种普遍的方式,即不需要任何特殊对称性或直观猜测,就能在数学上解出这些方程。在静电学中,我们曾发现当所有电荷的位置均为已知时存在求场的一种直接方法。人们通过对电荷取积分——比如式(4.25)中的积分——就能简单地算出标势ϕ来。然后,如果还想知道电场,则可对ϕ求微商而得到。现在我们要证明:如果已知所有运动电荷的电流密度j,则会有一种求得磁场B的相应方法。
在静电学中,我们就知道(由于E的旋度始终是零),有可能把E表达成一个标量场ϕ的梯度。现在B的旋度却不 常等于零,因而一般说来不可能把它表达成一梯度。然而,B的散度 却永远为零,这就意味着我们总能把B表达成另一个矢量场的旋度 。因为正如我们以前曾在§2-7中见到的,旋度的散度总等于零。于是,就总能够把B与将被称作A的场互相联系起来,
B=▽×A. (14.3)
或者通过写成分量,则有
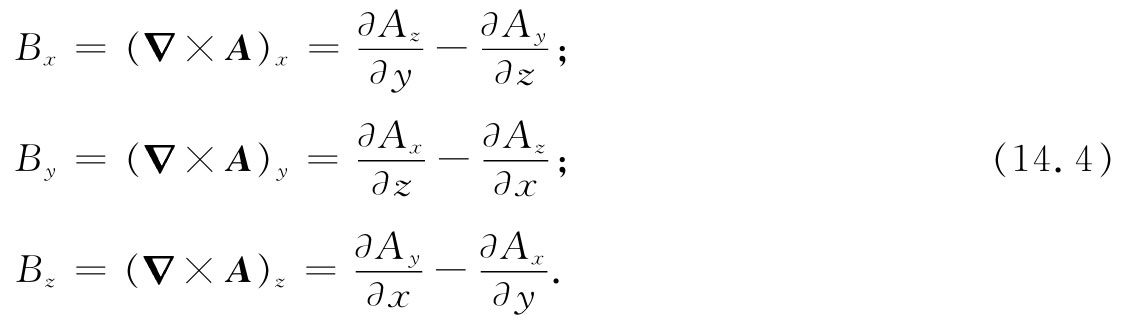
既然写出了B=▽×A,就能保证式(14.1)被满足,因为必然有
▽·B=▽·(▽×A)=0.
A这个场被称为矢势 。
你会记得,标势ϕ并未由其定义完全规定。如果你对某一问题已求得了ϕ,你还总能通过加上一常数而找到另一个同样好的势ϕ′:
ϕ′=ϕ+C.
因为梯度▽C为零,所以这个新的势ϕ′会给出相同的电场。因而ϕ′与ϕ代表相同的物理性质。
同样,我们也有可能给出同一磁场的不同矢势A。而且,由于B是由A的微商得到的,因而,若在A上加一常数并不改变任何物理的实质。可是对于A来说,还有更加广阔的活动余地。我们可以对A加进任何场,只要它等于某一标量场的梯度,就不致改变其物理情况。这可证明如下。假设对某个实际问题我们已有了一个A,它正确地给出了磁场B,并试问在什么情况下某一个新的矢势A′才能在代入式(14.3)中时,会给出同一个场 B。于是,A和A′必定具有相同的旋度:
B=▽×A′=▽×A.
因此, ▽×A′-▽×A=▽×(A′-A)=0.
但若一矢量的旋度为零,则它必然是某一标量场——比如说ψ——的梯度,因而A′-A=▽ψ。这就意味着,若A为适合于某一问题的矢势,则不论对于任何ψ,
A′=A+▽ψ (14.5)
仍将是一个同样令人满意的矢势,因为它导致相同的场B。
这样做往往很方便,即任意使A受另一条件限制,因而将其某些“活动范围”扣除出去(正如我们经常选取在无限远处的标势ϕ等于零也很方便一样)。例如,可以任意规定A的散度必须是什么而对A加以限制。我们总能够这样做,而不致影响B。这是因为:虽然A′和A都具有同一旋度,从而给出了相同的B,但它们却不需要具有相同的散度。事实上,▽·A′=▽·A+▽2 ψ,因而通过选取某一适当的ψ,就可以使▽·A′成为我们所希望要的任何东西。
对于▽·A到底应该如何选取呢?这一选择应为获得最大的数学方便而做出,并将取决于我们所要解决的问题。对于静磁学 来说,我们将做这种简单选择:
▽·A=0 (14.6)
(往后,当考虑电动力学时。将改变这种选择)。于是,目前我们对A的完整定义 [1] 为:
▽×A=B 和 ▽·A=0.
为了对矢势得到一些经验,让我们首先看看对于匀强磁场B0 来说,它的矢势是什么。选取z轴作为B0 的方向,我们就应有:
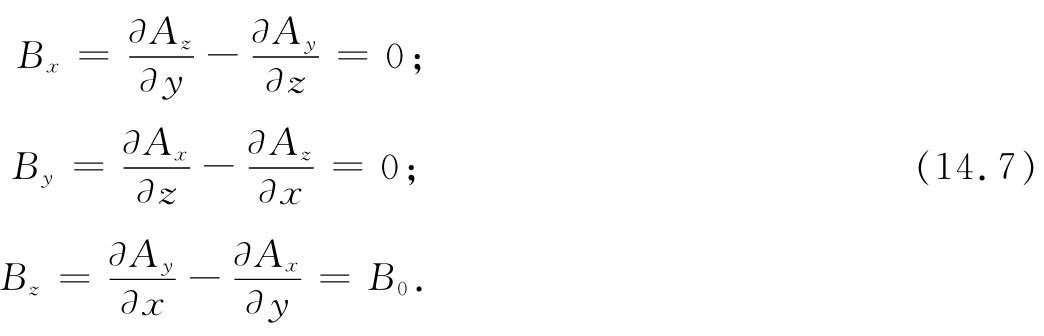
经检查可知这些方程的一个可能解为:
Ay =xB0 ; Ax =0; Az =0.
或者,我们也同样可以取:
Ax =-yB0 ; Ay =0; Az =0.
还有另一个解则是上述两个解的线性组合:
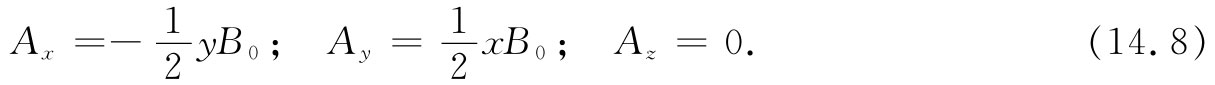
很明显,对于任一特定场B来说,矢势A有许多可能性,因而不是唯一的。
上面第三个解,即式(14.8),具有某些有趣的特性。由于其x分量正比于-y,而其y分量正比于+x,所以A必定垂直于与z轴同方向的矢量。我们把这个矢量叫作r′(之所以加上一撇是为了要提醒我们,并不是
从原点出发的一个位移矢量)。并且,A的大小仍正比于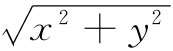 ,因而也就正比于r′。所以(对于我们的匀强磁场来说)A可以简单写成
,因而也就正比于r′。所以(对于我们的匀强磁场来说)A可以简单写成
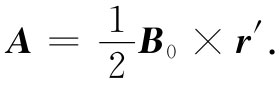 (14.9)
(14.9)
这矢势A具有B0 r′/2的量值并绕着z轴旋转,如图14-1所示。例如,若B场为螺线管内的轴向磁场,则这个矢势便和螺线管上的电流一样沿着同一指向环行。
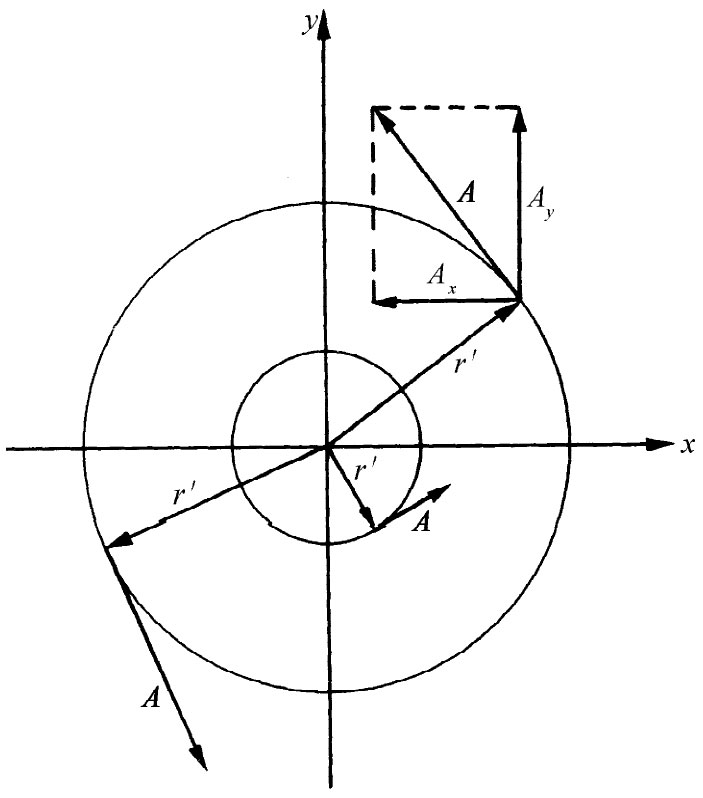
图14-1 一个沿z方向的匀强磁场B对应于绕着z轴旋转而又具有大小为A=Br′/2的矢势A(r′是从z轴出发的位移)
关于一匀强场的矢势也可由另一种方式获得。A绕任一闭合回路Γ的环流与▽×A的面积分可以由斯托克斯定理、即式(3.38)相联系:
∮Γ A·ds=∫在Γ内 (▽×A)·nda. (14.10)
但右边的积分等于B穿过回路的通量,因而
∮Γ A·ds=∫在Γ内 B·nda. (14.11)
因此,A绕任一 回路的环流等于B穿过该回路的通量。如果在与匀强场B垂直的平面上取一半径为r′的圆形回路,则通量恰恰为
πr′2 B.
如果把原点选取在对称轴上,则可以认为A沿着圆周并且仅仅是r′的函数,所以A的环流将为
∮A·ds=2πr′A=πr′2 B.
同上面一样,我们得到
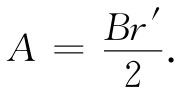
在刚才所述的例子中,我们已从磁场算出了矢势,这与正常做法恰好相反。在复杂问题中,往往先解得矢势,然后才由它来确定磁场,那就比较容易。接下来,我们将说明如何才能做到这一点。