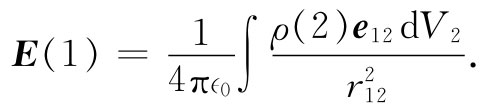
在学习静电学时我们了解到,某一已知电荷分布的电场可直接由积分式(4.16)获得:
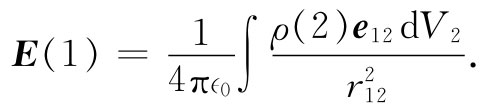
正如我们曾经见到的,要算出这一积分——实际上是三个积分,每一分量各有一个——比起算出势的积分并求出它的梯度来,通常要花费更多工夫。
有一个相似的积分,它把磁场同电流联系了起来。我们已有一个关于A的积分,即式(14.19),就可以通过对该式两边取旋度而获得关于B的积分:
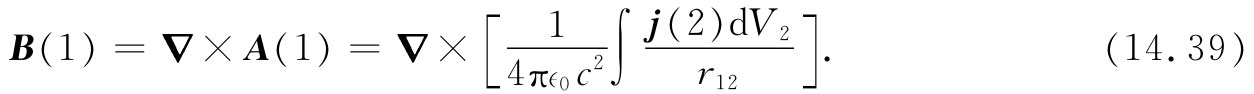
现在我们必须小心:该旋度算符的含义是取A(1)的旋度,这就是说,它仅对坐标(x1 ,y1 ,z1 )进行运算。如果我们记住,▽×这个算符只对附有脚标1的那些变量才进行运算,而这些变量显然仅出现于
r12 =[(x1 -x2 )2 +(y1 -y2 )2 +(z1 -z2 )2 ]1/2 (14.40)
中,则可将该算符移进积分符号之内。对于B的x分量,我们得
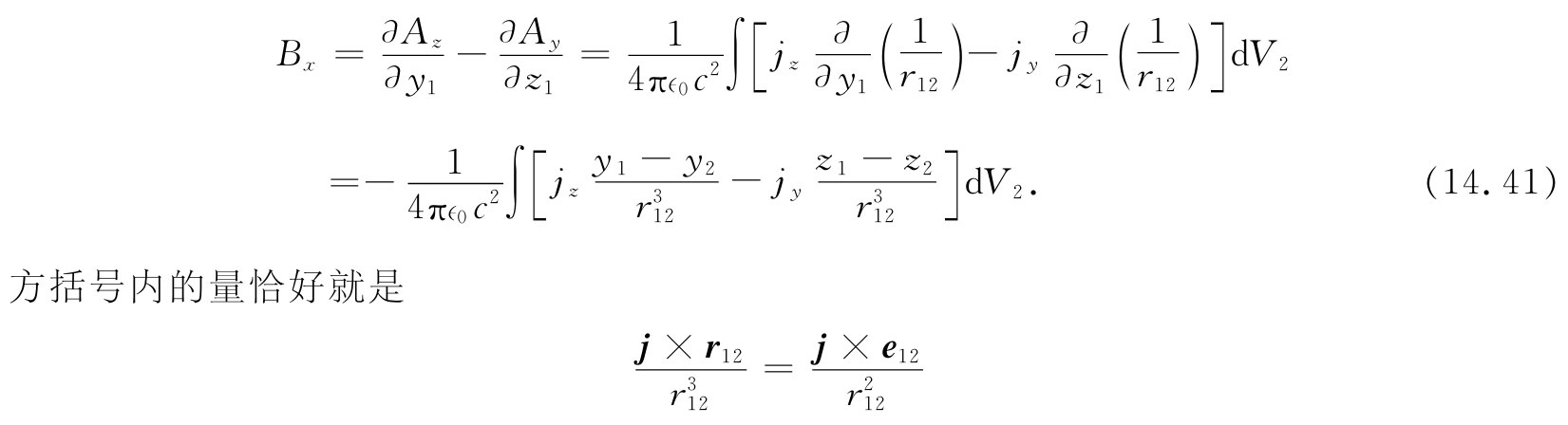
的x分量。对于其他分量,我们将会找出相应结果,因而有
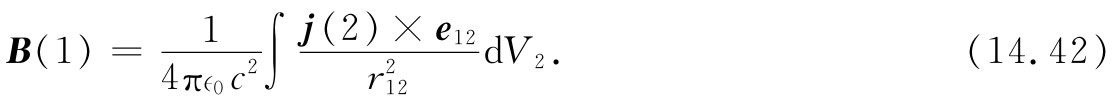
这一积分直接由已知的电流给出了B。这里所涉及的几何性质与图14-2中所示的相同。
若电流仅存在于细小导线的电路中,则如同上一节,我们可立即从导线的一头到另一头加以积分,即用Ids代替jdV,其中ds是导线的长度元。这时,采用图14-10上的符号,便得:
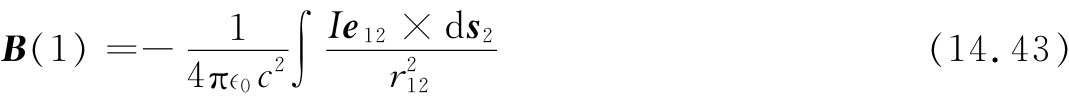
(负号之所以出现是由于我们颠倒了该叉积的次序)。这一有关B的方程,以它的发现者的名字命名,称为毕奥 —萨伐尔定律 。它提供一个直接获得载流导线所产生的磁场的公式。
你可能会觉得奇怪:“如果能直接由那个矢量积分找出B来,则矢势还有什么用处呢?毕竟A也含有三个积分!”因为有关B的积分中存在叉积,所以该积分往往较为复杂,正如由式(14.41)显然可见。并且,由于A的积分同静电学的那些相仿,所以我们可能已经懂得它们了。最后,我们还将见到:在更高一级的理论内容(比如相对论,力学定律的更高级描述方式,像以后将要讨论到的最小作用量原理,以及量子力学等)中,矢势起着重要的作用。
[1] 我们的定义仍未唯一地确定A。对于一个唯一 的规定,我们还得说明在某个边界上或在无限远处场A的行为如何。例如,选取在无限远处场趋向于零有时是方便的。