图 19-1
当我在中学念书时，我的物理教师——他的名字是巴德（Bader）先生——有一次在讲完了物理课之后，把我叫住说：“看来你有点厌烦，我要给你讲点有趣的东西。”然后，他告诉我一件事，我发现它是绝对会令人神往的，并且自那时以来，我发现它总是那么引人入胜。每次提出这一课题时，我就会对它进行分析研究。事实上，当我开始准备这次演讲时，我发现自己对这个问题正在做更详尽的分析。并不是为这一次演讲操心，实则我已被卷入到一个新的问题中去了。这个课题就是——最小作用量原理。
巴德先生这样告诉我：假定有一质点（例如，在一引力场中）通过自由运动从某处移动至另一处——你把它抛掷出去，它就会上升而又落下［图19-1（a）］。它在一定时间内由出发点到达最后的地方。现在，你尝试一个不同的运动。假设由这里到达那里是如图19-1（b）这样进行的，但所用时间却正好相同。然后他又这样说：如果你算出在该路径上每一时刻的动能，减去势能，再计算出在经历整条路径期间它对时间的积分，你将会发现所获得的数值比对实际运动所获得的要大 。
图 19-1
换句话说，牛顿定律可以不写成F=ma的形式而表述成：一物体从一点到另一点所走的路径其平均动能减去平均势能应尽可能地小。
让我把这里面的意义说得更清楚些。如果我们考虑引力场的情况，那么若粒子的路径为x（t）（让我们暂时只考虑一维，即是一条升高、降落、但绝不会偏斜的轨道），其中x是地面以上的高度，则在任一时刻动能为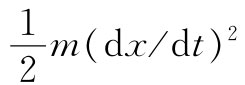
，而势能为mgx。现在我沿该路径在每一时刻取动能减去势能再对时间自始至终进行积分。假定在起始时刻t1
由某一高度出发，并在结束时刻t2
确实到达了另外某一点［图19-2（a）］。
那么该积分就是
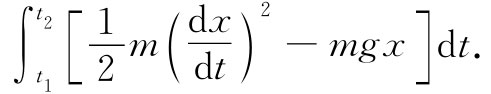
实际的运动为某种类型的一条曲线——如果作一个位置时间图，它是一条抛物线——而对于该积分会给出一个确定的值。但我们也可以设想 另一种运动，它升得很高，而且以某种特殊的方式上升和下落，如图19-2（b）所示。我们可以算出动能减去势能并对这么一个路径或其他任何我们所想要的路径积分。令人诧异的是，真正的路径就是那一条会使这一积分取得最小值的路径。
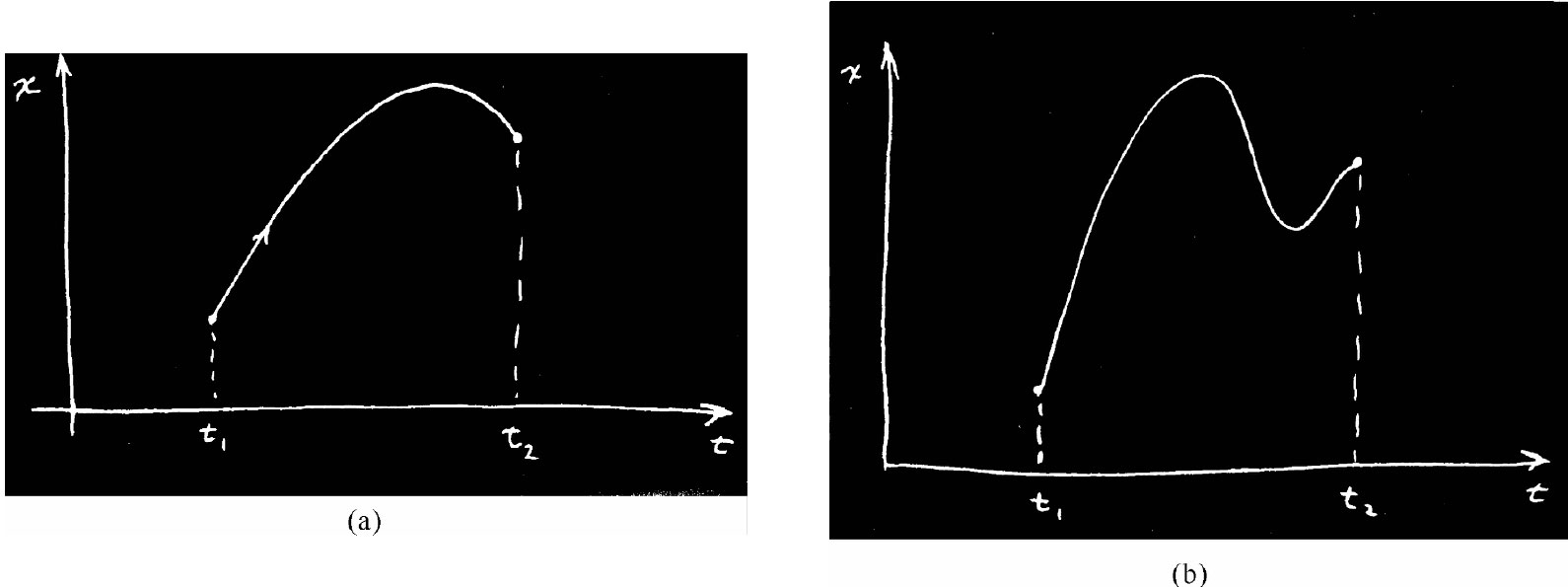
图 19-2
让我们把它们彻底检验一下。首先，假定取一个完全没有势能的自由质点的情况。那么，该法则讲：在给定时间内在从一点跑至另一点的过程中，动能的积分是最少的，因而它一定要以均匀的速率行进（我们知道这是一个正确答案——以匀速率前进）。为什么是这样呢？因为假如该质点以任何其他方式运动，则其速度将有时比平均值高，有时比平均值低。因为它一定要在给定的时间内由“这里”到达“那里”，所以平均速度对于每一情况都是相同的。
作为一个例子，比如你的任务是乘车在给定时间内从家里到达学校，你可以用几种方式做到这点：可以一开始就像疯子似的使车子加速，然后在接近终点时用刹车逐渐放慢速度；或者你可以匀速前进；甚至你也可向后走一会儿，然后再往前开，如此等等。事实是，平均速率当然必须是你所经过的总距离除以所用的时间。但如果你试用各种方式、但就是不以匀速前进，那么你总会有时太快而有时则太慢。如你所知，围绕平均值偏差的某事件，其均方 值恒大于其平均值的平方。所以如果你不保持开车的速度，那么动能的积分就总比用均匀速度开车时为高。所以我们看到，如果速度固定不变（当没有力作用时），则该积分便是一个极小值。正确的路径如图19-3这样。
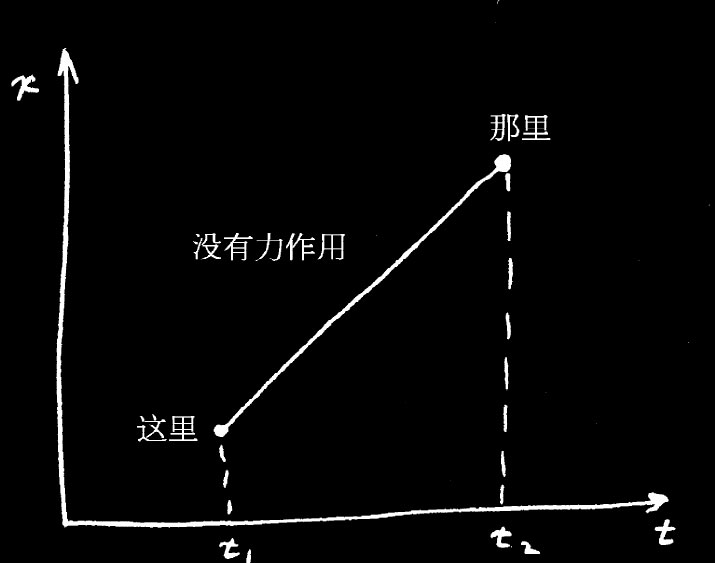
图 19-3
现在，一个在引力场中被上抛的物体起初升得较快，然后逐渐放慢。那是因为物体还具有势能，所以就平均而言必须有最小的动能与势能之差 。由于在空中上升时势能增大，所以如果我们能够尽快上升到高势能的地方，则将获得一个较低的差 值。这样该势能才能从动能那里扣除出去，从而获得较低的平均值。所以最好就是去选取能够升得高、从而可从势能处得到很多负值的那一条路径（图19-4）。
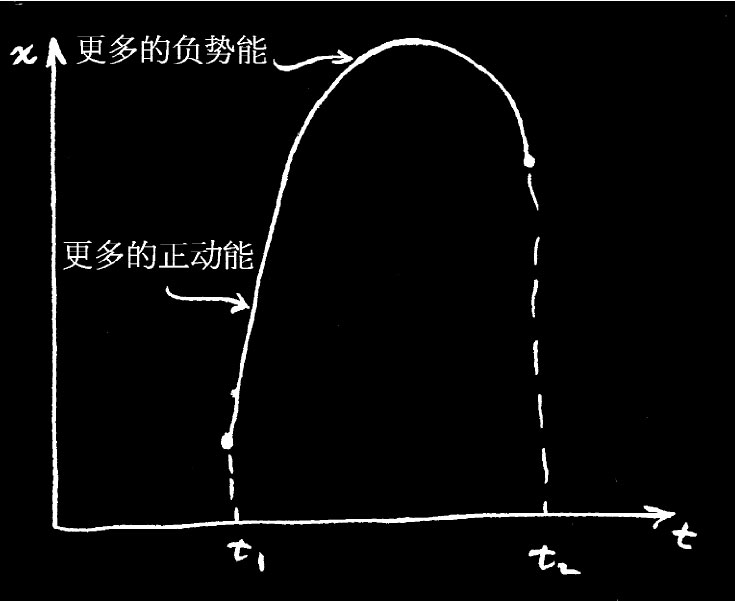
图 19-4
另一方面，你也不能够升得太快，或跑得太远，因为这么一来你将会包含过多的动能——你得很快达到高处以便在可利用的规定时间里再落下来。所以你也不宜升得太高，但总要升到某个高度。因此事实证明，答案是在试图获得更多的势能与最少的额外动能之间取得某一种平衡——以期获得动能减去势能的差值尽可能小。
这就是我的老师告诉我的全部内容，因为他是一位十分好的教师并懂得在什么时候应停止对话。但我却还未懂得要在什么时候结束谈话，所以并不会留给你一个有趣评论，而我却想要来证明它确是如此，这无异用生活中的复杂性来使你感到不安和焦躁。我们将遇到的数学问题会十分困难，而且是一个崭新的课题。我们有某一个叫作作用量 S的量。它是动能减去势能后对时间的积分。
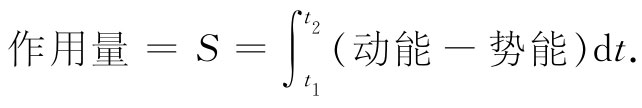
记住势能和动能两者都是时间的函数。对每条不同的可能路径你将获得有关这个作用量不同的值。我们的数学问题是找出使这个数值最小的那一条曲线。
你会说——呵，那不过是普通微积分学中的极大和极小问题罢了。在算出了作用量之后，只要求导就能找出那个极小值。
但是要小心。通常我们只有某变量的函数，而我们得求出使该函数为最小或最大的那个变量 值。例如，设我们有一根棒，在其中部已加了热，因而热量将向两边传送出去。对于棒上每一点都有一个温度，而我们必须找出温度最高的那一点。但现在对于空间每一条路径 我们有一个数值——完全不同的事件——而我们得找出那一条会使该数值极小的空间路径 。那是完全不同的一个数学分支。它并不是普通的微积分。事实上，它被称为变分学 。
有许多问题属于这一类数学。例如，圆周往往被定义为与一固定点的距离为常数的所有点的轨迹。但圆周还有另一种定义的方法：圆周是具有给定长度 而包围最大面积的那条曲线。对于给定周长来说，任何其他曲线所包围的面积都比圆周包围的要小。因此，若我们提出这样一个问题：试求给定周长而能包围最大面积的那条曲线，我们就会有一个变分学问题——与你们熟悉的有所不同的一种微积分。
这样，我们就对一物体的路径进行计算。这里介绍一下将用的方法。我们的意图是：设想一条正确的路径，以及画出任何其他都是错误的路径，因而若对错误路径算出作用量，则将得到一个比按正确路径算得的作用量要大的结果（图19-5）。
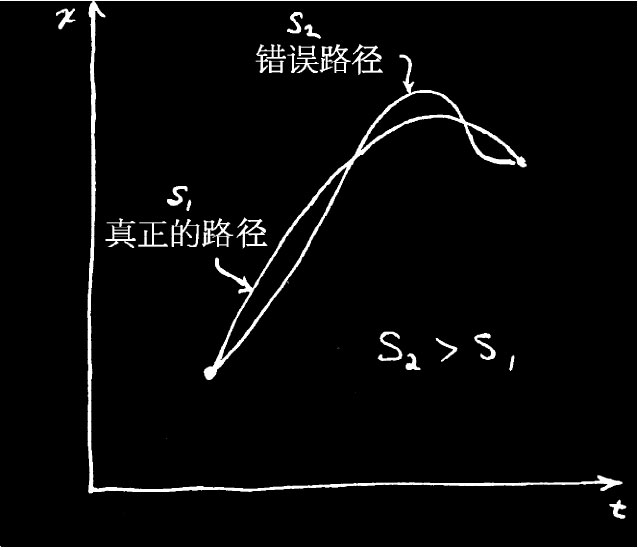
图 19-5
习题：试找出真实路径。它到底在哪里？当然，一种方法是去算出千千万万条路径上的作用量，再找出哪一条是最小的。当你找到了那条最小的时，它就是正确的路径了。
那是一种可能途径，但我们却能够比这做得更好些。当有一个具有极小值的量——例如像温度那样的普通函数——时，极小值就有这么一个特点：若变量 偏离极小值位置为一级小量 ，则函数与极小值的偏差仅为二级小量 。在该曲线的任何其他部分，若原位置移动一个小距离，则函数值也将改变一级小量。但在极小处，一个微小的偏离在一级近似下函数不产生差异（图19-6）。
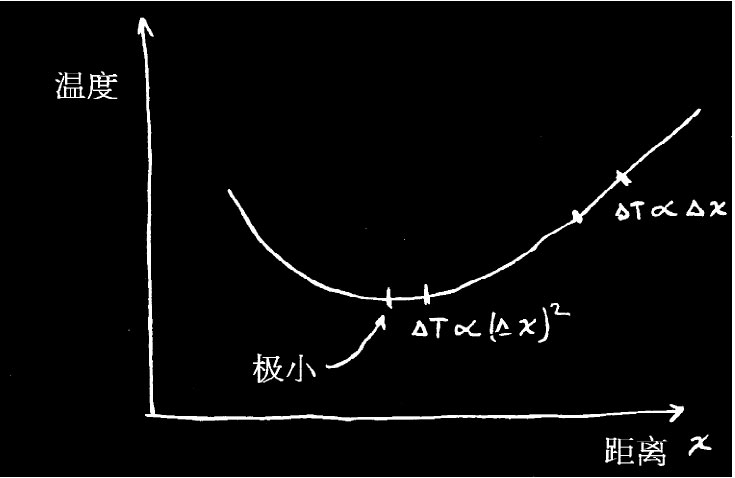
图 19-6
这就是我们将用来计算真实路径的办法。如果已有一条真实路径，那么一条与它只有微小差别的曲线，其作用量在一级近似下将不会造成什么差别。若确实有一个极小值的话，则任何差别都将在二级近似内。
那不难证明。若当我们使曲线偏离某个路径时发生一个一级小量的变化，则作用量就有一个与该偏离成正比 的变化。这变化大概会使作用量变得较大，否则我们就不会得到一个极小值了。但是若该变化与偏离成正比 ，则改变偏离的符号将会使作用量变得较小。我们将获得这样的作用量，沿一条路径它增加，而沿另一条路径它减少。作用量真正能够是极小值的唯一路径，是作用量在一级近似下不做任何改变的路径。而作用量的改变是与对真实路径偏离的平方成正比的。
所以我们就这样来做：称x（t） （下边加一底线）为真实路径——即我们试图要寻找的。取某条尝试路径x（t），与该真实路径有一微小差别，这差别我们称之为η（t），见图19-7。
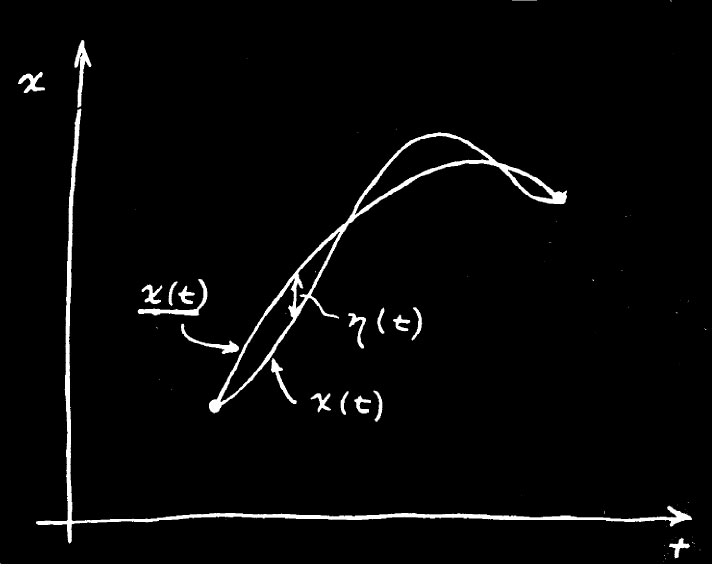
图 19-7
现在我们的想法是：若对路径x（t）计算作用量S，则这个S与我们对路径x（t） 所算出的作用量——为了简化写法，我们可叫它作S ——之差，即S与S 之差，在小η的一级近似下应等于零。这差可以是二级小量，但在一级近似下这差必须为零。
而这对于任何一个η都必定是正确的。噢，还未尽然。这方法不会具有任何意义，除非你所考虑的各路径彼此都有相同的起点和终点——每条路径都在t1 时刻从某点出发而在t2 时刻到达另一点，这些地点和时间都保持固定不变。因此，我们的偏离η在每一端都应等于零，即η（t1 ）=0和η（t2 ）=0。有了这个条件，我们的数学问题才告确定。
要是你完全不懂得微积分，为了求一普通函数f（x）的极小值你或许也是这样做。你可能会讨论如果对f（x）中的x加一小量h后会发生的情况，并论证以h的一次幂对f（x）的修正在极小值处必然等于零。你会以x+h取代x并展开至h的一次幂……正如我们将要对η做的那样。
于是我们的想法是，把x（t）=x（t） +η（t）代入作用量公式中，
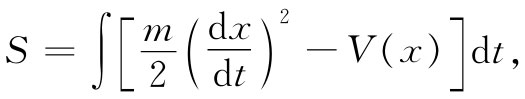
式中V（x）代表势能。而dx/dt这个微商当然就是x（t） 的微商再加上η（t）的微商，所以对于作用量我得到这个表达式：
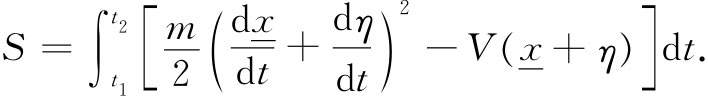
现在我必须写得更详尽些。对于该平方项得到
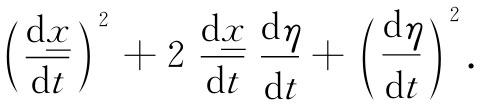
可是请等一等。对高于一次幂的项我并不在意，因而将所有含有η2 和更高次幂的项都取出来并放进一个标明“二次和更高次项”的小箱子中。从上式中的这一平方项我只得到二次幂，但从其他方面还可得到更多一些东西。因此，动能部分就是
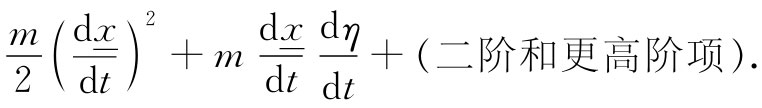
现在我们需要一个在x +η处的势能V。我认为η是小量，因而可以将V（x）写成泰勒级数。它近似地等于V（x ），在下一级近似下（按微商的通常性质）则该修正的应该是η乘以V对x的变化率，如此等等：
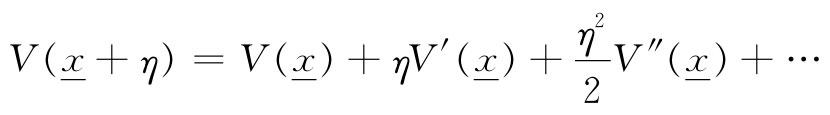
为了简化书写，我已将V对x的微商写成V′。至于η2 项以及其后面各项则都落在“二阶和更高阶项”的范畴之内，而我们便不需对之操心了。将所有这一切都合起来，得：
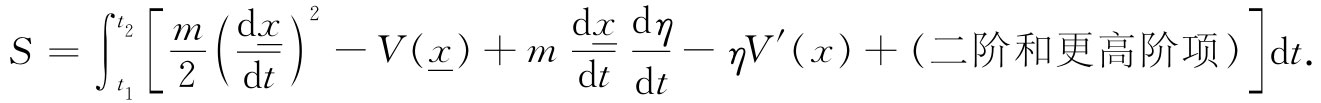
现在，如果我们对事情观察得仔细些，则会见到我在这里整理好的头两项相当于用真实路径x 应该计算出来的作用量S ，而我要集中注意力的东西乃是S的变化——S与对正确路径所应得的S 之间的差。我们把这差写成δS，并称之为S的变分。略去那些“二阶和更高阶项”，则对于δS得
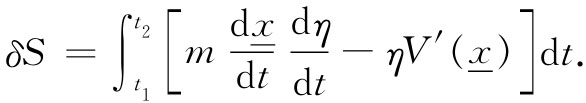
现在的问题是：这里是某个积分。虽然我还不知道x 是什么，但我确实知道不管η是什么 ，这一积分必须等于零。噢，你试想想，这件事可能发生的唯一办法就是乘上η的部分应当是零。可是含有dη/dt的第一项又怎么样呢？噢，归根到底，既然η可以是任何变量，它的微商也是任何变量，因而你可以断定dη/dt的系数也必定等于零。那样讲不完全正确。之所以不完全正确是因为η与它的微商之间存在着联系，它们并非完全独立，因为η（t）必须在t1 和t2 两个时刻都等于零。
在变分学中解决一切问题的方法总要用到相同的普遍原理。即首先对你所要变化的东西做一个移动（像我们上面通过加η而做到的那样），旨在寻找一级小量的项；然后 又总是把积分安排成含有“某种东西乘以移动（η）”的形式，而其中又不含有其他微商（没有dη/dt）。为此必须重新安排以便总是“某件东西”乘以η。过了一会你将会看出这样做的巨大价值（也有一些公式会告诉你，在某些情况下如何不经实际计算就能获得结果，但这样一些公式都不够普遍，所以就不值得你去关注；最好的办法还是按照上述这一种方法把它算出来）。
怎么才能将dη/dt项重新安排使其含有η呢？回答是通过分部积分就可以做到。事实证明，变分学的全部巧妙就在于先写下S的变分，然后利用分部积分使得η的微商消去。在微商会出现的每个问题中总是采取相同的办法。
你回忆一下分部积分的一般原理。如果你有任意函数f乘以dη/dt并对t积分，可以写下ηf的微商：
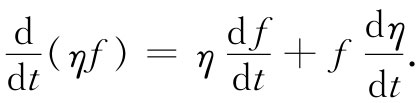
你所要的积分是对末一项而积的，因此，
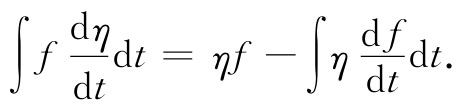
在我们关于δS的公式中，函数f就是m乘以dx /dt，因此，我得到下列关于δS的公式：
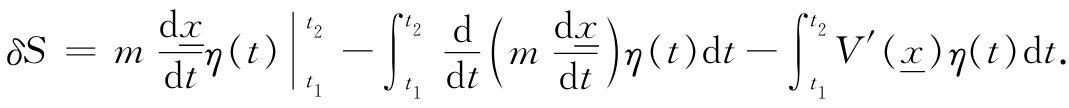
首项必须在t1 和t2 两个限上算出来。然后我还必须对那个从分部积分剩下来的部分积分。末项则是照抄下来的，没有什么改变。
现在碰到一件总会发生的事情——积出的部分不见了（事实上，如果该被积出的部分不消失，则你就应当重申该原理，并加上一些条件以确保其消失）。我们已经说过，在路径两端η必须是零，因为该原理要求只有在该变化曲线开始并终结于选定的点时作用量才是一极小值，这条件就是η（t1 ）=0和η（t2 ）=0，所以该项积分结果为零。我们将其他各项都集合起来并得到：
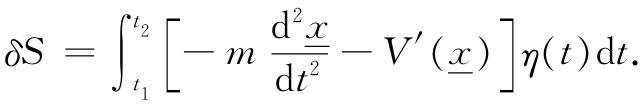
S的变分现在就成为我们所希望得到的形式了——在该方括号内的各项，比方说F，全都乘上了η（t）并从t1 积至t2 。
我们得到了某种东西乘以η（t）的积分总等于零：
∫F（t）η（t）dt=0.
这里我有t的某个函数，再以η（t）相乘，并从一端至另一端对它积分。而不论η是什么，结果始终为零。这意味着函数F（t）是零。尽管这很明显，但无论如何我会给你证明看看。
假设对于η（t），我选取除了某一特定t值外其余一切t上都等于零的某变量。在到达这个t前它始终保持零值（图19-8），在时刻t它突然跃起，过了一会又骤然降下。当我们对这个η乘以任意函数F做积分时，唯一不等于零的地方就是η（t）出现脉冲的地方，这时我们会得到在该处的F值乘以对脉冲的积分。对于脉冲本身的积分不会等于零，但当乘上了F之后它就必须等于零；所以函数F在脉冲处必然为零。但由于脉冲发生在我们想要它发生的任何地方，因而F就必须处处为零。
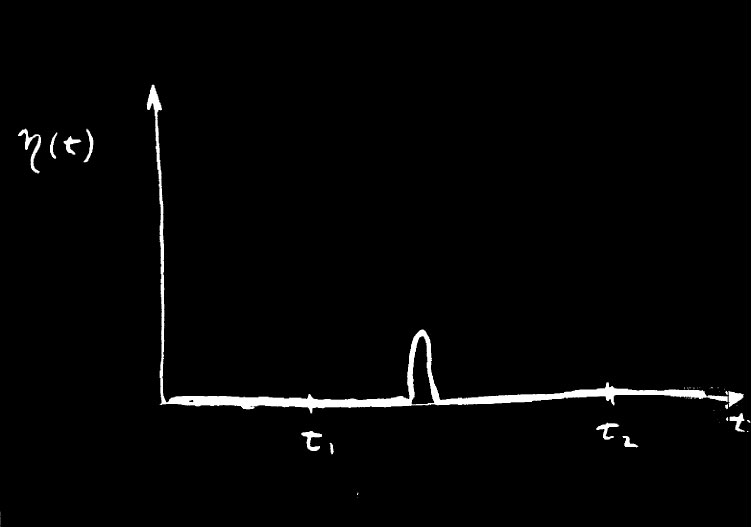
图 19-8
我们看到，如果对于任何η，我们的积分为零，则η的系数必须为零，只有满足这个复杂微分方程
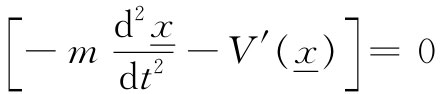
的那条路径，作用量积分才将是极小值。实则它并非那么复杂，你以前就见过这方程，它不过是F=ma罢了。第一项是质量乘加速度，而第二项则是势能的微商，那就是力。
所以，至少对于一个保守系统来说，我们已证明最小作用量原理给出了正确答案。它表明，具有最小作用量的那条路径就是满足牛顿定律的那条路径。
一个述评：我从未证明它是一个极小值 ——也许是一个极大值。事实上，它的确不必是一个极小值。这与我们过去在讨论光学时所发现的那个“最少时间原理”十分类似。在那里我们起初也曾说过是“最少”时间。然而事实却证明，会有时间并非最少 的一些情况。基本原理是，对于任何离开光学路径的一级变化 ，时间的变化 为零；情况与此完全一样。所谓“最小”我们实在是指，当你改变路径时，S值的一级变化为零。它未必是“极小”。
其次，我谈论一些推广的问题。第一，可以推广至三维，即不只是x，我可能有x，y和z作为t的函数，此时作用量更为复杂。对于三维运动，你必须用到完整的动能——（m/2）乘上整个速度的平方。这就是
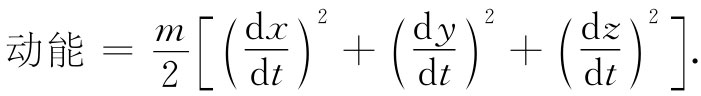
并且，势能也是x，y和z的函数。而路径究竟如何呢？路径是空间中某条一般的曲线，它很不容易画出来，但意思却是一样的。不过η又是怎么回事？噢，η可以有三个分量。你可以在x方向、y方向或z方向——也可以同时在所有三个方向移动路径，所以η应该是一个矢量。然而，这样做实际上并未把事情弄得过于复杂。由于只有一级 变分必须为零，我们便可以通过三个连续移动而进行计算。可仅仅在x方向移动η，而说明它的系数必须为零，这样就得到一个方程，然后在y方向移动而得到另一个方程，又在z方向得到第三个。当然，或者按照你所喜欢的任一种次序进行。无论如何，你得到了三个方程。而牛顿定律实际上就是在三维空间中的三个方程——对每一分量就有一个。我想你实际上能够明白，这是一定行得通的，但这个三维问题仍留给你自己去证明。顺便提一下，你也可以采用任一种你所喜欢的坐标系，诸如极坐标或其他坐标，通过观察你在半径、角度或其他坐标方向移动η时发生的事情，就会立即得出适用于该坐标系的牛顿定律。
同样，这一方法也可推广至任何数目的粒子。例如，如果你有两个粒子，而在它们之间有作用力，因而就有相互作用势能，那么你只要将这两粒子的动能相加并取它们间的相互作用能作为势能。对此你想要变化什么东西呢？势必变化双 粒子的路径。于是，对于在三维中运动的两个粒子，就总共有六个方程。你可以在x方向、y方向和z方向变更第一个粒子的位置，而对于第二个粒子也是这样做，因而就有六个方程。而这是理应如此的。其中三个方程确定了第一个粒子受力作用时的加速度，而另外三个则确定第二个粒子受力作用时的加速度。你继续坚持进行同样的游戏，就会得到关于任何数目的粒子在三维中的牛顿定律。
我刚才说过，我们得到了牛顿定律。这并非十分正确，因为牛顿定律还包括像摩擦一类非保守力。牛顿说ma等于任何F，可是最小作用量原理却只适用于保守 系——那里所有的力都可以从势函数获得。然而，你知道，在微观层次——即在物理学最深入的层次——并没有非保守力。像摩擦力那样的非保守力，之所以出现乃是由于我们忽略了微观上的复杂性——存在的粒子实在太多难于分析。但基本 定律却都可以 放进最小作用原理的形式之中。
让我继续来做进一步的推广。假定我们问起粒子做相对论性的运动时会发生什么情况，而上面还未获得正确的相对论性运动方程；F=ma只对于非相对论才正确。问题是：对于相对论性的情况是否有一个对应的最小作用量原理？回答是肯定的。对于相对论性情况其公式如下：
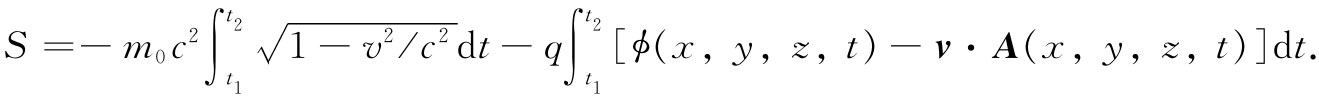
这个作用量积分的第一部分是粒子的静质量m0
乘以c2
再乘以对于速度函数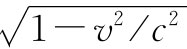
的积分。后一项不再是势能，却是一个对于标势ϕ和对于v乘以矢势A的积分。当然，此时我们只包括电磁力。所有的电场和磁场都是由ϕ和A提供的。这一个作用量函数对于单个粒子在电磁场中的相对论性运动给出完整的理论。
当然，每当我写出v时，你总会明白，在试图做出任何计算之前，得先用dx/dt来代替vx
，并对其他各分量也都这样做。而且，你还必须把沿路径在t时刻的一点写成x（t），y（t），z（t），而这些在上式中我只是简单地写作x，y，z。严格讲，只有当你已经对v等做了这种代换以后，你才能有一个关于相对论性粒子的作用量公式。事实上这个作用量公式确能给出那些正确的相对论性运动方程，我将把这一问题的证明留给你们中那些较机敏的人去做。我是否可建议你们先做没有A、亦即没有磁场的情况？此时你应当得到运动方程dp/dt=-q▽ϕ的各分量，其中你会记起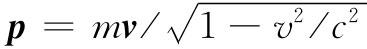
.
把存在矢势的情况也包括进去就困难多了。那些变分变得相当复杂。可是最终，解得的力项确实为q（E+v×B），正该如此。但我将把这留给你们去考虑。
我想要强调，在一般情况下，比如在相对论公式中，那作用量的被积函数不再具有动能减去势能的形式。那是只有在非相对论性的近似下才正确的。例如，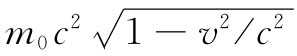
这一项就不是我们所称的动能了。对于在任何特定情况下作用量应该是什么的问题必须通过某种试试改改的办法来确定。这与首先确定什么是运动定律的问题恰好相同。你只要对所已知的一些方程反复尝试，就看出你能否把它们纳入最小作用量的形式之中。
还有一点是关于名称方面的。那个经过对时间积分就可以得到作用量S的函数称为拉格朗日函数
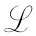，它只是粒子的速度和位置的函数。因此最小作用原理也就可以写成
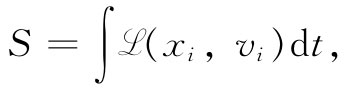
其中xi 和vi 指位置和速度的所有分量。所以如果你听到有人正在谈论“拉氏函数”，你就会知道他们是在谈论那个要用来求出S的函数。对于在电磁场中的相对论性运动，
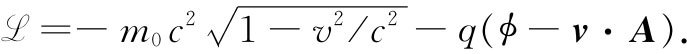
并且，我还应该讲，对于大多数讲究准确和学究式的人物来说，S实际上并非叫作“作用量”，它称为“哈密顿第一主函数”。现在，我讨厌的是，要来做一次关于“最小哈密顿第一主函数原理”的演讲。所以就把它叫作“作用量”吧。而且，会有越来越多的人正把它称为作用量。在历史上你看到还有许多不那么有用的东西也曾被称为作用量，但我想更合理的还是改用一个新一点的定义。所以现在你也将这个新函数叫作作用量，而不久人人都会用这个简单名字去称呼它了。
现在，我要对这一课题做些讨论，它们与以前我对最少时间原理所做的讨论相似。一个宣称从一处到另一处的某个积分是一极小值的定律——这会告诉我们有关全过程的某种东西——与一个宣称当你沿路径行进时、有一个力在使它加速的定律相比，它们的特性有很大差别。第二种办法，告诉你如何沿着路径一点一点地前进；而另一种办法，是关于整个路径的全面描述。在光的情况下，我们已谈论过这两者间的关系。现在，我来解释在有了这类最小作用原理时，为什么还会有微分定律。原因是这样的：试考虑在时间和空间中的那条实际路径。如前一样，让我们仅仅考虑一维，从而可把x作为t的函数画成曲线。沿这一真实路径，S是极小值。假定已有了该真实路径，而它在空间和时间上既通过某点a，又通过附近另一点b，见图19-9。现在，如果从t1 至t2 整个积分是极小值，那么就有必要沿a至b的小段积分也是极小值。不可能在a至b这一部分就稍微多一点。因为不然的话，就总能仅仅拨动这段路径而使整个积分值稍微降低。
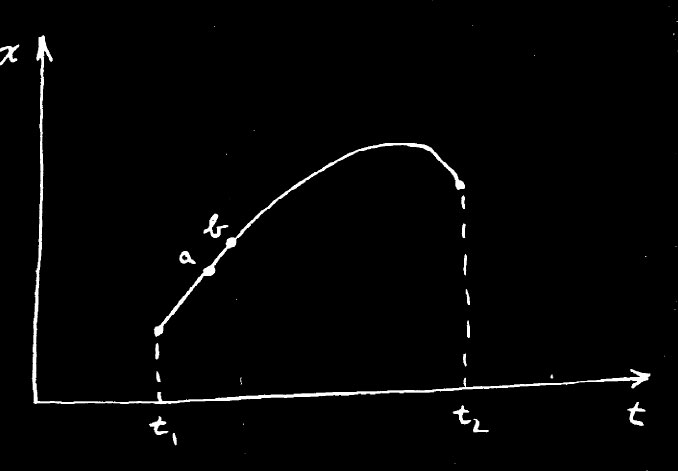
图 19-9
所以在这条路径中的每一小段也必然是极小值。并且不管该小段如何短，这都是正确的。因此，整个路径给出极小值的原理，也可说成路径的每一无限小线段也是具有最小作用量的那种曲线。现在若我们取路径上足够短的一段——在十分靠近的a与b两点之间——那么在遥远处势能如何逐点变化就是无足轻重的事情了，因为在那整整一小段路径上你几乎总是呆在同一个地点。你必须加以讨论的唯一事情就是势能中的一级变化。答案只能取决于势能的微商而不是在各处的势能。所以关于整条路径的总性质的陈述就变成对一小段路径会发生的事情的陈述——一种微分式描述。而这一种微分式描述就仅仅涉及到势能的微商，也就是在一点处的力。这就是总体定律与微分定律之间关系的一种定性解释。
在光的情况下，我们也曾讨论过这问题：粒子怎么会找到它的正确路径呢？从微分的观点，那是容易理解的。它获得加速度的每个瞬时仅仅知道在该时刻做些什么。可是如果你讲粒子决定选取将给出最小作用量的路径，那你关于因果的全部直觉就发生了混乱。为了找出邻近路径是否具有更多的作用量，它“闻出”它们了吗？在光的情况下，当我们放置一些光学元件在光所经过的道路上、以致光子们不能检查所有的路径时，我们便发现它们不再能算出该走哪一条路，从而就有了衍射现象。
这类事情在力学中也会发生吗？粒子真的不仅仅能选取正确路径，而且还会审查所有其他的各种可能路径吗？而且，若在路途上设置一些东西以阻止其向四处张望，我们也能得到与衍射类似的现象吗？当然，一切令人惊奇之处就在于，事情恰恰是这样。这正是量子力学定律所说的。因此，我们的最小作用原理还是陈述得不完全。并非粒子选取了作用最小的那条路径，而是它对附近的所有路线都闻过，从而按照与光选择最短时间类似的方法来选取一条具有最小作用量的路径。你应记得，光选取最短时间的办法是这样的：要是它遵循一条需要不同时间的路径，则当它到达时就有不同相位。而在某一点上的总振幅等于光能到达的所有不同路径振幅贡献的总和。所有那些提供相位差异很大的路径将不会合成任何东西。但如果你能找出一整序列路径，它们都具有几乎相同的相位，则小小的贡献便将加在一起而在到达之处得到一个可观的总振幅。因此，重要路径就成为许多能给出相同相位彼此靠近的路径。
对于量子力学，事情恰巧完全相同。整个量子力学（对于非相对论情况，并略去电子自旋）是这样处理的：一个粒子在时刻t1 从点1出发，将在t2 到达点2的概率等于概率幅的平方。总概率幅可以写成每一可能路径——每一条到达的途径——的各概率幅之和。对于我们可能有的每个x（t）——对于每条可能想象出来的轨道——我们就得算出一个概率幅。然后再把它们相加起来。对于每条路径，我们认为概率幅是什么呢？上述作用量积分告诉我们，对于一条单独路径其概率幅应该是什么。概率幅正比于某个常数乘eiS/ћ ，其中S就是对那条路径的作用量。这就是说，如果我们用一个复数来表示概率幅的相位，则相角就是S/ћ。作用量S具有能量乘时间的量纲，而普朗克常量ћ也具有相同的量纲。它是判定量子力学什么时候才显得重要的一个常数。
这就是它工作的原理：假设对所有路径，与ћ相比S很大，则一条路径贡献一定的概率幅。对于附近一条路径，该相位已很不相同，因为对于巨大的S，即使S的一个小小变化也意味着一个完全不同的相位——因为ћ是那么小。所以在求和时，互相靠近的路径一般都会将其效应互相抵消——除了一个区域以外，而这个区域一条路径与其邻近路径在一级近似下全都会给出相同的相位（更准确地说，在ћ范围内给出相同的作用量），只有这些路径才是重要的。因此，在普朗克常量ћ趋于零的极限情况下，正确的量子力学规律可以总结成简单的一句话：“忘记所有这些概率幅吧。粒子就在一条特殊路径上运动，那是在一级近似下S不发生变化的一条路径”。这就是最小作用原理与量子力学之间的关系。量子力学可以用这种形式来表达的事实，是由本次演讲开头曾提及的同一位教师巴德先生的另一名学生在1942年发现的［量子力学原本是通过给出关于概率幅的微分方程（薛定谔首创）以及通过某种其他矩阵数学（海森伯首创）而表达出来的］。
现在要来谈谈物理学中其他的极小原理，其中有许多是很有意义的。我并不想马上就将它们全都罗列出来，而只打算再描述其中的一种。以后，当我们面临一个具有漂亮的极小原理的物理现象时，我将随时结合它来谈。现在我要来证明：不必通过给出场的微分方程，而是通过讲述某个积分是极大或极小值，就能够描述静电学。首先，让我们考虑电荷密度处处已知的情况，而问题就在于求出空间中每一处的电势ϕ。你知道答案应该是：
▽2 ϕ=-ρ/∈0 .
但表述这相同事件的另一种办法却是：计算积分U* ：
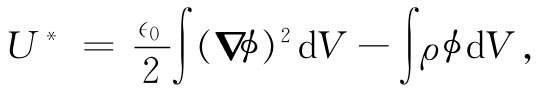
这是一个对全部空间进行的体积分。对于正确的势分布ϕ（x，y，z），U* 是极小值。
我们可以证明，这两种关于静电学的表述是等效的。现在假定选取任意函数ϕ。要求证明：当我们认为ϕ是正确的势ϕ 加上一个小的偏离f时，则在一级近似下U* 的变化为零。因此我们记作
ϕ=ϕ +f.
ϕ 就是我们所要寻找的，但现在给它造成一种变化，以找出它必须怎样才能使U* 的变分在一级近似下为零。对于U* 中的第一部分，我们有必要写成
（▽ϕ）2 =（▽ϕ ）2 +2▽ϕ ·▽f+（▽f）2 .
式中会变化的唯一一个一级项为
2▽ϕ ·▽f.
在U* 的第二项中，被积函数为
ρϕ=ρϕ +ρf，
其变化部分为ρf。因此，若只保留那些变化的部分，则需要有下面的积分：
ΔU* =∫（∈0 ▽ϕ ·▽f-ρf）dV.
现在，根据以往的普遍法则，我们必须得到经过了补缀的完全去掉f的微商的那种东西。让我们看看那些微商是什么。上式中的点积为
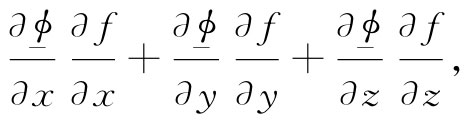
我们得把它们对x，对y和对z进行积分。原来窍门就在这里：若要将∂f/∂x去掉，就必须对x进行分部积分，这样就会把微商移到ϕ 上去。这与我们过去常用来去掉对t微商的那种一般想法是相同的。我们利用等式：
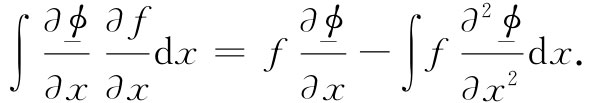
等号右边已积出的项为零，因为我们必须使f在无限远处为零［这相当于使η在t1 和t2 时为零。因此，我们的原理就应该更准确地说成：对于正确的势ϕ ，U* 比对任何其他势ϕ（x，y，z）都小，而在无限远处ϕ 和ϕ则有相同的值］。然后我们对于y和z也这样做。因而ΔU* 的积分为
ΔU* =∫（-∈0 ▽2 ϕ -ρ）fdV.
为了使这一变分对于任何f——不管是什么——都为零，f的系数就必须为零，因而
▽2 ϕ=-ρ/∈0 .
我们又回到了原来的方程。因而上述的“极小”命题是正确的。
如果我们采用稍微不同的方法来做上述代数运算，就可以使命题普遍化。让我们回到原来的式子，不计算各分量，而直接做分部积分。注意下列这个等式：
▽·（f▽ϕ ）=▽f·▽ϕ +f▽2 ϕ .
如果算出左边的微分，就能证明它刚好等于右边。现在可以利用这一等式进行分部积分。在上述ΔU* 的积分中，用▽·（f▽ϕ ）-f▽2 ϕ代替▽ϕ ·▽f，而后对体积进行积分。其中散度项的体积分可以用面积分代替：
∫▽·（f▽ϕ ）dV=∫f▽ϕ ·nda.
由于是对全部空间积分，所以积分的面位于无限远处。由于那里的f等于零，因而得到与前面相同的答案。
只有现在我们才明白怎样求解这样的一个问题，即我们不 知道其中全部电荷如何分布。假设我们有些导体，电荷以某种方式分布在其上面，只要所有导体的电势都固定不变，则我们仍然能够应用极小原理。对U* 的积分仅在一切导体之外的空间中进行。这时，由于不能使导体上的ϕ 发生变化，所以在所有导体的表面上f都等于零，因而面积分
∫f▽ϕ ·nda
仍然为零。剩下来的体积分
ΔU* =∫（-∈0 ▽2 ϕ -ρ）fdV
只在各导体之间的空间中进行。当然，我们再次得到泊松方程：
▽2 ϕ =-ρ/∈0 .
这样就证明了原来的积分U* 也是一个极小，只要在电势全都固定的各导体外的空间里进行计算［这就是说，当x，y，z是导体表面上的一点时，任何尝试函数ϕ（x，y，z）都必须等于该导体的给定电势］。
一个有趣的情况是电荷只存在于导体上。这时
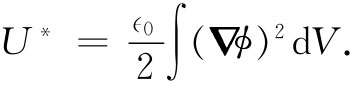
我们的极小原理讲，在一组导体都处于某些给定电势的情况下，它们之间的势就会自动调整到使积分U* 为最小。这个积分是什么呢？由于项▽ϕ就是电场，因而该积分就是静电能。真实的场是在所有来自电势梯度的场中总能量最小的那个场。
我想要利用这一结果来算出某个具体的东西，从而给你们看看这些东西实际上是非常有用的。假设我取两个导体构成一柱形电容器（图19-10），内部的导体具有电势V，而外面的导体电势为零。令内、外两个导体的半径分别为a和b。现在可以假定它们之间的任意
电势分布。如果我们采用正确
的ϕ
并算出∈0
/2∫（▽ϕ
）2
dV，则它应当是系统的能量，即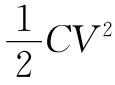
。因此，也可以根据我们的原理算出C。但若采用错误的势分布并试图用这个办法来算出C，则我们得到的电容将太大。因为电势V已经被规定了，所以任何假定出来的、并非严格等于正确电势的ϕ，都会给出一个比正确值要大的假的C。不过如果我的辅助的ϕ是任意的粗略近似，则C将是一个良好的近似，因为C的误差比ϕ的误差要高一级。
图 19-10
假设我不知道一个柱形电容器的电容，那我就可以利用这一原理来找到它。我只要不断对势函数ϕ进行猜测直到获得最低的C值为止。例如，假定我选取一个与恒定电场相对应的势（当然，你知道，这里的场实际上不是恒定的，它会随1/r变化）。一个恒定场意味着一个与距离成正比的势。为适合两导体所在处的条件，它必须是
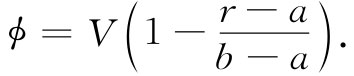
这个函数在r=a处为V，在r=b处为零，而在两者之间的势则有等于-V/（b-a）的固定斜率。所以为了求得积分U* ，我们所要做的就是将这个ϕ的梯度的平方乘以∈0 /2并对全部体积求积分。让我们对单位长度的圆柱做这种计算。在半径r处的体积元为2πrdr，进行积分，我对求电容的第一次尝试就得到
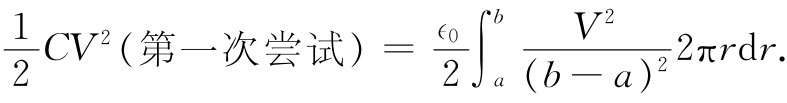
这积分不难，它正好为
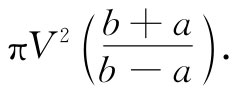
这样我就有了一个关于电容的公式，它虽然不正确，但却是一种近似结果：
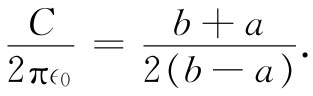
自然，它与正确答案C=2π∈0 /ln（b/a）不同，但并非太坏。让我们对几个b/a值把它与正确答案做比较，所得结果如下表所列：
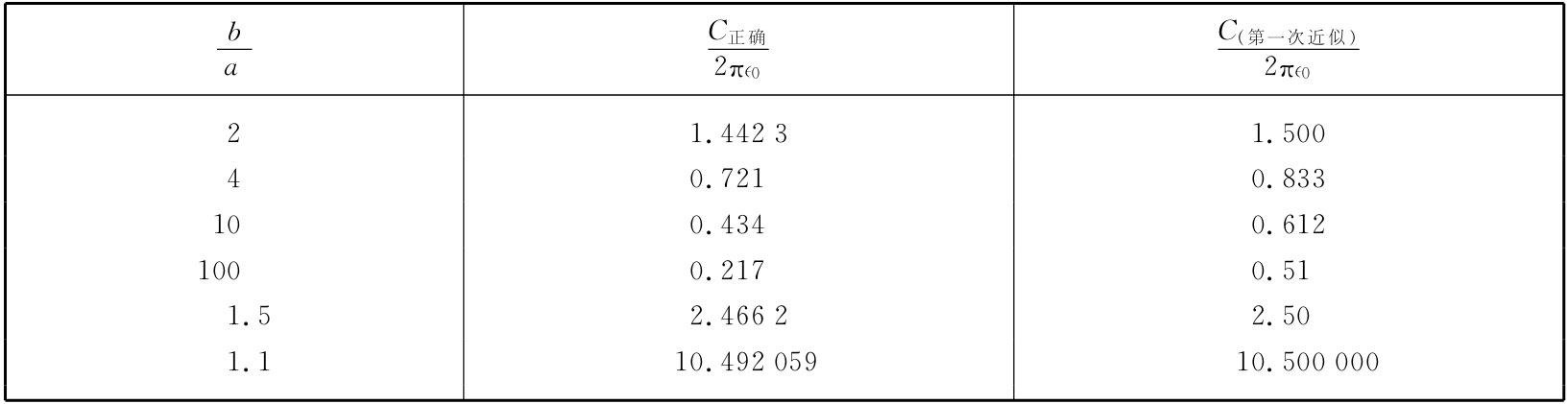
即使当b/a大至2时——就电场来讲，与一个线性变化的场相比它给出了相当大的改变——我仍获得了相当好的近似。当然，正如所预期的那样，答案稍微偏高一些。如果你把一根细导线放在一个大圆柱之中，事情就糟得多。这时场已有了巨大变化，而倘若你还是用一个恒定场来代表它，那你就干得不太好了。当b/a=100时，我们偏离了几乎2倍。对于小的b/a，则事情要好得多。试取与刚才极端相反的情况，当两导体相距不远——比方说b/a=1.1——时，则恒定场就是一个相当好的近似，而我们会得到误差在千分之一以内的正确C值。
现在我要来告诉你，如何可改进这种计算（当然，对于柱形电容器来说你已经知道 它的正确答案，但对于其他一些你还不知道其正确答案的古怪形状，所用方法仍然与此相同）。下一步对未知的正确ϕ尝试较好的近似。例如，你也许会试一试一个常数加上一个指数函数的ϕ，如此等等。但除非你已知道正确的ϕ，否则你怎么会知道何时才能得到一个较好的近似呢？答案：你把C算出来，最低的C值就是最接近于正确的值。让我们来尝试这一想法。假定电势不是r的线性函数而是r的二次函数——电场不是恒定的而是线性的。能够适合在r=b处ϕ=0、而在r=a处ϕ=V这种条件的最一般的二次形式的ϕ为
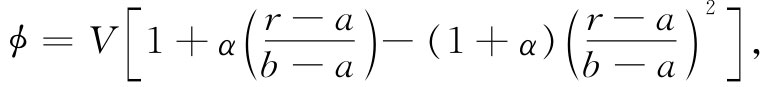
式中α为一任意常数。这公式稍微复杂了一点。在势中除了一个线性项外还包括一个二次项。很容易从它得到场，该场正好为
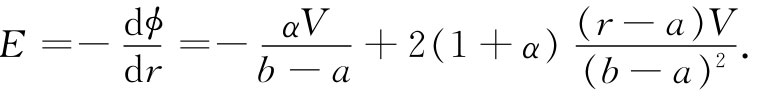
现在我们必须将上式加以平方并对体积进行积分。但请等一等。我应当给α取个什么值呢？我可以对ϕ取一条抛物线，然而是什么样的抛物线呢？这里我所要做的是：用任意一个 α算出电容。得到的结果是
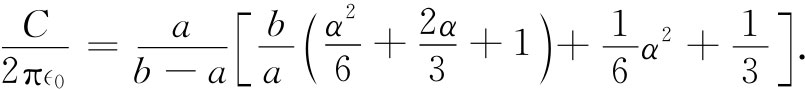
这看来还是稍微复杂一点，但它是从对场的平方进行积分而得到的。现在我可以选择α了。我知道正确结果总是比我将要算出的任何值都小，因而不管我代入什么α值总会得到一个太大的答案。但如果我保持着玩弄α并得到一个我所能得到的最低的可能值，则这个最低值就会比其他任何值都更接近于真实的值。所以我将要做的下一件事就是去拣出会提供极小C值的那个α。按照普通的微积分来计算，我得到极小的C出现在α=-2b/（b+a）时，将此值代入上面的公式中，得到的极小电容为：
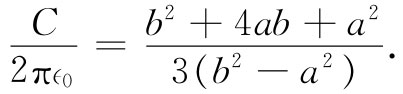
对于各种不同的b/a值我已经算出了由这一公式所给出的C值。我将称这些数值为C（二次），这里是C（二次）与正确C的对照表。
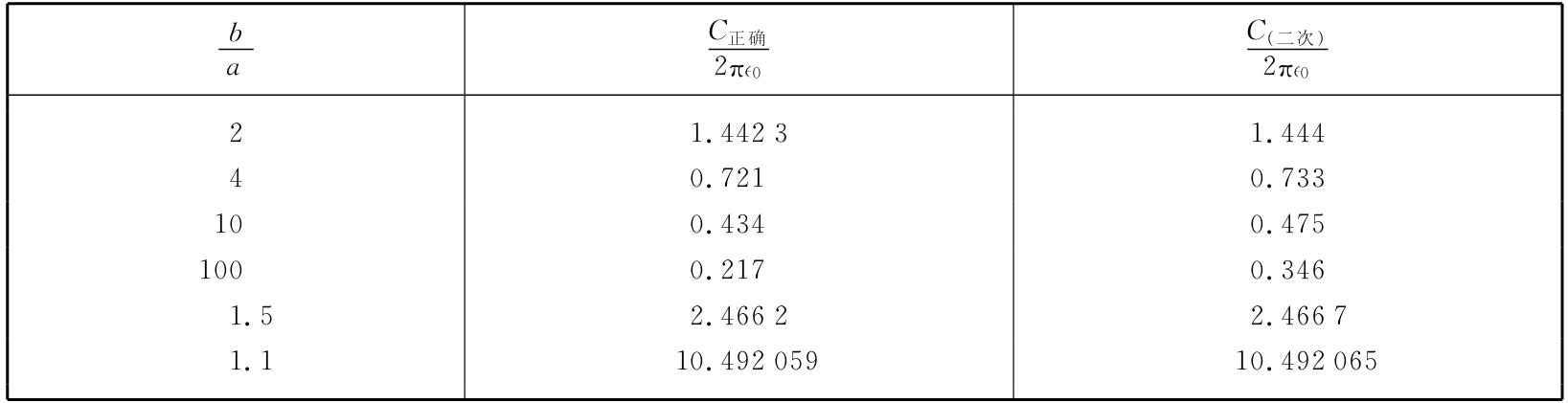
例如，当两半径之比为2比1时，我得到1.444，这对于正确答案1.4423来说已经是一个很好的近似。即使对于较大的b/a，它仍旧相当好——比一次近似要好得多。当b/a为10比1时，还是相当准确——只偏离10%。但当b/a达到100比1时，事情就开始变糟。我所得到的C/2π∈0 是0.346而不是0.217。在另一方面，对于1.5的半径比，该答案非常好；至于1.1的b/a，答案表明是10.492065而不是10.492059。这里答案应该是好的，它就已经非常非常好了。
我已经举出了好几个例子，首先为了表明极小作用量原理和一般的极小原理的理论价值，其次在于表明它们的实用价值——不仅仅去算出我们已明知其答案的电容。对于任何其他形状的电容，你可以用某些像α那样的未知参数去猜测一个近似的场，并调整这些参数以获得一个极小值。对于其他方法难以处理的一些问题，用此法你将得极好的数值结果。