图31-1 在一块各向异性的晶体中,极化强度的矢量加法
物理学家总有这么一种习惯,即取任何现象的最简单例子并称之为“物理学”,而把那些更复杂的例子留给其他学科——诸如应用数学、电工学、化学、晶体学等——去处理。甚至固体物理几乎只算得半个物理学,因为它对一些特殊物质操心得太多。所以在这些讲演中我们将常常漏掉许多有趣的东西。例如,晶体——或大多数物质——的重要性质之一就是它的电极化率在不同方向上并不相同。如果你在任一方向加上电场,则原子的电荷将会移动一点点而产生出一个电偶极矩,可是这偶极矩的大小在很大程度上却取决于场的方向。当然,这是相当复杂的。但在物理学中我们一般通过谈论极化率在一切方向都相同的特殊情况开始,目的在于使生活过得容易些。其他情况则都留给别的部门。因此,在这一章中将要论及的东西,对于我们今后的工作来说是完全不需要的。
张量数学对于描述随方向而变的那些物质性质特别有用——尽管这只是其用途的一个方面。由于你们中大多数人不准备成为物理学家,但将会进入各种事态都与方向密切相关的现实 世界中,所以你们迟早需要用到张量。为了不遗漏任何东西,我们即将描述张量,即使不是十分详尽也罢。你们要有物理学处理问题是完整的那种感觉。例如,我们的电动力学是完整的——正如同任何电磁学课程甚至研究院课程那么完整。我们的力学不够完整,因为当过去学习力学时,你们还不具备高水平的数学技巧,因而不能讨论像最小作用原理、拉格朗日函数、哈密顿函数等那类课题,这些都是描述力学的更精致的方法 。然而,除了广义相对论之外,我们的确已有了一整套力学定律 。我们的电磁学是完整的,而一大堆其他东西也很完整。自然,量子力学还谈不上——我们得留一些东西在后头。可是,你至少应该知道张量是什么。
我们曾在第30章中强调过,结晶物质的特性在不同方向上是不同的——我们说它们是各向异性 的。感生偶极矩随所加电场的方向而改变的情况,只是我们将作为张量应用的一个例子。我们讲,对于某个给定方向的电场,单位体积内的感生偶极矩P与这外加电场E的强度成正比(如果E不太大,这对于许多物质来说都是个很好的近似)。我们将称这个比例常数为α [1] 。现在要来考虑α与外加场方向有关的那类物质,诸如像方解石那样的晶体,当你通过它看物体时会看到双像。

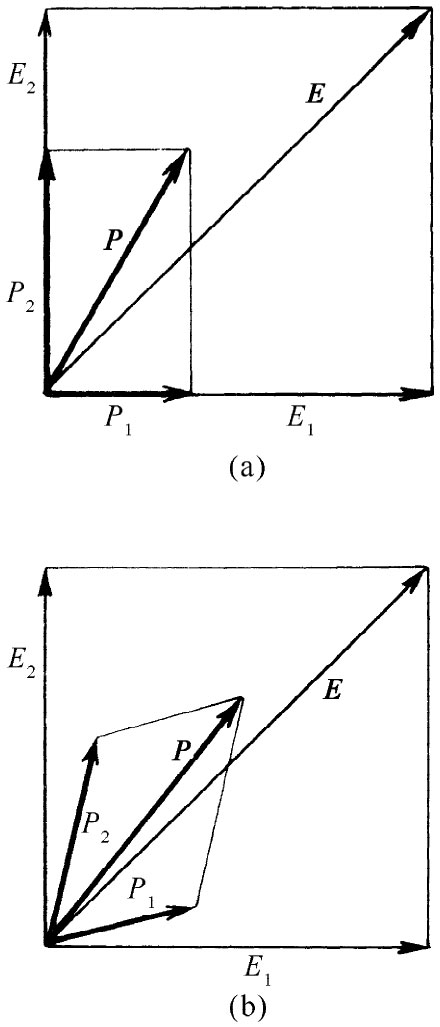
图31-1 在一块各向异性的晶体中,极化强度的矢量加法
假定在某一特定晶体中,我们已发现在x方向的电场E1 在x方向产生一个极化强度P1 。然后又发现在y方向有一个与E1 同等强度 的电场E2 ,却在y方向产生一个不同的极化强度P2 。如果我们把电场置于45°角上又将如何呢?噢,那是沿x与沿y两种场的叠加,因而极化强度P便将是P1 与P2 的矢量和,如图31-1(a)所示。极化强度不再与电场同方向了。你可以看出这结果如何才会出现。可能有些电荷很容易上下移动,但对于侧向运动则相当困难。当力作用于45°角时,电荷就会向上动得比向侧面远一些。位移并不沿外力方向,因为存在非对称的内部弹性力。
当然,对于45°并没有什么独特意义。晶体的感生极化强度不 在电场的方向上是普遍 正确的。在上述例子中,我们碰巧对于x和y轴做了一个侥幸选择,即对该两轴来说P都沿着E。要是晶体相对于坐标轴有了转动,则在y方向上的E2 就可能产生一个含有x分量也含有y分量的极化强度P。同理,起因于x方向电场的极化强度也会有x和y两个分量。那么极化强度就该如图31-1(b)所示,而不再像(a)那种模样了。事情变得较为复杂——但对于任何场E来说,P的大小 仍然正比于E的大小。
我们现在要处理晶体相对于坐标系有任意取向的那种普遍情况。沿x方向的电场将产生一个具有x,y和z各分量的极化强度P,我们可以写为
Px =αxx Ex ,Py =αyx Ex ,Pz =αzx Ex . (31.1)
这里我们正在讲述的一切就是:若电场处在x方向,则极化强度不一定在同一方向,而是含有x,y和z各分量——每个分量都正比于Ex 。我们分别称这些比例常数为αxx ,αyx 和αzx (第一个字母告诉我们P包含的分量,末一个字母则表明电场的方向)。
同理,对于一个沿y方向的场,我们可以写成
Px =αxy Ey ,Py =αyy Ey ,Pz =αzy Ey ; (31.2)
而对于一个沿z方向的场,则有
Px =αxz Ez ,Py =αyz Ez ,Pz =αzz Ez . (31.3)
原来我们已经说过,极化强度线性地依赖于场,因而若有一个兼有x和y分量的电场E,则最后得到的P的x分量将等于式(31.1)和(31.2)的两个Px 之和。如果E具有沿x,y和z的各分量,则最后得到的P的分量将等于式(31.1)、(31.2)和(31.3)的三个贡献之和。换句话说,P将由下列诸式给出:
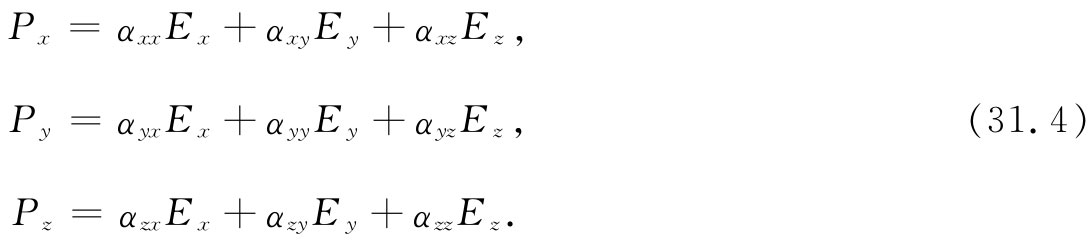
于是晶体的介电行为就由这九个量(αxx ,αxy ,αxz ,αyz ,…)完整地描述,我们可用αij 这个符号来作代表(每个下脚标i和j各代表三个可能字母x,y和z中的任一个)。一个任意电场E可以分解为分量Ex ,Ey 和Ez ,从这些我们就能够用αij 来求出Px ,Py 和Pz ,它们一起给出总极化强度P。由这九个系数αij 构成的一组数称为张量 ——在本例中,即指极化张量 。正如我们所说三个数(Ex ,Ey ,Ez )会“构成矢量E”那样,我们也可讲这九个数(αxx ,αxy ,…)“构成张量αij ”。