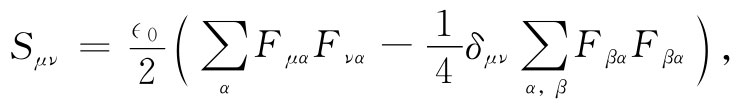
在这一章中,迄今所考察过的所有张量都是与三维空间有关的,它们被定义为在空间转动下具有某种变换性质。在第26章中,我们曾有机会用到在四维相对论性时空中的一个张量——电磁张量Fμv 。这样一个四维张量的各分量在洛伦兹坐标变换下以我们算出的特殊方式变换着(尽管我们并未那样做,但我们可能已经把洛伦兹变换认为是在叫作闵可夫斯基空间的“四维空间”里的一种转动,那么与我们这里正在做的做个类比,就会更加清楚了。)
作为最后一个例子,我们想要考虑在相对论四维(t,x,y,z)中的另一个张量。当我们在上面写出应力张量时,我们曾把Sij 定义为穿过单位面积的力的分量。可是力等于动量的变化率,因此,不说“Sxy 是穿过垂直于y方向的单位面积力的x分量”,而同样可以说“Sxy 是穿过垂直于y方向的单位面积动量的x分量的变化率”。换句话说,Sij 的每一项也各代表通过垂直于j方向单位面积的动量的i分量流。这些是纯空间分量,但它们却是在四维(μ和v=t,x,y,z)中含有像Stx ,Syt ,Stt 等附加分量的一个“较大”张量Sμv 的一些部分,我们现在就试图找出这些附加分量的物理意义。
我们知道,那些空间分量代表动量流。我们可以从研究另一种“流”——电荷流——来获得如何把它推广到时间那一维上去的线索。对于标量 电荷来说,其变化率(通过垂直于流的单位面积)就是一空间矢量 ——电流密度j。我们已经看到,这个流矢量的时间分量就是那些流动物质的密度。例如,j可以同一个时间分量jt =ρ——即电荷密度——相结合而构成一个四维矢量jμ =(ρ,j),也就是说,当jμ 中的μ取t,x,y,z各值时,它指的是标量电荷的“密度,及标量电荷在x方向的流动速率,在y方向的流动速率,在z方向的流动速率”。
现在,与刚才所做的关于一个标量流的时间分量的说法相类似,我们也许会期待,与描述动量x分量流的Sxx ,Sxy ,Sxz 一起,就应该有一个时间分量Sxt ,它应代表正在流动的那种东西的密度,也就是说,Sxt 应该是x方向动量的密度。所以我们就能够沿水平方向把我们的张量推广到包含一个t分量。我们得
Sxt =x动量密度,
Sxx =x动量的x向流,
Sxy =x动量的y向流,
Sxz =x动量的z向流.
同理,对于动量的y分量我们有三个流动分量——Syx ,Syy ,Syz ——此外还应加入一个第四项:
Syt =y动量密度.
而当然,在Szx ,Szy ,Szz 之外我们也应该加上
Szt =z动量密度.
在四维中还有一个动量的t分量,我们知道那就是能量。因此,张量Sij 应该在垂直方向上 [3] 用Stx ,Sty 和Stz 来推广,其中
Stx =能量的x向流,
Sty =能量的y向流,
Stz =能量的z向流. (31.28)
这就是说,Stx 是单位时间内穿过垂直于x轴单位面积的能流,等等。最后,为使张量达到完整,还需要Stt ,那该是能量密度 。我们已把三维的应力张量Sij 推广成四维的应力-能量张量 Sμv 。那下脚标μ可以取四个值t,x,y和z,它们分别指“密度”、“在x向单位面积的流动”、“在y向单位面积的流动”、“在z向单位面积的流动”。同样地,v取t,x,y,z四个值就告诉我们什么 在流动,即“能量”、“沿x向的动量”、“沿y向的动量”和“沿z向的动量”。
作为一个例子,我们将讨论不是在实物中,而是在一个存在着电磁场的自由空间区域里的一个张量。我们知道,能流就是坡印亭矢量S=∈0 c2 E×B。因此,S的x,y和z分量,从相对论的观点来看,就是我们的四维应力能量张量的分量Stx ,Sty 和Stz 。张量Sij 的对称性也同样移到了t分量,因而四维张量Sμv 是对称的:
Sμv =Svμ . (31.29)
换句话说,代表x,y和z动量密度 的Sxt ,Syt ,Szt 也等于坡印亭矢量S,即能流 的x,y和z分量——正如我们在前面一章中曾用不同的论证所证明过的那样。
这电磁应力张量Sμv 的其余各分量也可用电磁场E和B来表示。这就是说,必须把应力——或较少神秘性地说成是动量流——纳入电磁场之中。在第27章中与式(27.21)有关的地方我们曾对此有所讨论,但还未将其细节算出。
那些想要在四维张量方面锻炼本领的人们,也许乐于见到用场来表示的关于Sμv 的公式:
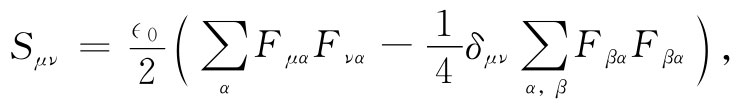
其中对于α,β的求和是指对于t,x,y,z的求和,不过(如同在相对论中经常做的那样)我们采用关于求和符号∑与符号δ的特别含义。在总和中有关x,y,z的项都要去掉 ,并且δtt =1,δxx =δyy =δzz =-1,对于μ≠v则δμv =0。你能否证实(令c=1)它会给出能量密度Stt =(∈0 /2)(E2 +B2 )和坡印亭矢量∈0 E×B?你能否证明:在B=0的静电场中,应力的主轴在电场的方向,而且有一个张应力 (∈0 /2)E2 沿电场方向,还有一个相等的压强 垂直于电场方向?
[1] 在第10章中,我们曾按照通常惯例并写出P=∈0 χE,而称χ(“khi”)为“电极化率”。这里采用一个单独字母将更方便,所以就把∈0 χ写成α。对于各向同性的电介质来说,α=(κ-1)∈0 ,其中κ为介电常量(见§10-4)。
[2] 由电场产生 极化而做的功,不应与永偶极矩p0 的势能-p0 ·E互相混淆。
[3] 这表明是一个与x,y,z各轴都“正交”的方向,即t方向。——译者注