
现在想要取得有关张量的某些经验。假定我们提出一个有趣问题:要使晶体极化需要多少能量(除了我们已知的电场中单位体积能量∈0 E2 /2以外)?暂时考虑那些正在发生位移的原子电荷。使电荷移动距离dx所做的功为qEx dx,而倘若单位体积中有N个电荷,则所做总功为qEx Ndx。但qNdx又是单位体积中的偶极矩变化dPx ,因而单位体积 所需的能量就是
Ex dPx .
把场的三个分量所做的功合起来,就可得到单位体积的功为
E·dP.
由于P的大小正比于E,因此在使P从0增大至P时对单位体积所做的功就是对E·dP的积分。把这个功叫作uP [2] ,就可写出

现在可以根据式(31.5)用E表示P,因而有

这能量密度uP 是一个与坐标轴的选择无关的数值,因此是一个标量。这样,张量便有这么一种性质,即当它对其中一个下脚标(即对一矢量)求和时,会给出一个新的矢量;而当它对两个 下脚标(即对两个 矢量)都求和时,则会给出一个标量。
张量αij 实际上应称为“二阶张量”,因为它有两个下脚标。矢量——带有一个 下脚标——是一阶张量,而标量——完全没有下脚标——则是零阶张量。因此我们讲,电场E是一阶张量,而uP 则是零阶张量。有可能把张量的概念推广到三个或四个下脚标,因而形成了高于二阶的张量。
极化张量的下脚标取遍三个可能的数字,这是三维中的张量。数学家会考虑在四维、五维或更多维中的张量。我们在对电磁场的相对论性描述中已采用过一个四维张量Fμv (第26章)。
极化张量αij 具有一个有趣的性质,即它是对称 的,这就是说,αxy =αyx ,而对于任何对下脚标都是如此(这是实际晶体的一种物理 性质,而对一切张量并不一定如此)。你可以通过在下述循环中计算晶体的能量变化而自己去证明那必然是正确的:(1)在x方向加一电场;(2)在y方向加一电场;(3)除去 沿x方向的场;(4)除去沿y方向的场。现在晶体已回到原来出发时的那个状态,因而在极化过程中所做的净功必须回到零。然而,你能够证明,要此事成立,αxy 必须等于αyx 。当然,相同种类的论证也可对αxz 等等进行。因而极化张量是对称的。
这也就意味着,极化张量可以通过只测量在不同方向上使晶体极化所需的能量而加以测定。假设我们加上一个只有x和y分量的E场,那么按照式(31.7),就有
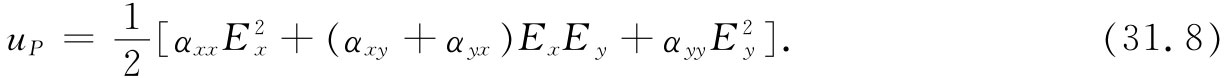
仅用一个Ex 场,就可以测定αxx ;仅用一个Ey 场,则可以测定αyy ;若同时用Ex 和Ey 两者,还可得到由含有(αxy +αyx )这一项而引起的附加能量。由于αxy 与αyx 相等,所以这一项为2αxy ,并且可以与能量联系起来。
式(31.8)的能量表示式具有漂亮的几何解释。假设我们问起对应于某一给定 能量密度——比如说u0 ——该有什么样的场Ex 和Ey ,那恰好就是求解下列方程式的数学问题:
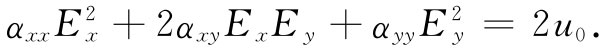
这是一个二次方程,因此如果我们把Ex 和Ey 画成曲线,则这一方程的解便是在一个椭圆上的所有各点(图31-2)(它必须是个椭圆,而不是一条抛物线或双曲线,因为任何场的能量总是正的而且是有限的)。具有分量Ex 和Ey 的矢量E可以从椭圆的原点画到椭圆上,因此,像这样的一个“能量椭圆”就是使极化张量“形象化”的一种巧妙方法。
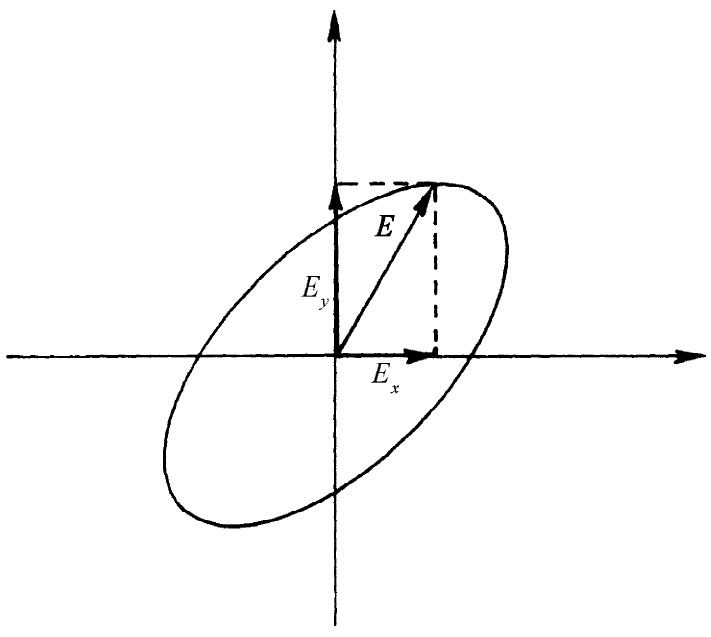
图31-2 提供恒定极化能的矢量E=(Ex ,Ey )的轨迹
如果我们现在推广至包括所有三个分量的情况,则所需在任何 方向提供单位能量密度的电场矢量E就会在椭球表面上给出一点,如图31-3所示。这个恒定能量椭球的形状唯一地表示着张量极化率的特征。
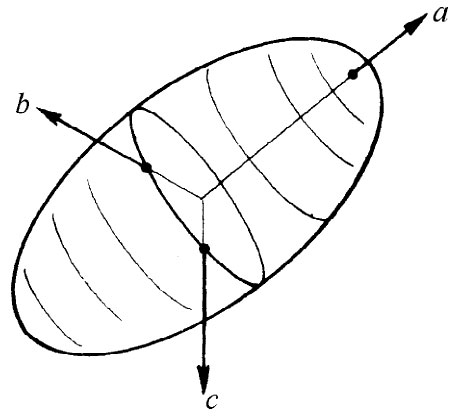
图31-3 极化张量的能量椭球
原来椭球具有这么一个有趣性质,即它总是可以简单地通过给出三个“主轴”方向以及沿这些轴的椭圆直径而加以描述。“主轴”的方向就是最长直径与最短直径的方向以及与两者都正交的另一方向。它们由图31-3中a,b和c三根轴所标明。相对于这些轴,椭球具有特别简单的方程
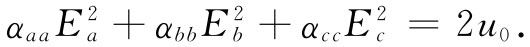
因此,相对于这些轴,介电张量就只有三个不等于零的分量:αaa ,αbb 和αcc 。这就是说,不管晶体如何复杂,总能够选取一组坐标轴(不一定是晶体本身的轴),在其中极化张量只有三个分量。用这样一组坐标轴,式(31.4)便简单地变成
Pa =αaa Ea ,Pb =αbb Eb ,Pc =αcc Ec . (31.9)
沿任何一个主轴的电场将产生沿同一个轴的极化,当然这三条轴的系数可能是不同的。
人们往往这样来描述张量,即把那九个系数列在一个方括号内:

对于主轴a,b和c来说,只有那些对角线的项才不等于零,这时我们就说“张量是对角的”。整个张量为

重要之处在于,任何极化张量(实际上,在任何维数中凡属于二阶的任何对称 张量)都可以通过选取适当的一组坐标轴而写成这种形式。
若对角形极化张量的三个元素都相同,即如果
αaa =αbb =αcc =α, (31.12)
则能量椭球就变成圆球,极化率在所有方向都相同,这种材料就是各向同性的。在张量符号表示法中,
αij =αδij , (31.13)
式中δij 为单位张量

当然,这意思是:
δij =1, 若i=j;
δij =0, 若i≠j; (31.15)
这个δij 张量通常称为“克罗内克δ”。你可以这样来自己取乐,即证明:若把坐标系改变成任何其他的直角坐标系,则张量式(31.14)仍然具有完全相同形式。式(31.13)的极化张量会给出
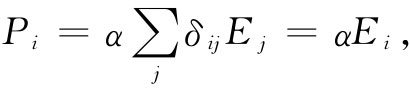
这个式子意味着与我们以前关于各向同性电介质的结果
P=αE
相同。
极化椭球的形状和取向有时可与晶体的对称特性联系起来。我们曾在第30章中说过,三维晶格共有230种不同的可能内部对称性,而对于许多目的来说,它们可以按照单胞的形状方便地归纳成七类。现在这极化椭球就应该分享晶体的这些内禀几何对称性。例如,三斜晶体具有低级对称——其极化椭球将有互不等长的轴,而每一轴的方向一般都没有与晶轴排成一线。另一方面,单斜晶体具有这样的特性,即如果晶体对其中的一轴转过180°,它的性质不会改变。所以在经过了这样一个转动之后极化张量应仍然相同。结果是,极化椭球在经过了180°转动后就必须回到其本身,这只有在该椭球的一根轴与晶体的对称轴的方向相同时才能发生。除此之外,这个椭球的取向和大小都不受限制。
可是对于正交晶体,该椭球的诸轴就必须都对应于各晶轴,因为围绕三个轴中任一轴的180°转动都将重复同一晶格。如果我们涉及四方晶体,则椭球必须具有相同的对称性,因而就必然会有两根相等的直径。最后,对于立方晶体来说,椭球的所有三根直径都必须等长,它变成了一个球,而晶体的极化率在所有方向就都相同。
对晶体的一切可能对称性算出各种可能有的张量类型将是一场大型游戏,这称为“群论”分析法。但对于极化张量的简单情况,要看出其中关系应该会怎么样,还是相对容易的。