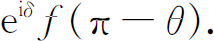
在上一章里，我们开始考虑发生在两个全同粒子 相互作用的过程中振幅干涉的特殊法则。所谓全同粒子 是指像电子那样的无法将它们彼此区别开来的粒子。如果在某一个过程中包含两个全同的粒子，将到达计数器的粒子与另一粒子互相调换一下，这样调换后的状态与原来的状态是不能区别的，而且——像所有其他不能区别的情况一样——调换后的状态与原来的状态相干涉。于是事件的振幅就是两个相干振幅之和，但是，令人感到有趣的是，在某些情况下两个振幅以相同的 相位相干涉，而在另一些情况下，振幅以相反的 相位相干涉。
假设两个粒子a 和b 相互碰撞，其中a 散射到方向1而b 散射到方向2，如图4-1（a）所示。令f （θ ）为这一过程的振幅，于是，观察到这个事件的概率P 1 正比于|f （θ ）|2 。当然也可能发生另一种过程，即粒子b 散射到计数器1中而粒子a 进入计数器2中，如图4-1（b）所示。假设不存在由自旋之类所定义的特殊方向，这一过程的概率就是|f （π－θ ）|2 ，因为这正好等于在第一过程中把计数器1移到π－θ 角处。你们也许会想到，第二个过程的振幅正巧等于f （π－θ ）。但它并不一定是这样，因为还可以有一个任意的相位因子。这就是说振幅可以是
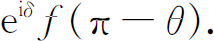
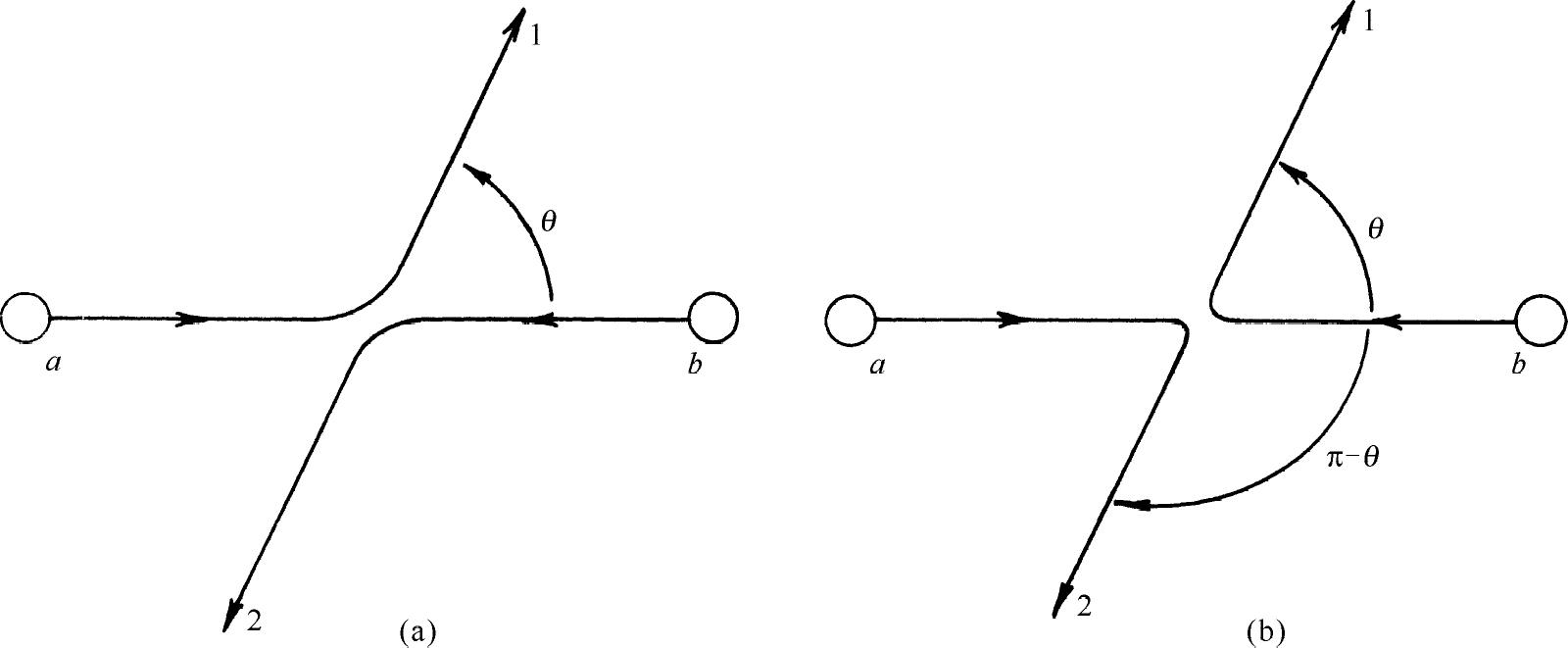
图4-1 在两个全同粒子的散射过程中，（a）和（b）两个过程不能区别
这个振幅仍旧给出概率P 2 等于|f （π－θ ）|2 。
现在让我们来看一看，如果a
和b
是全同粒子的话，将会出现些什么情况。这时我们就不能区别图4-1中的两个图所表示的不同过程。对于无论
a
还是b
进入计数器1而同时另一个进入计数器2的情形，有一个振幅。这个过程的振幅是图4-1所示的两个过程的振幅之和。假使我们把第一个过程的振幅叫做f
（θ
），那么第二个就是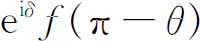
。现在，相位因子就很重要了，因为我们要把两个振幅相加。假设当我们把这两个粒子的角色交换时，我们必须在振幅上乘以某个相位因子，如果我们把这两个粒子再交换一次，我们应该再次乘以同样的因子。可是这样一来，我们又回到了第一过程。相位因子应用两次必然回到原来的状态——相位因子的平方必定等于1。这只存在着两种可能性：eiδ
等于＋1或者等于－1。两个粒子交换前后的振幅要么是有相同的符号，要么具有相反的符号。这两种情况在自然界中都存在，它们分别对应于不同种类的粒子。以正号
相干涉的粒子称为玻色子
，以负
号相干涉的粒子称为费米子。光子、介子和引力子都是玻色子，电子、μ
子、中微子、核子和重子都是费米子
。于是，我们得到全同粒子的散射振幅是：
玻色子 ：
费米子 ：
对于具有自旋的粒子——如电子——还有一个另外的复杂情况．我们不仅要详细说明粒子的位置，还要说明它们自旋的方向。只对于是有相同自旋状态 的全同粒子相互交换时振幅才相互干涉。如果考虑非极化射束——这是不同自旋状态的混合物——的散射，还有某些特别的计算。
当两个或更多的粒子紧紧地束缚在一起的时候，将出现一个有趣的问题。例如，一个α 粒子里面有4个粒子——两个中子和两个质子。当两个α 粒子相互散射时，有几种可能性。在散射过程中，可能有一个中子从一个α 粒子跳到另一个α 粒子中的一定振幅，同时在另一个α 粒子中有一个中子跳过来和它交换位置，于是散射以后的α 粒子已经不是原来的粒子了——已经交换了一对中子。见图4-2。交换一对中子的散射振幅和没有这种交换的散射振幅相干涉，由于这里有一对费米子相互交换，干涉必定具有负号。另一方面，如果两个α 粒子的相对能量是如此之低，使得它们保持相当的距离——譬如说由于库仑斥力——那么就不可能有交换任何内部粒子的概率。于是我们可以把α 粒子当作结构单一的客体而不必去考虑它的内部细节。在这种情形下，只有两种情况对散射振幅有所贡献，在散射过程中要么没有粒子交换，要么4个粒子都交换。因为α 粒子中的质子和中子都是费米子，任意一对粒子的交换都要改变散射振幅的符号。只要在α 粒子之间没有内部粒子的交换，交换两个α 粒子和交换4对费米子是同样的。对于每一对费米子的交换都要改变符号，其结果是振幅以正号相组合。α 粒子的行为像玻色子。
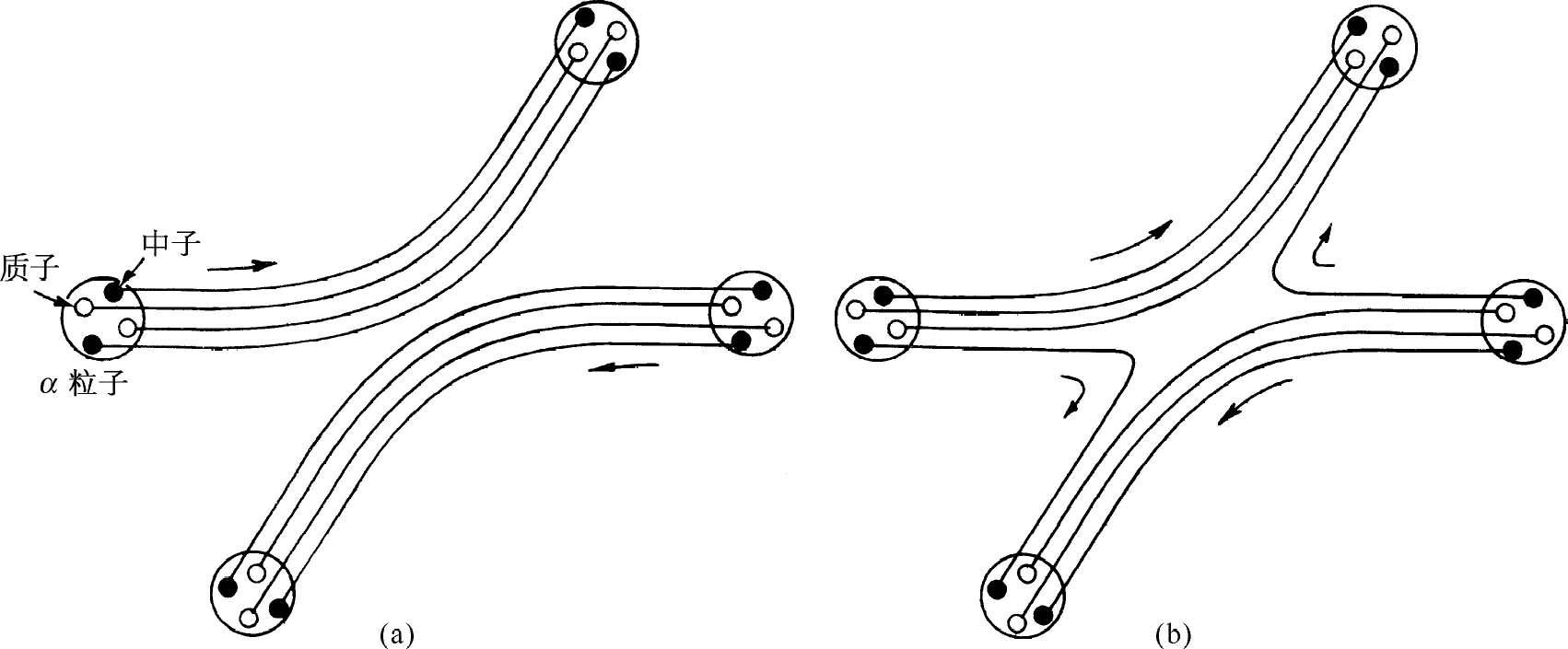
图4-2 两个α 粒子的散射。在（a）中，两个α 粒子保持原来的样子不变；在（b）中，碰撞时互相交换一个中子
因此，关于复合粒子的法则是这样的，在复合粒子可以看成单个粒子的情况下，复合粒子的行为像费米子还是像玻色子取决于它们包含的是奇数个费米子还是偶数个费米子。
所有我们提到过的基本费米子——例如电子、质子以及中子等等——具有自旋j ＝1/2。如果将几个这样的费米子放在一起组成一个复合粒子，总的自旋不是整数就是半整数。例如，氦的普通同位素He4 ，它的原子核包含两个中子和两个质子，其自旋为零。而Li7 的原子核有3个质子和4个中子，具有3/2的自旋。我们以后要学习角动量的合成规则，而现在只提一下，每一个具有半整数自旋 的复合粒子就像一个费米子 ，而每一个具有整数自旋 的复合粒子就像一个玻色子 。
这就提出了一个有趣的问题：为什么具有半整数自旋的粒子是费米子，它们的振幅要以负号相加；而具有整数自旋的粒子是玻色子，它们的振幅以正号相加？很抱歉，对于这个问题我们不能给出一个简单的解释，泡利曾从量子场论和相对论的复杂的论证中作出过一个解释，他指出，量子场论和相对论必须一起应用。但是我们无法在初等的水平上找到一种方法来重复他的论证。看来这是物理学中不多的情形之一，在这些情形中具有能非常简明表述的法则，但是没有人能为它找到简单而又容易的解释。这种解释要深入到相对论量子力学中。这可能意味着我们还没有完全理解其中所包含的基本原理。目前，你们只好把它当作自然界的一个法则接受下来。
现在我们来讨论关于玻色子相加法则的一个有趣的结果。这和有几个粒子出现时的行为有关。我们先考虑两个玻色子从另外两个粒子上散射的情形。我们不去关心散射机构的细节，我们只对被散射粒子发生些什么变化感兴趣。假设情况如图4-3所示。粒子a 被散射到状态1。所谓状态 系指一定的运动方向和能量，或者别的某种给定的条件。粒子b 被散射到状态2。我们假设这两个状态1和2几乎相同。（事实上我们所要求的是两个粒子被散射到相同的方向或状态的振幅；但是最好我们先考虑一下如果两个状态几乎相同时会发生些什么，然后再解决当两个状态变为完全相同时，会发生些什么。）
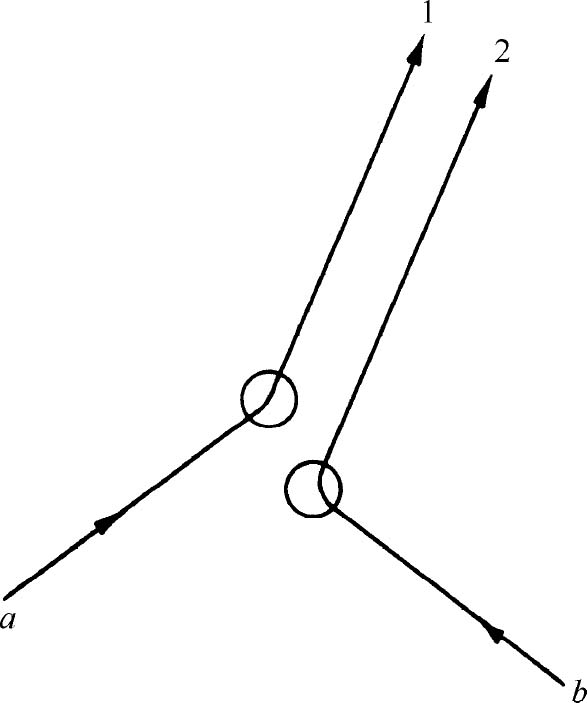
图4-3 一对粒子被散射到靠近的终态
假定我们只有粒子a ，它具有一定的振幅被散射到方向1，写成〈1|a 〉。而粒子b 单独存在时，它被散射到方向2具有振幅〈2|b 〉。如果两个粒子不相同，两次散射同时发生的振幅就是乘积
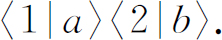
于是发生这一事件的概率为
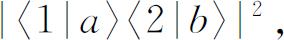
它也等于
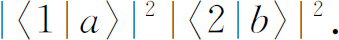
在目前的论证中，为了使书写方便，有时我们令
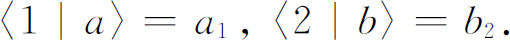
于是，双散射的概率是
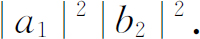
也可能发生这样的情况：粒子b 散射到方向1，而粒子a 散射到方向2。这一过程的振幅是
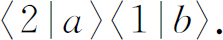
这个事件的概率是
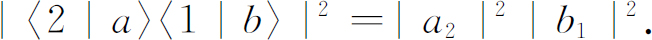
现在，设想我们有一对小型计数器，可以用它们来检测这两个被散射的粒子。它们同时检测到两个粒子的概率P 2 为
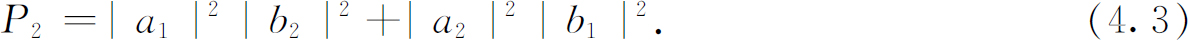
现在让我们假设方向1和2非常靠近，我们期望a 应随着方向连续地变化，所以当1和2互相靠近时，a 1 和a 2 也必定彼此趋近。当方向1和2足够接近时，振幅a 1 和a 2 将相等。我们可以令a 1 ＝a 2 ，并把它们都称为a ，同样令b 1 ＝b 2 ＝b 。于是我们得到
现在假设a 和b 是全同的玻色子。那么，a 进入1而b 进入2的过程和相互交换后a 进入2而b 进入1的过程不能区别。假使这样，这两个不同过程的振幅 相互干涉。两个计数器各俘获一个粒子的总 振幅是
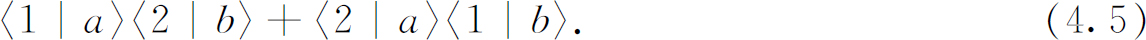
在计数器中得到一对粒子的概率就是这个振幅绝对值的平方，
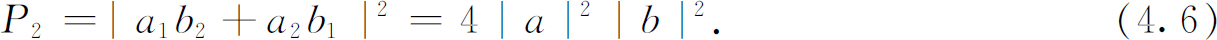
我们得到这样的结果：两个全同玻色子被散射到同一状态的概率是假设两个粒子不相同时所计算出的概率的两倍 。
虽然我们刚才考虑两个粒子在不同的计数器中被观察到，我们在下面就会知道，这并不是实质性的。我们设想沿1和2两个方向的粒子都进入放在某一距离处的一个单独的小型计数器中。我们定义方向1为正对着计数器上面积元dS 1 的方向，方向2正对着计数器的面积元dS 2 。（我们设想计数器有一和散射线垂直的面。）现在我们不可能给出粒子将进入某一精确方向或到达空间某一特定点 的概率。这种事是办不到的——进入任一精确方向的机会为零。如果我们希望说得非常具体的话，我们必须这样定义我们的振幅，它给出到达计数器上单位面积 的概率。假定我们只有粒子a ，它具有被散射到方向1的某个振幅。我们定义〈1|a 〉＝a 1 是a 被散射到在方向1的计数器单位面积 上的振幅。换言之，a 1 的标度已选定了——我们说它已被“归一化”，于是粒子a 被散射到面积元 dS 1 上的概率是
如果我们的计数器的总面积是ΔS ，我们使dS 1 遍及这个面积的范围，粒子a 被散射到计数器中的总概率是：
和以前一样，我们假设计数器足够小，以致振幅a 1 在计数器的整个面上没有显著的变化，那么a 1 是一个常数振幅，我们可称它为a 。于是粒子a 被散射到计数器中某处的概率是
用同样的方法，我们得到粒子b ——单独存在时——被散射到某一面积元dS 2 的概率是
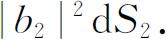
（我们用dS 2 代替dS 1 ，因为下面我们要使a 和b 进入不同的方向。）我们再使b 2 等于常数振幅b ，于是粒子b 在探测器中被计数的概率是：
现在当两个粒子同时存在时，a 被散射到dS 1 而b 被散射到dS 2 的概率是
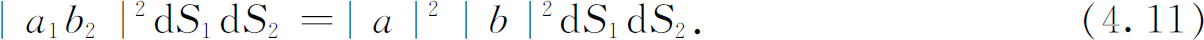
如果我们要求的是 a 和b 两者都 进入计数器的概率，我们将dS 1 和dS 2 都在ΔS 上积分，得到
附带提一下，我们注意到它正好等于pa ·pb ，正如你们假定粒子a 和b 互相独立地行动那样。
然而，如果两个粒子是全同的，对于每一对面积元dS 1 和dS 2 就有两个不能区别的概率。粒子a 进入dS 1 而粒子b 进入dS 2 和粒子a 进入dS 2 而粒子b 进入dS 1 是不能区别的，所以这两个过程的概率将相互干涉。（在上面当我们有两个不同的 粒子时——虽然事实上 我们并不在乎到底哪一个粒子跑到计数器的哪一部分——原则 上我们能够找出哪个粒子进入哪里，所以不存在干涉。而对于全同粒子，即使在原则上我们也不可能断定。）于是，我们必须把两个全同粒子到达dS 1 和dS 2 的概率写成
然而，现在我们对计数器的面积求积分时，我们必须小心。如果令dS 1 和dS 2 都遍及整个面积ΔS ，我们就把面积上每一部分都计算了两次 ，因为式（4.13）包括了任何一对面积元dS 1 和dS 2 (1) 可能会遇到的所有情况。如果我们把结果除以2来改正双重计算，我们仍然可以求这个积分。于是，对于全同玻色子，我们得到
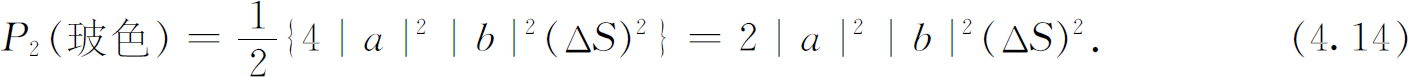
这正好又等于式（4.12）的两倍，该式是我们对可以区别的粒子求得的。
如果我们设想一下，我们知道通道b
已经将其粒子送入某一特定方向，我们可以说第二个粒子进入同一方向的概率等于我们把它当作独立事件计算时所预期的结果的两倍。玻色子具有这样的特性：如果已有一个粒子处于某一状态，在这同一状态中出现第二个粒子的概率
等于第一个粒子不在这个状态时的两倍。这个事实常常用下面的方式来表达：如果已有一个玻色子处于一给定的状态中，再将另一全同玻色子放进这同一状态的振幅等于第一个粒子不在该状态时的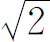
倍。（从我们所采用的物理的观点来看，这并不是表达这个结果的适当方式，但是如果始终将它当作一个法则来使用，它肯定会给出正确的结果。）
我们把上一节的结果推广到具有n 个粒子的情况。设想图4-4所示的情况。我们有n 个粒子a ，b ，c ，…它们分别被散射至1，2，3，…，n 等各个方向上。所有这n 个方向都正对着放在远处的一个小计数器。和上一节一样，我们把所有的振幅都归一化，各个粒子单独行动时进入计数器上面积元dS 的概率是：
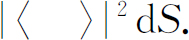
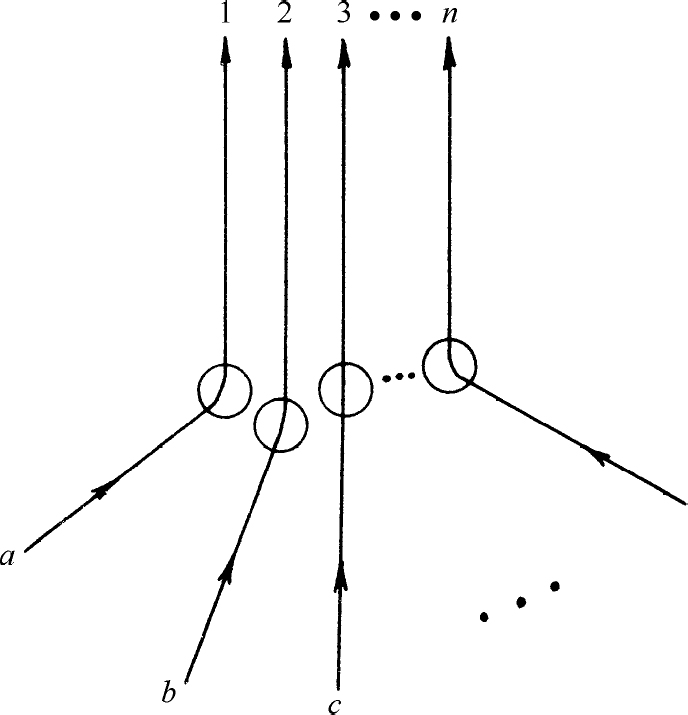
图4-4 n 个粒子被散射到靠近的终态
让我们先假设这些粒子都是可以区别的，于是，n 个粒子在n 个不同的面积元上都一起被计数的概率是：
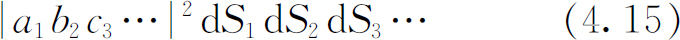
我们再假设振幅不依赖于dS 在计数器（假设它很小）上的位置，并把这些振幅称为a ，b ，c ，…。概率式（4.15）变成：
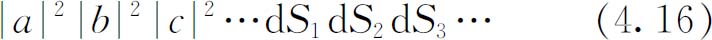
将各个dS 分别在计数器的表面ΔS 上求积分，我们得到同时对n 个不同粒子计数的概率P n （不同）为
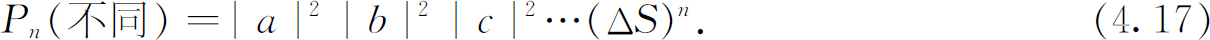
这正好等于各个粒子分别进入计数器的概率的乘积。它们各自独立地行动——某一粒子进入计数器的概率与另外还有多少其他粒子也进入计数器无关。
现在假设所有的粒子都是全同的玻色子。对于每一组方向：1，2，3，…有许多不可分辨的可能性。例如，当只有3个粒子时，我们有下列几种可能性：
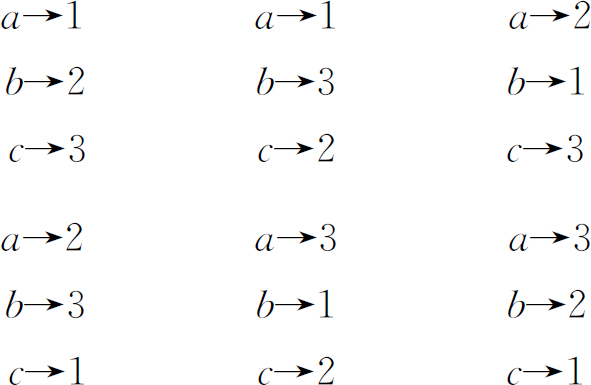
共有6种不同的组合。n 个粒子就有n ！种不同的、但是不可分辨的可能性，因此我们必须把它们的振幅相加。于是，n 个粒子在n 个面积元上计数的概率就是
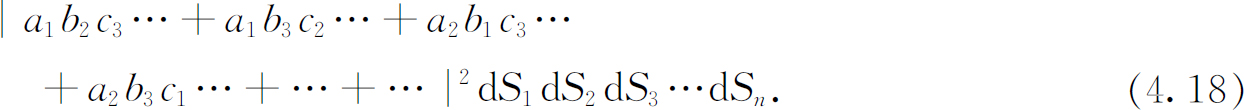
我们再次假设所有的方向很靠近，因而我们可以设
，对于b
，c
，…也如此，式（4.18）表示的概率则成为：
当我们把各个dS 对计数器的面积ΔS 求积分时，每个可能的面积元的乘积都计算了n ！次，对此我们除以n ！来加以修正，于是得到
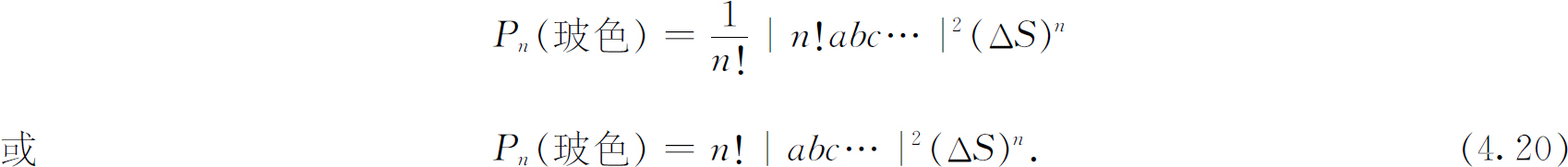
把这个结果和式（4.17）比较，我们看到，对n 个玻色子一起计数的概率比假设这些粒子都是可以分辨的情况下所算出的概率大n ！倍。我们可以把以上结果概括为
于是，玻色子情况的概率比假设粒子都独立行动所算出的概率大n ！倍。
下面的问题可使我们更好地看出上述结果的意义：一个玻色子进入已有n 个其他 玻色子存在的某个特殊状态的概率是什么？我们把这个新加入的粒子叫做ω 。包括ω 在内，我们共有（n ＋1）个粒子，式（4.20）变成
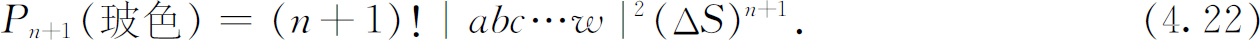
此式可以写成
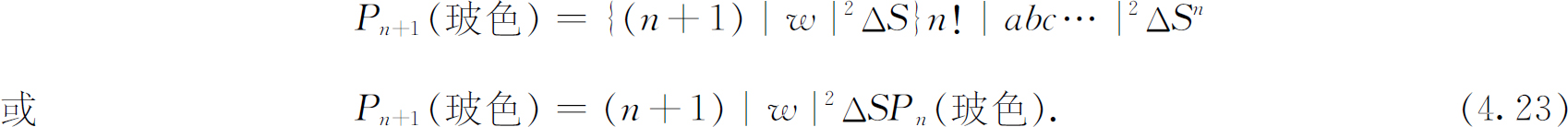
我们可以下列方式来看待这个结果。|ω |2 ΔS 是当没有其他粒子存在时，粒子ω 进入探测器的概率，P n （玻色）是已经有了另外n 个玻色子存在时的概率。所以式（4.23）表明，当已经有 另外的n 个全同玻色子存在于某一状态中时，在这同一个状态中再增加一个 玻色子的概率增强了 （n ＋1）倍。由于其他粒子的存在 ，使得再加入一个粒子的概率增大了。
在上面的整个讨论中，我们所谈的都是像α 粒子散射这一类的过程。但这并不是本质问题。我们可以谈论粒子的产生，例如光的发射。发射光时，光子“产生”了。在这样的情况中，我们不需要图4-4中的入射线。我们只要考虑有一些原子发射n 个光子，如图4-5所示。于是，我们的结果也可以表述为：如果在某一特定的状态中已经有了n 个光子，原子再发射一个光子到这个特定状态中的概率增大了（n ＋1）倍 。
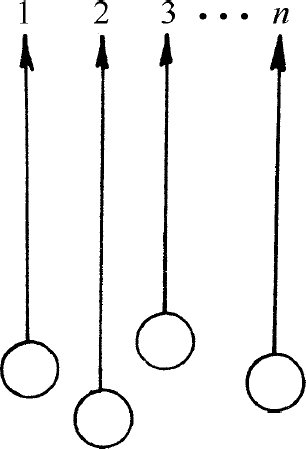
图4-5 处于接近状态中的n 个光子的产生
人们常常喜欢把这个结果概括为：当已有n
个光子存在时，再发射一个光子的振幅
增大了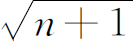
倍。当然，这只是同一事情的另一种说法而已，因为振幅的平方就是概率。
从任何一个状态φ 转变到另一个状态χ 的振幅就是从状态χ 变为状态φ 的振幅的共轭复数：
这在量子力学中是普遍正确的。不久我们将学习这个定律，但目前我们就假定它是正确的。我们可以用它来弄清楚光子是怎样从一个给定的状态被散射或吸收的。一个光子加入某一个已经有n 个光子存在于其中的状态（譬如说i ）的振幅是
其中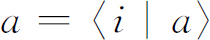
是没有其他粒子存在时的振幅。应用式（4.24），过程反方向进行——从（n
＋1）个光子变为n
个光子——的振幅是
这不是通常所用的叙述方式。人们不喜欢考虑从（n ＋1）到n 这样的过程，而总喜欢从存在n 个粒子的状态开始。于是，他们说：当有n 个光子存在时，从其中吸收掉一个光子的振幅——换言之，从n 到n－1 ——是
当然这和式（4.26）完全一样。但这样却有要努力记住何时用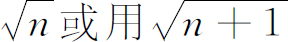
的麻烦。这里有一个记忆的方法，a
前面的因子总是出现的最大光子数的平方根，不论此数出现在反应前，还是反应后，式（4.25）和（4.26）表明这个定律实际上是对称的——只有当你们把它写成式（4.27）的形式，看上去才不对称。
从这些新的法则可以推导出许多物理的结论；我们说一下其中一个与光的发射有关的结论。假如我们设想这样一种情况，光子被包围在一个盒子里面——你们可以想象一个用反射镜做墙的盒子。现在假定在这个盒子中有n 个光子，它们都处于同样的状态——同样的频率、同样的传播方向和偏振——所以它们是不可分辨的。此外在盒子中还有一个原子，它可把另一个光子发射到这同一状态中。这个原子发射光子的概率是
它吸收一个光子的概率是
其中|a |2 是原来没有光子存在时，这个原子发射一个光子的概率。我们已经在第1卷第42章中以稍许不同的方式讨论过这些法则。式（4.29）说明原子吸收一个光子并跃迁到较高的能量状态的概率正比于照射到这个原子上的光的强度。但是，正如爱因斯坦首先指出的，原子向下 跃迁到较低能量状态的概率包含两个部分，这个概率等于自发跃迁的概率|a |2 加上感应跃迁的概率，后者正比于光的强度——即正比于出现的光子数目，即n |a |2 。此外，正如爱因斯坦所说的，吸收系数和感应发射系数相等并与自发发射的概率有关。我们这里所学到的是：如果用出现的光子的数目（用它来代替每单位时间通过每单位面积的能量）来量度光的强度，吸收、感应发射以及自发发射的系数都相等。这就是第1卷第42章式（42.18）中的爱因斯坦系数A 和B 之间关系的实质。
我们要应用关于玻色子的法则再来讨论黑体辐射的光谱（见第1卷第42章）。我们要找出在一个盒子内部，辐射与某些原子处于热平衡状态时，该盒子里面有多少光子。假设对于光的每一种频率ω
，存在着某一数量N的原子，这些原子具有两个能量状态，其能量间隔为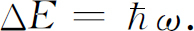
参见图4-6。我们把较低的能量状态叫做“基”态，较高能量的状态叫做“激发”态。令Ng
和Ne
分别是基态和激发态上的原子平均数，那么，当这些原子处于温度为T
的热平衡状态时，由统计力学，我们有
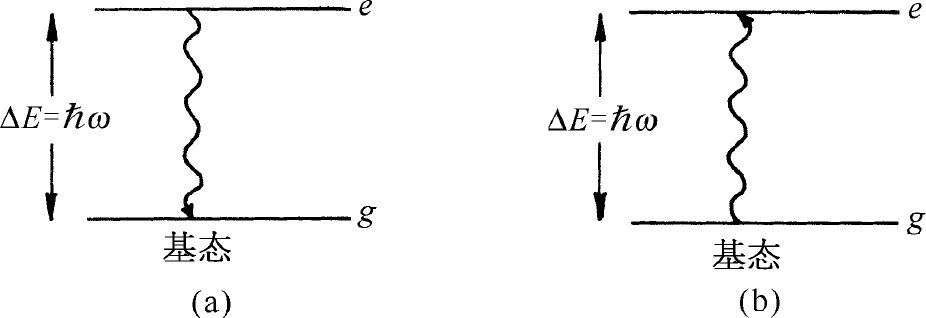
图4-6 频率为ω 的光子的辐射和吸收
处于基态的每一个原子都可以吸收一个光子并跃迁到激发态，激发态的每一个原子都可以发射一个光子并跃迁到基态。平衡状态下，这两个过程的速率必定相等。这速率正比于事件的概率和其中原子的数目，设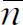
是处于频率为ω
的状态中的光子的平均数。那么，从该状态中吸收的吸收率是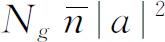
，光子发射到这个状态中的发射率是
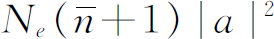。令这两个速率相等，我们就有
把此式和式（4.30）结合起来，我们得到
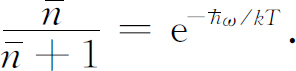
解出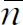
，得到
这是在热平衡的空腔中，处于频率为ω
的状态中光子平均数。因为每一个光子具有能量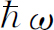
，在这个状态中光子的总能量是
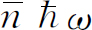，或
附带提一下，此式和另外一章中的一个式子［第1卷第41章式（41.15）］相同。你们还记得，对于任何一种谐振子——例如弹簧上的重物——量子力学能级是以相等的间距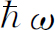
均匀地分布的，如图4-7所示。如果我们令第n
个能级的能量为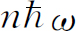
，我们发现，这样的振子的平均能量也由式（4.33）表示。然而这个方程在这里是通过计算粒子数对光子导出的，它也得出同样的结果，这是量子力学不可思议的奇迹之一。如果我们从考虑没有相互作用的玻色子的某种状态或条件开始（我们曾经假设光子彼此之间是没有相互作用的），然后设想在这个状态中可以放入或者零个、或者一个、或者两个……直到任意数目n
个粒子。人们发现，这个系统所有量子力学意义上的行为与谐振子完全一样。所谓谐振子是指一种动力学系统，譬如像弹簧上的重物或者共振腔里的驻波。这就是为什么可以用光子来描绘电磁场的理由。从某种观点来看，我们可以用大量的谐振子这一思想来分析盒子或空腔中的电磁场。根据量子力学把每一种振动模式当作一种谐振子。从另一种观点来看，我们可以对同样的物理过程，按照全同玻色子的概念来进行分析。两种方式所得出的结果总是完全一致
。你们无法决定电磁场实际上应当用量子化的谐振子来描写还是用在各个状态中的光子数来说明，可以证明这两种观点在数学上是完全相同的。所以今后我们可以说盒子里处于某一特定状态的光子数目，也可以说和电磁场某一特定振动模式相联系的能级的数目。它们是描述同一事物的两种不同的方式。对于自由空间中的光子，这也同样正确，它们相当于器壁移至无穷远处的空腔中的振动。
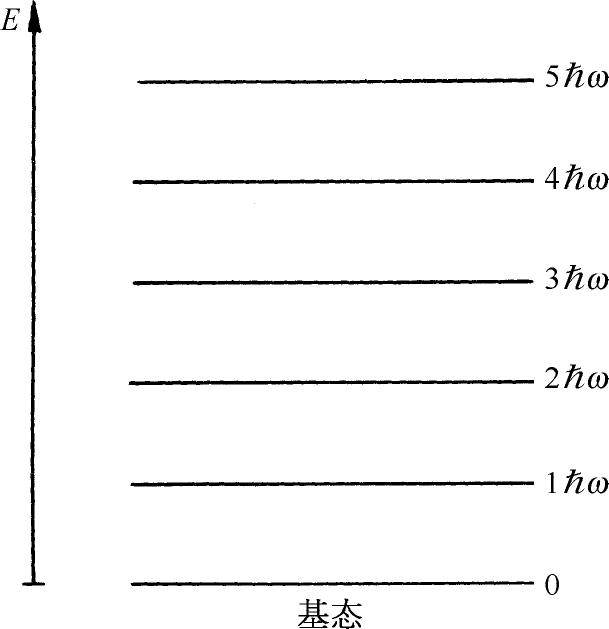
图4-7 谐振子的能级
我们已算出在温度为T 的盒子里任一特定的模式的平均能量。为得到黑体辐射定律，我们只需再知道一件事，即需要知道在每一种能量状态有多少模式。（我们假设，对于每一种模式，在盒子里——或者在器壁上——都有一些原子，它们具有可能辐射到这个模式的能级，从而每一模式都能达到热平衡。）黑体辐射定律的表达通常是给出：在单位体积内，在微小的频率间隔ω 到ω ＋Δω 中的光所携带的能量。所以我们需要知道盒子内部，在频率间隔Δω 中有多少个模式。虽然这个问题在量子力学中经常出现，但它纯粹是一个关于驻波的经典问题。
我们只对矩形盒子求解。对于任意形状的盒子，结果都是相同的。但是对于任意情况，计算非常复杂。而且我们只对线度比光的波长大得多的盒子有兴趣。这样就有亿万个模式。在任意小的频率间隔Δω 内也有许多模式。所以我们可以讨论频率ω 处，任何频率间隔Δω 中的“平均数”。首先我们讨论在一维情况——就像在一条紧绷着的绳子上的波——中有多少个模式。你们都知道，每一种模式就是一个正弦波，在两个端点处必须趋于零。换言之，整个线的长度必须为整数个半波长，如图4-8所示。我们喜欢用波数：k ＝2π /λ 。令kj 为第j 个模式的波数，我们有：
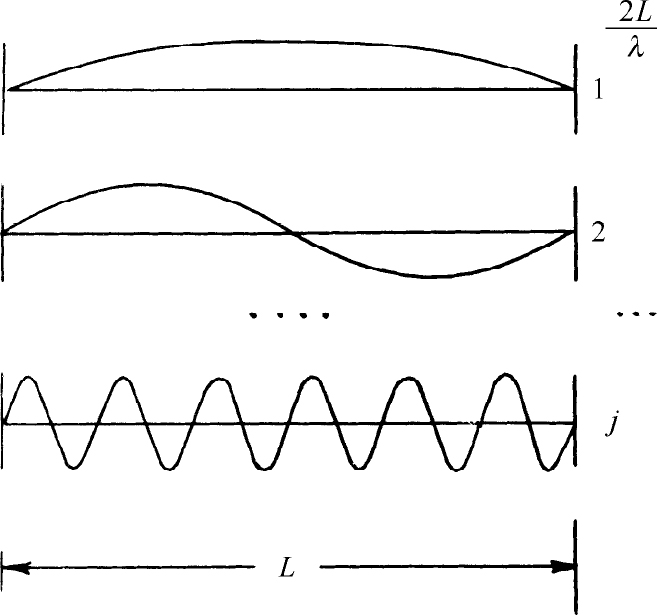
图4-8 一条线上驻波的模式
其中j 是任意整数。相邻的模式的波数间隔δk 是
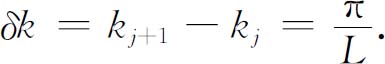
我们假设kL
如此之大，从而在很小的间隔Δk
内就有许多模式。令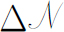
为间隔Δk
内模式的数目，我们有：
现在，在量子力学方面工作的理论物理学家常常喜欢用只有这个数目一半的模式数来表示。他们写作
我们来解释一下这是为什么，他们通常喜欢用行波的概念来思考——某些波向右行进（具有正的k
），某些波向左行进（具有负的k
）。但是，所谓“模式”是对于驻波
而言的。驻波是两列波之和，两列波各自在相反方向上行进。换言之，他们认为每一驻波包含了两个不同的光子“态”。如果人们喜欢用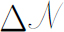
来表示给定k
（现在k
的范围包括从正的到负的数值）的光子态的数目，那么应该取式（4.35）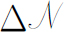
的一半大小。（现在所有的积分必须从k
＝－∞积到k
＝＋∞，从而对于任何给定k
的绝对值算出的状态总数仍然完全正确。）当然，这样并没有很好地描写驻波，但是我们用前后一贯的方法来计算振动模式。
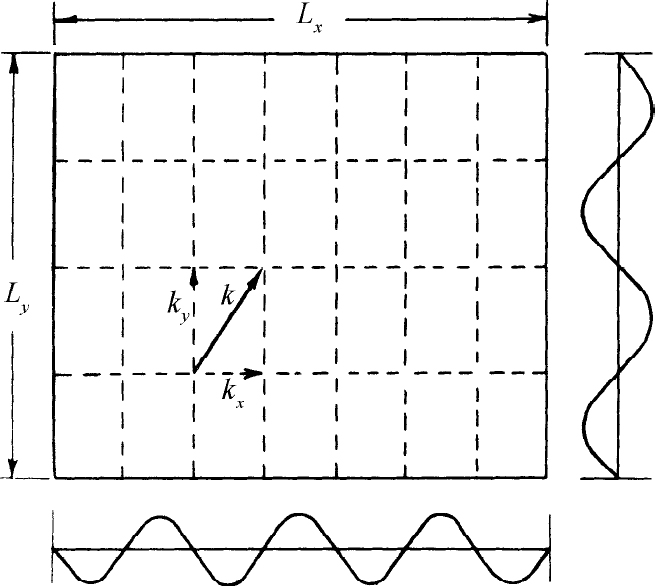
图4-9 二维的驻波模式
现在我们要把结果推广到三维情况。矩形盒子里的驻波必须沿着每一个轴 都有整数个半波长。图4-9所示是其中的二维情况。每个波的方向和频率都用一个波矢k 来表示。波矢的x ，y 和z 方向的分量必定满足类似于式（4.34）那样的方程。所以我们得到
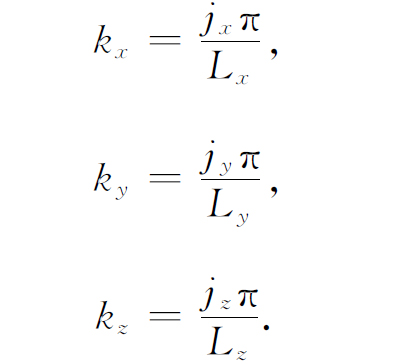
和前面一样，具有kx 值在间隔Δkx 内的模式数为
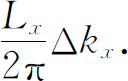
对于Δky
和Δkz
的情况也是一样。令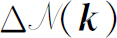
为波矢k
的模式的数目，波矢k
的x
分量在kx
和kx
＋Δkx
之间，它的y
分量在ky
和ky
＋Δky
之间，它的z
分量在kz
和kz
＋Δkz
之间。那么
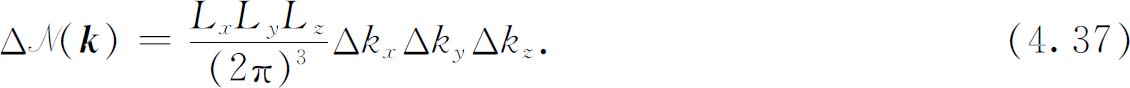
乘积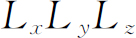
等于盒子的体积。于是我们得到一个极其重要的结果：对于高的频率（波长比盒子的线度小得多），空腔中模式的数目正比于盒子的体积V
和“k
空间中的体积”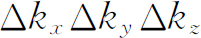
。这个结果在许多问题中反复地出现，应该将它记住：
虽然我们还没有证明过，但这个结果不依赖于盒子的形状。
我们现在应用这个结果来求光子的频率范围Δω 内的光子模式的数目。我们有兴趣的只是各个模式中的能量——对波的方向不感兴趣，我们想要知道在给定频率范围内模式的数目。真空中k 的大小和频率的关系是
所以在频率间隔Δω 内，与波矢k 相对应的模式就是与大小在k 到k ＋Δk 之间的全部模式，它们与方向无关。在k 到k ＋Δk 之间的“k 空间体积”是一球壳，其体积为
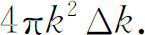
于是模式的数目为
然而，由于我们现在感兴趣的是频率，我们应将k ＝ω /c 代入上式，于是得到
这里还有一个复杂的情况。如果我们讨论的是电磁波的模式，对于任一波矢k 可以有两个（互相正交的）偏振。因为这些模式是互相独立的，我们必须——对于光——把模式的数目加倍。所以我们得到
我们曾经指出，式（4.33）每一模式（或每一“状态”）的平均能量是
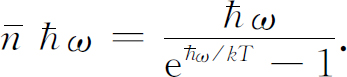
将此式乘以模式的数目，我们就得到在区间Δω 内这些模式的总能量ΔE ：
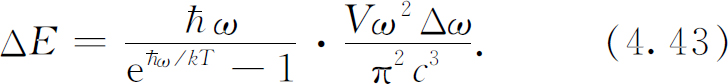
这就是关于黑体辐射频谱的定律，我们在第1卷第41章中已经得到过这一定律。其频率谱画在图4-10中。你们现在看到，这个答案取决于光子是玻色子这一事实，它们具有使所有的粒子都进入同一状态的倾向（因为这样做振幅大）。你们要记住，是普朗克对黑体辐射光谱的研究（从经典物理学看来，这是很神秘的问题），以及他对式（4.43）的发现开创了量子力学整个学科。
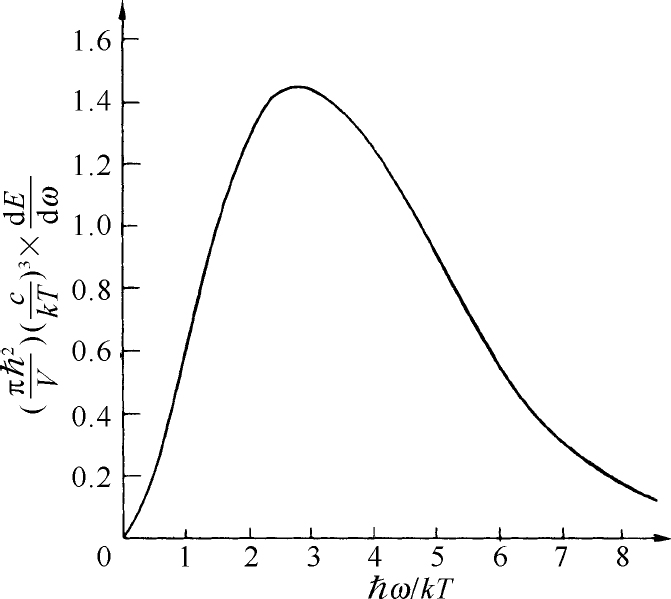
图4-10 处于热平衡的空腔中辐射的频谱，“黑体”光谱
液氦在低温下有许多奇特的性质，遗憾的是我们现在不可能花时间来详细叙述，但它的许多性质起源于氦原子是玻色子这个事实。其中一个性质是，液氦在流动时没有任何黏性阻力。实际上，这就是我们在以前有一章中所讲的理想“干”水——假如速度足够低的话。其原因如下：为使液体具有黏性，就必定有内能损失；必须有某种方法使一部分液体具有与其余部分不同的运动。这就意味着必须有可能把某些原子撞击到不同于另一些原子所占据的状态中去。但是在足够低的温度下，当热运动变得非常小时，所有的原子都企图进入同样的状态中。于是，只要有一部分原子在向前运动，所有的原子都要以同样的方式一起运动。这种运动具有一种刚性，并且很难使它像在互相独立的粒子中所发生的那样分裂为不规则的湍流。所以在玻色子组成的液体中，所有原子有极强的进入同样状态的倾向——这个倾向可以用我们以前求得的因子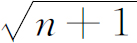
来表征。（对于一瓶液氦来说，n
当然是一个非常大的数字！）在高温下，这种合作运动不出现，因为这时有足够的热能使不同的原子进入不同的高能态。但是在足够低的温度下，突然在某一瞬间所有的氦原子都试图进入同一状态中。氦就成为超流体。顺便提一下，这个现象只出现在原子量为4的氦同位素中。对于原子量为3的氦同位素，各个原子都是费米子，其液体是正常的液体。由于超流动性只发生于He4
，这显然是一种量子力学的效应——由于α
粒子的玻色子性质。
费米子的行为完全不同。我们来看一下，如果试图把两个费米子放到同一状态中将会发生些什么。我们回到原先的例子，求两个全同费米子被散射到几乎完全相同的方向上的振幅。粒子a 进入方向1而粒子b 进入方向2的振幅是
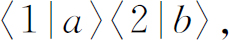
两个粒子出射方向互相交换的振幅是
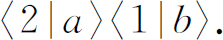
因为我们讨论的是费米子，这个过程的振幅等于这两个振幅之差：
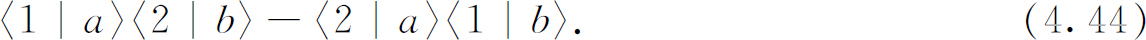
我们所说的“方向1”不仅表示粒子的某一个运动方向，还表示其确定的自旋方向。“方向2”和方向1几乎完全相同，并且相当于同样的 自旋方向。于是〈1|a 〉和〈2|a 〉近乎相等。（如果出射状态1和2的自旋不相同，这个结果就不一定成立，因为有某些理由可以说明为什么振幅要依赖于自旋方向。）现在如果使方向1和2互相靠近，式（4.44）中的总振幅就变成零。对于费米子所得出的结果比玻色子简单得多。两个费米子——譬如两个电子——根本不可能进入完全相同的状态。你们永远不会发现两个自旋方向相同的电子在同一个位置上。两个电子不可能具有相同的动量和相同的自旋方向。如果它们在同一位置上或具有同样的运动状态，唯一的可能性是它们必须有相反的自旋。
这有些什么后果呢？有许多十分引人注目的效应，这些效应都归结为一个事实：即两个费米子不可能同时进入同一状态。实际上，几乎物质世界的所有特性都和这个奇妙的事实有关。周期表所显示的丰富多样的元素基本上就是这一法则的结果。
当然，我们无法说出如果这个法则发生了变化，世界将要成为什么样子。因为它是量子力学的整个结构的一个部分，我们不可能说清楚如果关于费米子的法则改变了，还有别的什么东西会改变。不管怎样，让我们试着看一下，假如只有这个法则改变的话，可能会发生些什么。首先，我们可以证明，这样一来所有的原子就会多少有点相同了。我们从氢原子开始吧，它不会受到明显的影响。构成原子核的质子被球对称的电子云所包围，如图4-11（a）所示。正如我们在第2章中所描述的那样，电子被吸向中心，但不确定性原理要求在空间的密集和动量的集中之间有一个平衡。这个平衡意味着必定存在着某一能量和某种弥散状态的电子分布，这种分布决定了氢原子的特征线度。
图4-11 假如电子的行为像玻色子，原子看上去可能会是什么样的
现在假定我们有一带两个单位电荷的原子核，譬如氦原子核。这个原子核要吸引两个电子，如果电子是玻色子，它们就会——除了它们之间的排斥作用外——尽可能地一齐挤向原子核。氦原子看上去就会像图4-11（b）所画的那样。同样，锂原子具有3个荷电核子，它的电子分布如图4-11（c）所示。各种原子看上去多少是相同的——一个所有电子都处在原子核附近的小圆球，没有方向性，也并不复杂。
然而，由于电子是费米子，实际情况就大不相同了。对于氢原子来说，情况基本不变。唯一的差别是电子具有自旋，这在图4-12（a）中用一个小箭头表示。然而就氦原子而言，我们不能再把两个电子紧靠在一起。不过且慢，这只在两者的自旋相同时才是正确的。如果两个电子的自旋相反，它们就可以 占据同一状态。所以氦原子看上去也没有很大的不同。它看上去像图4-12（b）所画的那样。然而对于锂来说，情况就变得完全不同了。我们可以把第三个电子放在什么地方呢？第三个电子不能再和另外两个电子紧靠在一起了，因为这一状态上的两个自旋方向都已被占据了。（你们记得，一个电子或任何一个自旋为1/2的粒子只有两个可能的自旋方向。）第三个电子不能靠近另外两个电子所占据的地方，所以，它只能在远离原子核的另一个状态中占据一个特殊位置，见图4-12（c）。（这只是一种极其粗浅的说法，因为实际上这3个电子都是全同的。由于我们不能真正区别这个电子和那个电子，所以我们的图像只是近似的。）
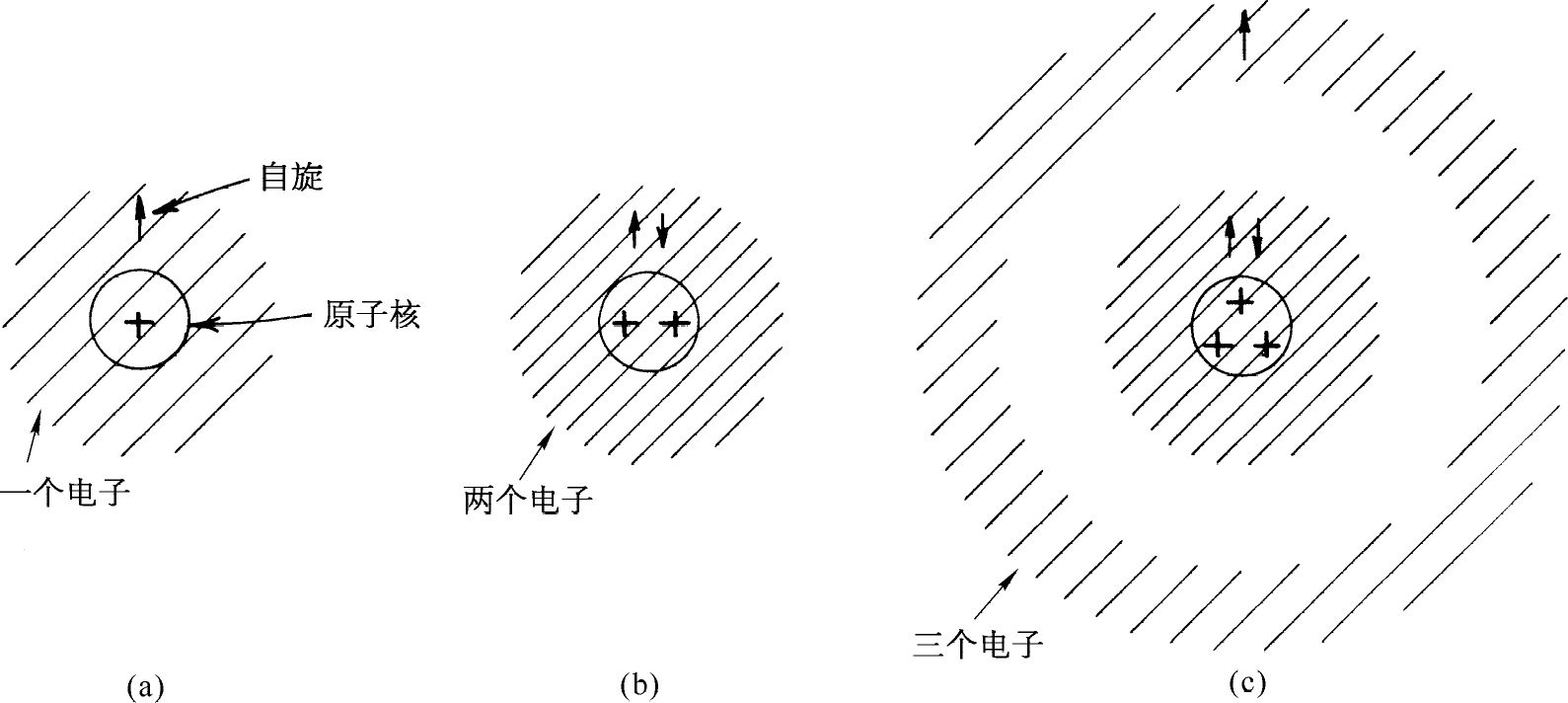
图4-12 真实的费米型的、自旋为1/2的电子的原子组态
现在我们可以理解为什么不同的原子具有不同的化学性质。因为锂原子中的第三个电子离中心较远，相对地说对它的束缚比较松。从锂原子中拿走一个电子比从氦原子中拿走一个电子来得容易。（实验得到，使氦电离需要25V，而使锂电离只要5V。）这就说明了锂原子的价键。价键的方向性和外层电子的波的图样有关，我们暂时不去讨论它。但是我们已经能够看出所谓不相容原理 ——不可能在完全相同的状态（包括自旋）中找到两个电子——的重要性。
不相容原理对大尺度物体的稳定性也起着作用。我们以前曾经说物质中各个原子之所以不会坍缩是由于不确定关系，但是这不能解释为什么不能随心所欲地把两个氢原子紧紧挤压在一起——为什么所有的质子不能互相靠得很近，使一大团电子围绕着它们。答案当然是由于没有两个以上的电子——具有相反的自旋——可以大体上处在同一个位置上，氢原子之间必须保持一定的距离。所以，大尺度的物质的稳定性实际上是电子的费米子性质的结果。
当然，如果两个原子的外层电子具有相反方向的自旋，它们就能够彼此接近。实际上化学键正是这样发生的。结果是，如果两个原子之间有一个电子，则这两个原子总共具有最低能量。对两个带正电的原子核来说，这时受到的是一种指向中间的电子的静电吸引力。只要两个电子的自旋相反，就可将它们放在两个原子核的中间。最强的化学键就是这样产生的。没有比这更强的链联了，因为不相容原理不允许在两个原子之间的空间里存在着两个以上的电子。我们认为氢分子看上去多少有些像图4-13所示的那样。
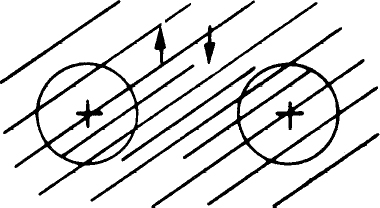
图4-13 氢分子
我们还要讲一个不相容原理的结果。你们记得如果氦原子中的两个电子都靠近原子核，那么它们的自旋必须相反。现在假定我们设法把两个电子的自旋排列在同一个方向上——我们可以设想加上一个极强的磁场使电子的自旋排成同一方向。但是，这样一来，两个电子就不可能占据空间的同一状态，其中一个电子必须占据一个不同的几何位置，如图4-14所示。离原子核较远的那个电子具有较小的结合能。于是整个原子的能量就变得更大得多。换言之，当两个电子的自旋方向相反时，总的吸引力要强得多。
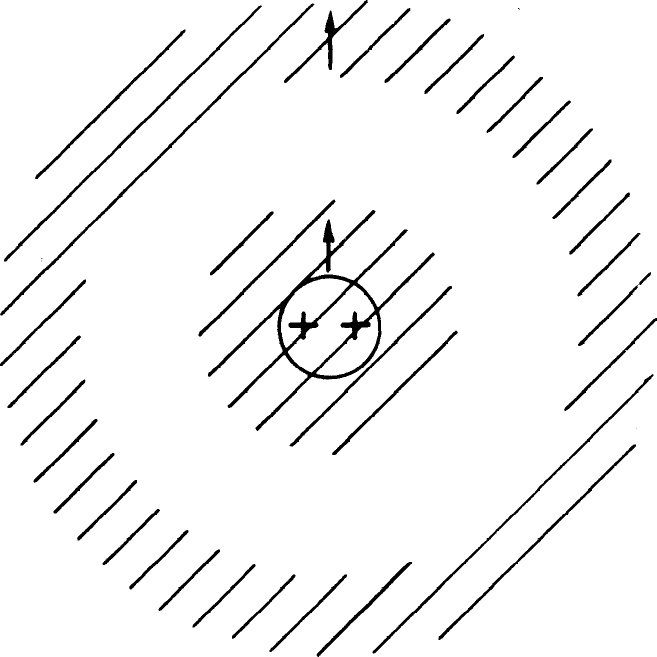
图4-14 一个电子在高能态的氦
所以，当两个电子接近时，有一个表观上的、巨大的力试图使自旋按彼此相反的方向排列，如果两个电子试图进入同一位置，其自旋就有极其强烈的反向排列倾向。这一试图使两个自旋取向相反的表观上的力比起电子磁矩之间的微弱的力来要强得多。你们记得，在我们讲到铁磁性的时候，曾经有过这样一个不可思议的问题，为什么不同的原子中的电子具有极强的平行排列的倾向。对此虽然还没有定量的解释，但可认为其中所发生的过程是这样的：原子的内层电子和已经变为在整个晶体内自由运动的外层电子因不相容原理而相互作用，这种相互作用使得自由电子的自旋和内层电子的自旋的取向相反。但是只有当所有的内层电子都具有相同的自旋方向时，自由电子和内层电子的自旋才可能相反，如图4-15所示。看来可能是这样的情况：不相容原理的效应通过自由电子间接地起作用，引起了在铁磁体中起作用的强烈的排列力。
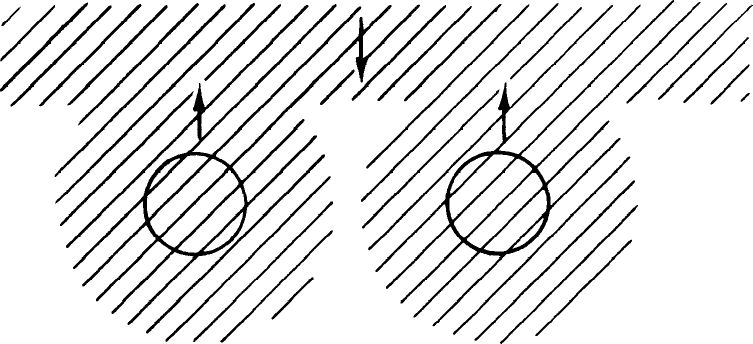
图4-15 在铁磁体晶体中可能的机理；传导电子反平行于不成对的内层电子
我们再讲一个受不相容原理影响的例子。以前曾经讲过，中子和质子之间、质子和质子之间、中子和中子之间的核力都是相同的。为什么一个质子和一个中子可以粘在一起形成一个氘原子核，而不存在只有两个质子或者只有两个中子的原子核呢？事实上，氘原子核大约受到2.2MeV的能量束缚，然而在一对质子之间却没有相应的束缚以组成原子量为2的氦同位素。这样的核不存在，两个质子的组合不形成束缚态。
这个问题的答案是两个效应的共同结果：第一是由于不相容原理，第二是由于核力对于自旋方向比较敏感这一事实。中子和质子之间的作用力是吸引力，而且这种力当它们的自旋相互平行时比它们的自旋相反时稍微强一些。由于两种力的这一点差别，使得中子和质子的自旋方向互相平行时，正好足以构成氘原子核；当它们的自旋方向相反时，质子和中子间的引力不足以使它们束缚在一起。由于中子和质子的自旋都是1/2，而且在同样的方向上，因此氘原子核的自旋为1。然而我们知道，两个自旋互相平行的质子不可能紧挨在一起。如果不是由于不相容原理，两个质子就可以束缚在一起。但是由于自旋方向相同的质子不可能在同一位置存在，因此He2 原子核就不存在。两个质子如果其自旋相反就可能聚集在一起，但这样就没有足够的束缚力以形成稳定的原子核，因为自旋相反时的核力太弱了，不足以把一对核子束缚在一起。自旋相反的中子和质子之间的相互吸引力可以从散射实验中观察到。对两个自旋平行的质子所做的同样的散射实验表明也存在着相应的吸引力。所以不相容原理解释了为什么氘可以存在而He2 却不能。
————————————————————
(1) 在式（4.11）中，交换dS 1 和dS 2 就得到另一个不同的事件，所以两个面积元都必须遍及计数器的整个面积。在式（4.13）中，我们把dS 1 和dS 2 成对地处理，并且包括了可能发生的所有情况。如果积分又包含dS 1 和dS 2 交换后所发生的情况，各种情况就计算了两次。